5 Дерева. Алгоритми побудови остовного дерева

5.1 Мета заняття

Ознайомлення на практичних прикладах з поняттям «дерево», з основними властивостями дерев та їх видами. Вивчення способів перелічення графів і дерев. Ознайомлення з основними алгоритмами побудови дерев. Вивчення алгоритму побудови остовного дерева пошуком у глибину.

5.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-8, 10-12] з таких питань: визначення дерева; властивості дерев; перелічення графів і дерев (неізоморфних, кореневих, позначених); використання теорії перелічення конфігурацій, що створена Д. Пойа, при обчисленні кількості неізоморфних графів; використання формули А. Келі для підрахування числа позначених дерев звершинами; остови графа, перелічення остовів для повного (простого) графа; перелічення остовів графа у загальному випадку (теорема Кірхгофа); алгоритм побудови остовного дерева (пошук у глибину); алгоритм побудови остовного дерева шляхом довільного перегляду ребер; алгоритми побудови остова мінімальної ваги (алгоритм Дж. Краскала, алгоритм Р. Прима); орієнтовані та бінарні дерева; правила обходу бінарних дерев; правило побудови бінарного дерева з будь-якого дерева.

Підготовка і виконання практичного заняття проводиться у два етапи. Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: дерево; центр дерева; ліс; позначений граф; однакові позначені графи; кількість неорієнтованих, простих, позначених графів; число неізоморфних (простих, неорієнтованих) графів без позначок; число позначених дерев; число звичайних (неізоморфних) дерев з вершинами; корінь дерева; кореневе дерево; остовний підграф (остов, каркас графа); матриця Кірхгофа простого графа; зважений граф; остів мінімальної ваги; вага підграфа; орієнтоване дерево; нащадок вершини; предок вершини; «батько» для вершини; «син» для вершини; лист; глибина вершини; висота вершини; висота дерева; рівень вершини; упорядковане дерево; бінарне (двійкове) дерево; ліве піддерево; праве піддерево; еквівалентне бінарне дерево.

Під час виконання першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень. Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які представлено у підрозділі 5.3, на основі запропонованих типових прикладів (див. підрозділ 5.4).

5.3 Контрольні запитання і завдання

5.3.1 Контрольні запитання

1. Який граф називається деревом? Наведіть приклади дерев.

2. Що називається лісом у теорії графів?

3. Перелічить основні властивості дерев.

4. Який граф називається позначеним?

5. Які два позначених графа не різняться (є однаковими)?

6. Якою формулою можна скористатися для визначення кількості неорієнтованих позначених простих графів з вершинами таребрами?

7. Якою формулою можна скористатися для визначення кількості неізоморфних позначених дерев?

8. Як визначити число неізоморфних графів без позначок?

9. У яких випадках використовується формула А. Кэли? Наведіть цю формулу.

10. Дайте визначення остова (каркаса) графа.

11. Приведіть приклад складання матриці Кірхгофа простого графа.

12. Для розв’язання яких задач використовується теорема Кірхгофа?

13. Перелічить основні алгоритми побудови остовів графа.

14. Наведіть алгоритм Дж. Краскала для побудови остова мінімальної ваги.

15. Дайте визначення орієнтованих і бінарних дерев.

16. Охарактеризуйте способи обходу бінарного дерева.

17. Поясніть правило побудови бінарного дерева з будь-якого дерева.

5.3.2 Контрольні завдання

Завдання 1. Підрахувати кількість позначених неорієнтованих простих графів з вершинамиі ребрами танарисувати декілька з таких графів.

Завдання 2. Підрахувати кількість усіх позначених неорієнтованих простих графів з вершинами танарисувати ці графи.

Завдання 3. Підрахувати кількість усіх позначених неорієнтованих простих графів з вершинами танарисувати тільки ті графи, у яких кількість ребер дорівнює чотирьом.

Завдання 4. Записати простий дріб такого виду , де– кількість усіх позначених неорієнтованих простих графів з чотирма вершинами,–кількість неорієнтованих простих неізоморфних графів з чотирма вершинами без позначок. Нарисувати усі неорієнтовані прості неізоморфні графи з чотирма вершинами без позначок.

Завдання 5. Знайти кількість усіх позначених неорієнтованих дерев з вершинами?Нарисувати 10 таких дерев.

Завдання 6. Знайти кількість простих неорієнтованих неізоморфних дерев з вершинами. Нарисувати такі дерева.

Завдання 7. Знайти кількість кореневих дерев з вершинами. Нарисувати такі дерева.

Завдання 8. Визначити кількість остовів (каркасів, кістяків) графа , який зображений на рис. 5.1. Наведіть зображення п’яти будь-яких остовів.

Рисунок 5.1 – Граф , для якого визначається кількість остовів

Завдання 9. Скільки остовних дерев є у графів Понтрягіна-Куратовського (і)?

Завдання 10. Скільки остовних дерев має граф ? Скільки остовних дерев має граф?

Завдання 11. Використовуючи матричну формулу Кірхгофа (теорему Кірхгофа), визначити число остовних дерев для кожного з графів, зображених на рис. 5.2.

Рисунок 5.2

Завдання 12. Задаються графи на рис 5.3. Вершини графів упорядковані так, як позначені. Знайти остовні дерева графів пошуком в глибину.

Рисунок 5.3

Завдання 13. Для дерева, яке зображене на рис. 5.4, визначити: висоту дерева; рівень вершини ; рівень вершини; рівень вершини; вершину, яка є предком вершини; вершини, які є синами вершини; листи дерева. Відповідь дати для: а) якщо коренем вибрана вершина; б) якщо коренем вибрана вершина; в) якщо коренем вибрана вершина; г) якщо коренем вибрана вершина; д) якщо коренем вибрана вершина.

Рисунок 5.4

5.4 Приклади аудиторних і домашніх завдань

Завдання 1. Чому дорівнює кількість позначених неорієнтованих простих графів з вершинами іребрами? Нарисувати усі ці графи.

Розв’язок. Кількість позначених неорієнтованих простих графів звершинами іребрами дорівнює числу сполучень з множини різних неорієнтованих пар вершинза числом ребер. Оскільки число вказаних пар вершин дорівнює числу сполучень, то, де.

Тому . Ці три графа представлено на рис. 5.5.

Рисунок 5.5 – Позначені неорієнтовані прості графи з вершинами іребрами

Завдання 2. Чому дорівнює кількість усіх позначених неорієнтованих простих графів з вершинами? Нарисувати усі ці графи.

Розв’язок. Кількість позначених неорієнтованих простих графів звершинами іребрами дорівнює, де. Сумуючи числаза всіма можливими кількостями ребервід випадку безреберного графа до випадку повного графа звершинами, одержуємо числовсіх позначених графів звершинами. Якщо, тоі. Усі позначені неорієнтовані прості графи звершинами наведено на рис. 5.6.

Рисунок 5.6 – Позначені неорієнтовані прості графи з вершинами

Завдання 3. Знайти на рис. 5.6, де представлені неорієнтовані прості графи з вершинами, попарно неізоморфні графи без позначок, нарисувати їх, підрахувати кількістьтаких графів.

Розв’язок. Число попарно неізоморфних графів без позначок з вершинами дорівнює=4. Ці графи наведено на рис. 5.7.

Рисунок 5.7 – Неізоморфні неорієнтовані прості графи з вершинами

Завдання 4. Чому дорівнює кількість усіх позначених неорієнтованих дерев з вершинами? Нарисувати усі ці дерева.

Розв’язок. За формулою Келі число позначених дерев з вершинами дорівнює, тому кількість усіх позначених неорієнтованих дерев звершинами буде.

Усі ці позначені дерева наведено на рис. 5.8.

Рисунок 5.8 – Позначені неорієнтовані дерева з вершинами

Завдання 5. На рис. 5.6, де представлені неорієнтовані прості графи з вершинами, знайти неізоморфні дерева без позначок, нарисувати їх, підрахувати кількістьтаких дерев.

Розв’язок. Число звичайних (неізоморфних) дерев дорівнює 1. Це дерево наведено на рис. 5.9.

Рисунок 5.9 – Дерево з вершинами

Завдання 6. Чому дорівнює кількість кореневих дерев звершинами? Нарисувати усі ці дерева.

Розв’язок.

Усі кореневі дерева з числом вершин представлені на рис. 5.10.

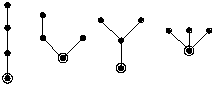
Рисунок 5.10 – Кореневі дерева з вершинами

Завдання 7. Нехай – зв’язний граф з позначеними вершинами. Знайти кількість остовних дерев графа , який зображено на рис. 5.11.

Рисунок 5.11 – Граф

Розв’язок. Для розв’язання завдання використаємо теорему Кірхгофа (матричну формулу Кірхгофа), тобто число остовних дерев у простому зв’язному графі звершинами () дорівнює алгебраїчному доповненню будь-якого елемента матриці Кірхгофа.

Матриця Кірхгофа складається з таких елементів

Запишемо матрицю Кірхгофа для графа

.

Розрахуємо алгебраїчне доповнення елемента матриці

.

Існує вісім остовних дерев графа .

Завдання 8. Побудувати остовне дерево у графі , який зображено на рис. 5.12, використовуючи алгоритм пошуку в глибину.

Рисунок 5.12 – Граф

Розв’язок. Для розв’язання завдання використаємо такий алгоритм пошуку остовного дерева в глибину.

Крок 1. Позначити кожну вершину графа символом.

Крок 2. вибрати довільний елемент графата назвати його коренем дерева.

Крок 3. Замінити позначку вершини з «нов» на «вик» і назначити.

Крок 4. Поки є вершини, які ще не вибрані, суміжні з , виконати такі дії:

а) вибрати вершину , суміжну з;

б) якщо має позначку «нов», додати () в множину(множину ребер остовного дерева, яке будується), замінити позначкуна «вик», назначитиі повторити шаг 4;

в) якщо має позначку «вик» і не є «батьком», додати () в множину(множину зворотних ребер) і повторити шаг 4.

Крок 5. Якщо , назначитиі повторити шаг 4. поки для вершиниє суміжна невикористована вершина, продовжується шлях віддо. Тільки в тому випадку, коли рухатися далі не можна, переходимо до шагу 5, повертаємось до «батька» вершини.

Використаємо цей алгоритм для пошуку остовного дерева графа , що надається на рис. 5.12.

Як корінь довільним способом виберемо вершину . Змінюємо позначкуз «нов» на «вик». Оскільки вершинасуміжна зі має позначку «нов», додаємо ребров множинуі замінюємо позначку вершинина «вик», як наведено на рис. 5.13 а).

Рисунок 5.13

Від вершини переходимо до вершини, оскільки вона є суміжною з. Вершинамає позначку «нов», тому додаємо ребров множинуі заміняємо позначку вершинина «вик», як наведено на рис. 5.13 б).

Тепер вибираємо вершину, яка суміжна з вершиною . Можна вибратиабо. Вибір визначає форму дерева, тому пошук в глибину не продукує дерево єдиним способом. Припустимо, що наступною вершиною буде вершина. Вершинамає позначку «нов», тому додаємо ребров множинуі замінюємо позначку вершинина «вик», як наведено на рис. 5.13 в). З вершинивибираємо вершину, тому що вона є суміжною з. Вершинамає позначку «нов», тому додаємо ребров множинуі заміняємо позначку вершинина «вик», як наведено на рис. 5.13 г). З вершинивибираємо вершину, тому що вона є суміжною з вершиною. Однак вершинавже має позначку «вик», тому додаємо ребров множину, як наведено на рис. 5.14 а).

Рисунок 5.14

Оскільки більше немає ребер для перевірки на суміжність з вершиною , окрім «батька», вертаємось до вершини(далі не будемо згадувати «батька» як можливу суміжну вершину). Інших ребер для перевірки на суміжність з вершиноютеж немає, тому вертаємось до. Тут є єдиною вершиною для перевірки є вершина, але вершинавже має позначку «вик», тому ребрододаємо ві вертаємось в вершину, як наведено на рис. 5.14 б).

Ребер для перевірки на суміжність з вершиною більш немає, тому повертаємось до вершини. Помітимо, що якби була можливість досягти кожну вершину, побудувавши шлях з, то поки дерево не побудовано повністю, не треба було б повертатися у вершину. Повернувшись у вершину, можна вибратиабо. Припустимо, що вибрали вершину. Так як вершинамає позначку «нов», тому додаємо ребров множинуі заміняємо позначку вершинина «вик», як наведено на рис. 5.14 в).

Вершина суміжна з вершиноюі має позначку «нов». Додаємо ребров множинуі замінюємо позначку вершинина «вик», як наведено на рис. 5.15 а).

Припустимо тепер, що вибрана вершина , тому що вона є суміжною з вершиною. Але вершинавже має позначку «вик», тому ребрододаємо ві вертаємось в вершину, як наведено на рис. 5.15 б).

Оскільки вершина суміжна з, додаємо ребров множинуі замінюємо позначку вершинина «вик», як наведено на рис. 5.15 в).

Більш немає вершин для перевірки з вершини , тому повертаємось у вершину. Але більш немає вершин для перевірки з вершини, тому повертаємось у вершину. Оскільки немає більш вершин для перевірки з вершини, повертаємось у вершину. Інших вершин для перевірки з вершинитеж немає, тому процес завершується.

Рисунок 5.15

Остовним деревом графа є дерево, яке наведено на рис. 5.16.

Рисунок 5.16

Завдання 9. Нехай існує орієнтоване упорядковане дерево (рис. 5.17). Для цього дерева визначити: висоту дерева; глибину, висоту, рівень вершини 8; листя, їх рівні, глибину, висоту.

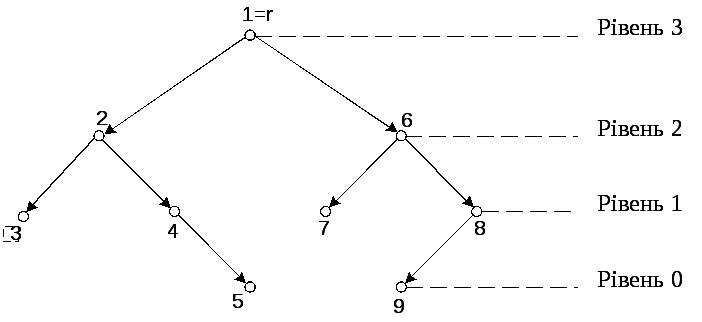
Рисунок 5.17 – Кореневе дерево, упорядковане за рівнями

Розв’язок. Дерево упорядковане, множина синів кожної вершини упорядкована зліва направо:. Висота дерева, яке зображене на рис. 5.17, тобто число дуг найдовшого шляху (висота кореня) дорівнює 3. Вершина 8 має глибину 2, тобто довжина шляху з кореневої вершиниу вершину 8 дорівнює 2. Вершина 8 має висоту 1, тобто довжина найдовшого шляху з вершини 8 до будь-якого листа (до листа 9) дорівнює 1. Рівень вершини 8, тобто різниця між висотою всього дерева і глибиною цієї вершини, дорівнює 1.

Листям дерева є вершини 3, 5, 7, 9. Їх рівні та глибина такі: листя 3,7 мають рівень 1, глибину 2; листя 5, 9 мають рівень 0, глибину 3. Висота будь-якого листа дорівнює 0.