18.3.Скорость и ускорение гармонических колебаний

Если материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат тогда зависимость координаты х от времени t описывается уравнением (19.1). Скорость и ускорение a колеблющееся точки соответственно равны:

, (19.17)

и , (19.18)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды скорости и ускорения колебаний соответственно равны υ_max = А и a_max= А₀². Фаза скорости (19.17) отличается от фазы величины (19.1) на , а фаза ускорения (19.18) отличается от фазы величины (19.1) на. В момент времени, когдах=0 скорость колеблющейся точки максимальна по величине и равна амплитуде скорости в моменты прохождения колеблющейся точки через положение равновесия. При максимальных смещениях (х =±А) скорость равна нулю. Вектор скорости всегда направлен в сторону движения.

Ускорение равно нулю при прохождении колеблющейся точки через положение равновесия и достигает максимального по величине значения, которое равно амплитуде ускорения, при максимальных смещениях колеблющейся точки. Вектор ускорения всегда направлен в сторону положения равновесия. Удаляясь от положения равновесия, колеблющаяся точка движется, замедлено, приближаясь к нему – ускоренно.

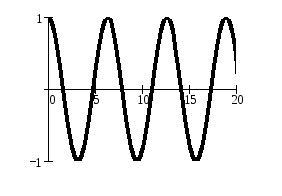
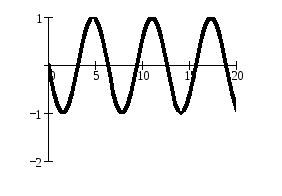
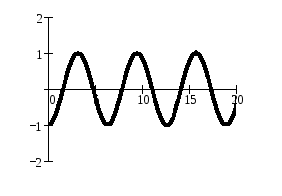
Рис.19.4.

График гармонического колебания, который описывается уравнением (19.1), скорость гармонического колебания, описываемая уравнением (19.17), и ускорение (19.18) показаны на рис.19.4. Видно, что смещение, скорость и ускорение гармонически колеблющейся точки являются периодическими функциями от времени с одинаковыми периодами.

19.4. Энергия колебаний Кинетическая энергия материальной точки, совершающей гармонические колебания равна

(19.19)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F равна

(19.20)

Подставляя значения, получаем выражение для потенциальной энергии колеблющегося тела.

Полная энергия, по закону сохранения энергии, остается постоянной. Сложив (19.19) и (19.20) получим формулу для полной энергии:

(19.21)

Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.

Из (19.21), видно, что значение полной энергии зависит прямо пропорционально от массы колеблющегося тела, а также от квадрата амплитуды.

Применяя, строительные машины и механизмы колебательными движениями разрушаются старые дома или дизель молотом вбиваются сваи в грунт.

19.5.Сложение гармонических колебаний

вдоль одного направления с одинаковой частотой

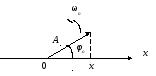
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, другими словами колебания необходимо сложить. Решение сложения нескольких колебаний одинакового направления, значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой. Для сложения колебаний одного направления и одинаковой частоты воспользуемся методом вращающегося вектора амплитуды А. Возьмем ось, которую обозначим буквой х. Из точки О, взятой на оси х, отложим вектор длины А, образующий с осью угол φ_о, как показано на рис. 19.5(а). Если привести этот вектор во вращение с угловой скоростью ω₀. то проекция конца вектора будет перемещаться по оси х в пределах от -А до +А, причем координата этой проекции будет изменяться со временем по закону, описанному уравнением (19.1). Следовательно, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой φ₀. Угол φ₀, который образуется между вектором амплитуды с осью х в начальный момент времени, рис.19.5(а).

Если необходимо сложить два гармонических колебания с одинаковыми частотами с помощью векторных диаграмм легко осуществить сложение гармонических колебаний.

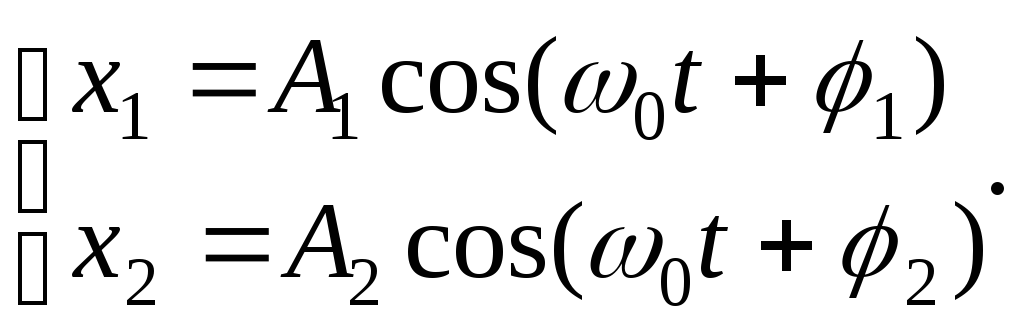(19.22)

Представим оба колебания с помощью векторов амплитуд А₁ и А₂, и начальных фаз φ₁ и φ₂ складываемых колебаний. Построим векторные диаграммы этих колебаний, как показано на рис. 19.5(б).

а	б
Рис.19.5.

Так как векторы А₁ и А₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂- φ₁) между ними остается постоянной. Легко видеть, что проекция этого вектора на ось х равна сумме проекций слагаемых векторов:

. (19.23)

Следовательно, вектор А представляет собой амплитуду результирующего колебания; φ - начальная фаза.

Амплитуда результирующего колебания определяется как:

. (19.24)

Фаза колебаний φ определяется как тангенс угла наклона результирующей амплитуды.

. (19.25)

Тело участвует в двух гармонических колебаниях одного направления и одинаковой частоты совершает также гармонические колебания в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ₁- φ₂) складываемых колебаний.