4.6. Кинетическая энергия вращения

Рассмотрим абсолютно твердое тело, вращающееся около неподвиж­ной осиz, проходящей через него (рис.4.8). Мысленно разобьем это тело на маленькие объемы с элементарными мас­сами m₁, m₂, ..., т_n, находящиеся на рас­стоянии r₁, r₂ , ..., r_n от оси вращения. При вращении твердого тела относительно не­подвижной оси отдельные его элементар­ные объемы массами m_i опишут окружно­сти различных радиусов r_i, и имеют раз­личные линейные скорости _i. Но так как мы рассматриваем абсолютно твердое те­ло, то угловая скорость вращения этих объемов одинакова:

ω = υ₁/ r₁ = υ₂/ r₂ = … = υ_n/ r_n . (4.8)

Кинетическую энергию W_вр вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

или

.

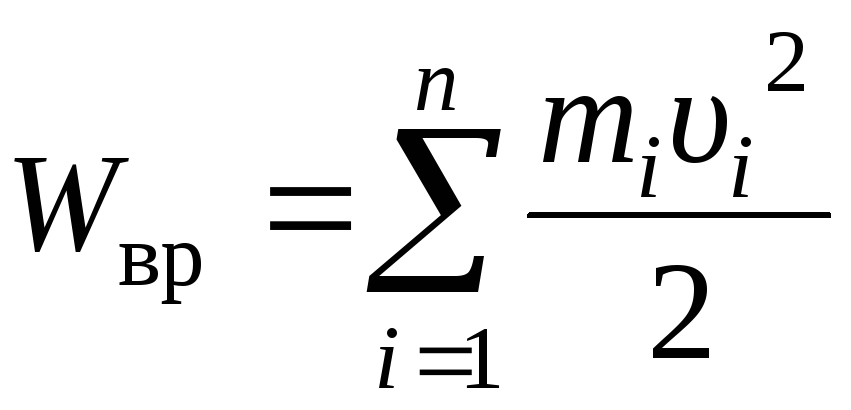Используя выражение (4.5), получим

,

где I_z - момент инерции тела относитель­но оси z. Таким образом, кинетическая энергия вращающегося тела

W_вр = I_zω²/2. (4.9)

Из сравнения формулы (4.6) с вы­ражением для кинетической энер­гии тела, движущегося поступательно (W_к = mυ²/2), следует, что момент инерции вращательного движения - мера инер­тности тела. Формула (4.9) справедлива для тела, вращающегося вокруг непод­вижной оси.

В случае плоского движения тела, на­пример цилиндра, скатывающегося с на­клонной плоскости без скольжения, энер­гия движения складывается из энергии поступательного движения и энергии вра­щения:

W = mυ_c²/2 + I_cω²/2, (4.10)

где m - масса катящегося тела; υ_c - ско­рость центра масс тела; I_c - момент инерции тела относительно оси, проходя­щей через его центр масс; ω - угловая скорость тела.

4.7. Уравнение динамики вращательного движения твердого тела

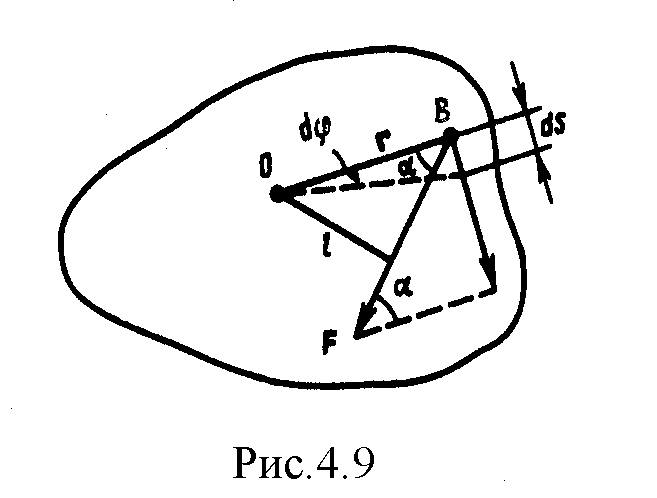Найдем выражение для работы при вращении тела (рис.4.9). Пусть сила приложена в точкеВ, находящейся от оси вращения на расстоянии ά - угол между направлением силы и радиусом-вектором . Так как тело абсолютно твер­дое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый уголdφ точка приложения В проходит путь ds = rdφ, и работа равна произведению проекции силы на направление смещения на величину смещения:

δA = F sinά rdφ .

Учитывая (4.1), можем записать δA = M_z dφ,

где Fr sinά = Fl = M_z - момент силы от­носительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол пово­рота.

Работа при вращении тела идет на увеличение его кинетической энергии:

δA = dW_к ,

но

dW_к = d(I_z ω²/2) = I_z ω dω

поэтому

M_z dφ = I_z ω dω

или

.

Учитывая, что , получим

. (4.11)

Уравнение (4.11) представляет собой уравнение динамики вращательного дви­жения твердого тела относительно непод­вижной оси.

Можно показать, что если ось враще­ния совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

, (4.12)

где I - главный момент инерции тела (момент инерции относительно главной оси).