ЛЕКЦИИ спецглавы высшей математики / ЛЕКЦИЯ_5 / Паршин_Лекция19_Эйконал

ЛЕКЦИЯ 19

Геометрическая оптика, уравнение эйконала. Принцип Ферма. Дуализм описания электромагнитных явлений при ¸ ! 0. Фотон и вероятность его обнаружения.

Геометрическая оптика, уравнение эйконала

Плоская монохроматическая электромагнитная волна отличается тем свойством, что направление ее распространения, характеризуемое волновым вектором k, и амплитуда E0 везде одинаковы

Произвольные электромагнитные волны этим свойством, конечно, не обладают. Однако, часто электромагнитные волны, не являющиеся плоскими, тем не менее таковы, что их можно рассматривать как плоские в каждом небольшом участке пространства. Для этого необходимо, чтобы амплитуда и направление волны почти не менялись на протяжении расстояний порядка длины волны ¸.

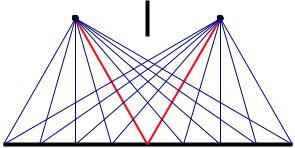
л"чи

л"чи

%олно%ы) *о%)+,но-.и

%олно%ы) *о%)+,но-.и

Рис. 1: Лучи и волновые поверхности.

Если выполнено это условие, то можно ввести, так называемые, волновые поверхности во всех точках которых фаза волны в данный момент времени одинакова (для плоской волны это плоскости, перпендикулярные к направлению ее волнового вектора k). В каждом небольшом участке пространства можно говорить о направлении распространения волны, нормальном к волновой поверхности. При этом можно ввести понятие лучей линий, касательная к которым в каждой точке совпадает с направлением распространения волны рис. 1.

1

Изучение законов распространения волн в этом случае составляет предмет геометрической оптики. Геометрическая оптика рассматривает, следовательно, распространение электромагнитных волн, в частности света, как распространение лучей, совершенно отвлекаясь при этом от их волновой природы. Другими словами, геометрическая оптика соответствует предельному случаю малых длин волн, ¸ ! 0.

Выведем теперь основное уравнение геометрической оптики уравнение, определяющее направление лучей. Пусть f есть любая из величин, описывающих поле волны (E или H). В плоской монохроматической волне f имеет вид

В случае, когда волна не плоская, но геометрическая оптика применима, амплитуда a является, вообще говоря, функцией координат и времени, а фаза Ã, называемая также эйконалом, не имеет такого простого вида как kr ¡ !t + ®. Очень важно, однако, что эйконал является большой величиной. Это видно уже из того, что он меняется на 2¼ на масштабах длины волны, а геометрическая оптика соответствует пределу ¸ ! 0 (т. е. все расстояния считаются много больше ¸).

В малых участках пространства и интервалах времени эйконал Ã мож-

Начало координат выбрано в рассматриваемом участке пространства и интервала времени. Сравнивая это с выражением для плоской волны

Однако, с другой стороны, для плоской волны имеет место соотношение

2

Это есть уравнение эйконала одно из основных уравнений геометрической оптики.

Если волна обладает определенной постоянной частотой !, то зависимость поля волны от времени определяется множителем e¡i!t. Поэтому, для эйконала такой волны мы можем написать

где Ã0 функция только от координат. В этом частном случае уравнение эйконала принимает вид

Волновые поверхности являются поверхностями постоянного эйконала, т. е. семейством поверхностей вида

Лучи в каждой точке нормальны к соответствующей волновой поверхности; их направление определяется градиентом rÃ0.

Принцип Ферма

Рассмотрим световой луч, распространяющийся из одной точки пространства A в другую точку B по траектории, изображенной на рис. 2. Величину Ã0 в точке A примем за начало отсчета: Ã0(A) = 0 и найдем

B

A

Рис. 2: Траектория луча света.

чему равна величина Ã0(B). Для этого разобьем луч (траекторию) на множество маленьких отрезков, так что в пределах каждого из них луч представлялся бы отрезком прямой, тогда фаза, набираемая на каждом таком участке, будет равна

3

где ki волновой вектор света, соответствующий данному участку. Величина Ã0(B) определяется тогда интегралом

Пусть все возможные пути непрерывным образом заполняют все пространство. Спрашивается тогда, какие из путей дают наибольший вклад в сумму. Такой вопрос правомочен, поскольку при ¸ ! 0 величины Ã0S(B) велики и меняются на величину много больше 2¼ при переходе от одного пути к другому даже, если эти пути очень близки в пространстве. Поэтому, слагаемые в сумме (14) очень быстро осциллируют и почти все уничтожают (взаимно сокращают) друг друга.

S 1

B

A

Рис. 3: Разные пути, соединяющие точки A и B.

Исключение составляют лишь те пути (и близкие к ним), для которых различие в фазах Ã0(B) составляет величину второго порядка малости по отношению к отличию путей друг от друга. В результате

A

4

Пути близкие к тому, который обеспечивает экстремальное значение интеграла, вносят в сумму примерно одинаковый вклад. Поэтому, часто говорят, что лучи света распространяются по траектории для которой значение интеграла R kdl экстремально (минимально или максимально). Этот принцип называется принципом Ферма.

В вакууме k = (!=c)n, где n единичный вектор вдоль направления луча (ndl = dl). Так, что принцип Ферма сводится к условию

A

Но R dl это длина пути, соединяющего точки A и B. Таким образом, эта длина должна быть минимальной, что соответствует прямолинейному распространению лучей в вакууме. Иногда принцип Ферма формулируют следующим образом: свет распространяется таким образом, чтобы время его распространения было минимальным. На самом деле это, как мы видим, необязательно. Требуется лишь условие экстремальности.

Рассмотрим несколько примеров.

1. Отражения от плоского зеркала.

S P

A B C D E F K L M

Рис. 4: Отражение света от плоского зеркала.

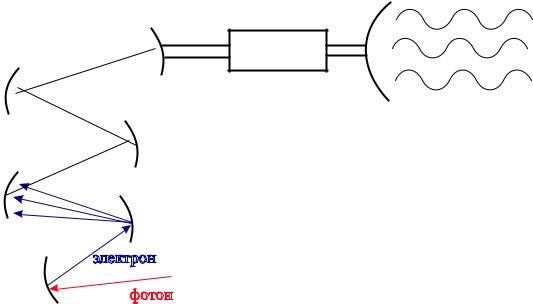
Имеется источник и приемник (S и P ) и преграда Q, чтобы свет прямо не попадал из источника в приемник рис. 4. Вклад от траекторий (более длинных) SAP , SBP и т. д. взаимно уничтожает друг друга в результате интерференции. Основной вклад в точке P дает траектория SEP как соответствующая минимуму R kdl = k R dl = klрис. 5.

Вклад от траекторий SAP , SBP и т. д. можно сделать заметным, если процарапать зеркало в тех местах, которые дают противополож-

5

t

x

E

Рис. 5: Время распространения света как функция координаты x.

ный по знаку вклад. Например, если вклад SBP сокращает вклад SAP , то исключим точку B и ее окрестность из рассмотрения, процарапав зеркало в соответствующем месте. Если мы правильно нанесем царапины, убрав из суммы все отрицательные слагаемые, то мы существенно увеличим интенсивность в точке P . Такое ¾исцарапанное¿ зеркало называется дифракционной решеткой.

2.Отражение от эллиптического зеркала.

Ликвидировать взаимное сокращение вкладов при отражении от различных точек зеркала можно и другим путем взять и прогнуть зеркало придав ему форму эллипса рис. 6, так, чтобы S и P были

S P

A I

B C D E F G H

Рис. 6: Эллиптическое зеркало.

фокусами этого эллипса. Тогда, как известно, пути SAP = SBP = SCP и т. д., т. е. все пути вносят одинаковый (или почти одинаковый) вклад. От этого освещение в точке P возрастает на много порядков.

3.Фокусирующая линза.

Основной вклад в отсутствии линзы дает траектория SMP . Она соответствует минимальному времени распространения света из S в

6

A

M

S P

Рис. 7: Как сделать, чтобы время прохождения света по траектории SAP равнялось бы времени прохождения света по траектории SMP ?

P по прямой. Вклад остальных путей взаимно уничтожается. Однако, свет можно перехитрить. Сделаем так, чтобы его движение по всем траекториям занимало одинаковое время. Мы знаем, что свет распространяется в стекле медленнее, чем в воздухе. Поэтому, поместим стекло нужной толщины на кратчайшем пути, проходящем через точку M. Толщину подберем из условия, чтобы теперь время путешествия света из S в P (через M) было бы равно времени его прохождения по траектории SAP . Для соседних с M траекторий сделаем тоже самое. Но, поскольку эти траектории длиннее, там не понадобится такое толстое стекло, как в точке M. В результате получаем рис. 8. Такое стекло, как известно, называется фокуси-

A

M

S P

Рис. 8: Фокусирующая линза.

рующей линзой! Из этих примеров ясно, что свет на самом деле распространяется сразу по всем путям. Просто действие большинства из них сокращается в обычной ситуации.

7

F

Рис. 9: Отражение света от сферического зеркала.

Этот пример демонстрирует, что свет не всегда выбирает самый короткий путь. Иногда приходится выбирать самый длинный. Для этого рассмотрим отражение света от сферического зеркала рис. 9. Точки S и P расположены на концах диаметра зеркала. Опять есть множество путей. Из всех них путь SF P максимальный и поэтому свет выбирает его. Число примеров такого рода можно бесчисленным числом способов размножить рис. 10.

Дуализм описания электромагнитных явлений при ¸ ! 0. Фотон и вероятность его обнаружения

Из вышесказанного следует, что при ¸ ! 0 многие оптические явления можно описывать двумя способами. Чисто классически, используя понятие о частицах, фотонах, которые движутся по законам геометрической оптики или с помощью представления о волнах, интерференция которых так хорошо наблюдаема на эксперименте с двумя щелями и которую довольно затруднительно объяснить, используя представление о

8

частицах.

Наоборот, ряд явлений, происходящих со светом, трудно объяснить, используя представление о волнах. К числу последних относится фотоэффект, о котором более подробно мы поговорим на следующей лекции. Его можно понять, если использовать представление о свете как о частицах, обладающих энергией ~! и импульсом ~k. Таким образом, налицо, так называемый корпускулярно волновой дуализм.

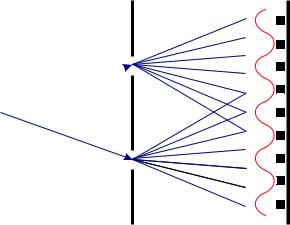
Так что же такое свет: частицы или волны? Правильный ответ заключается в том, что свет существует именно в виде частиц фотонов!. Как же можно обнаружить отдельный фотон? Один из используемых для этого приборов называется фотоумножителем рис. 11.

L

+ +

.инамик

+

B

эл'к#)он

A

!о#он

Рис. 11: Фотоумножитель.

Когда фотон ударяется о металлическую пластинку A, он выбивает электрон из одного из атомов пластинки. Свободный электрон притягивается к пластинке B (заряженной положительно) и, ударившись о нее выбивает 3 или 4 электрона. Каждый из электронов, выбитых из пластинки B, притягивается к пластинке C (которая тоже заряжена положительно) и, столкнувшись с пластинкой, высвобождает еще больше электронов. Этот процесс повторяется десять, двенадцать раз, пока миллиарды электронов, способные создать ощутимый электрический ток, не ударятся в последнюю пластинку L. Этот ток можно усилить обычным усилителем и пропустить через динамик, чтобы были слышны щелчки. Каждый раз, когда фотон данного цвета попадает в фотоумножитель, раздается щелчок одной и той же громкости.

9

Если на фотоумножитель падает достаточно сильный световой поток, в котором много фотонов, то фотоумножитель трещит не переставая и мы даже не различаем отдельных щелчков. Однако, по мере ослабления интенсивности щелчки станут более редкими, так что их можно пересчитывать. Важно при этом, что они сохраняют свою громкость. Если свет это частицы, то как же тогда объяснить явления интерференции и дифракции, свойственные, казалось бы, только волнам. Рассмотрим эксперимент с двумя щелями рис. 12.

Рис. 12: Эксперимент с двумя щелями.

На экране за щелями расположим фотоумножители в точках, соответствующих минимумам и максимумам классической интерференционной картины. Источник S возьмем очень слабый, так чтобы различить по времени отдельные щелчки фотоумножителей. Пусть, например, в среднем эти щелчки раздаются раз в минуту. Мы тогда довольно легко обнаружим, что щелкают только те фотоумножители, которые расположены в точках соответствующих максимумам интерференционной картины. А в точках минимума никаких щелчков раздаваться не будет. Второе, что мы заметим, что нет никакой закономерности в последовательности щелчков. После щелчка в первом фотоумножителе может щелкнуть 9-й, а затем 5-й и т. д., так что никакой закономерности мы не заметим. Однако, после достаточно большого числа щелчков (например, 10000) мы увидим, что (в среднем) каждый нечетный фотоумножитель щелкает одинаково часто, хотя число щелчков у каждого и не равно строго друг другу. Однако, с течением времени относительная разница выравнивается. Это в какой-то мере напоминает случайное заполнение нескольких эквивалентных ящиков молекулами, когда молекула с равной вероятностью может оказаться в любом из ящиков. Оказывается, это на самом

10