
- •Министерство Российской Федерации по связи и информатизации
- •Глава 1. Высказывания, формулы, тавтологии.
- •Отношения логической эквивалентности и логического следствия.
- •Задачи.
- •Глава 2. Формальные теории.
- •Глава 3. Исчисление высказываний.
- •Построение вывода в логике высказываний.
- •Задачи.
- •Глава 4. Метод резолюций в логике высказываний.
- •Задачи.
- •Глава 5. Предикаты.
- •Задачи.
- •Глава 6. Исчисление предикатов.
- •Теория равенства.
- •Формальная арифметика.
- •Теория частично упорядоченных множеств.
- •Задачи.
- •Глава 7. Алгоритмы.
- •Глава 8. Рекурсивные функции.
- •Задачи.
- •Глава 9. Машины Тьюринга.
- •Операции с машинами Тьюринга.
- •Принцип двойственности.
- •Способы композиции машин Тьюринга.
- •Задачи.
- •Ответы и указания.
Построение вывода в логике высказываний.
Пример.
Докажем, что
выводима формула
![]() .
Сокращенно это записывается так: ├
.
Сокращенно это записывается так: ├![]() .
.
По теореме, обратной теореме дедукции, посылку можно перенести в левую часть:
![]() ├
├![]() .
.
Проделаем эту операцию еще раз:
![]() ,
,
![]() ├
├![]() .
.
Таким
образом, нам нужно доказать, что из
формул
![]() и
и![]() выводима формула
выводима формула![]() .
Составим вывод формулы
.
Составим вывод формулы![]() .
В каждой строке вывода записывается
только одна формула. В правой части
страницы удобно указывать комментарий,
– что собой эта формула представляет.
Возможны варианты:
.
В каждой строке вывода записывается
только одна формула. В правой части
страницы удобно указывать комментарий,
– что собой эта формула представляет.
Возможны варианты:
гипотеза,
аксиома (может быть, с какими-то подстановками),
ранее доказанная теорема,
формула получена из предыдущих формул по правилу Modus ponens.
Вначале мы запишем гипотезы.
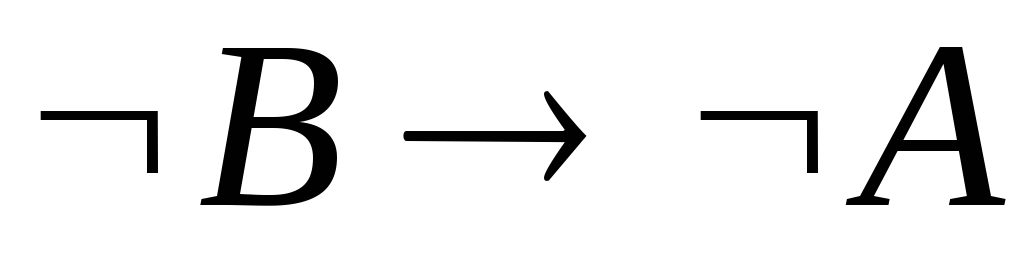 –гипотеза.
–гипотеза. –гипотеза.
–гипотеза.
Формулу
![]() удобно получить из аксиомы А3. Поэтому
запишем эту аксиому:
удобно получить из аксиомы А3. Поэтому
запишем эту аксиому:
3.
![]() А3.
А3.
К формулам 1 и 3 можно применить правило вывода Modus ponens (что мы и отметим в комментарии). Порядок номеров формул существенен (первой указывается посылка).
4.
![]() .
МР
1, 3.
.
МР
1, 3.
Посылку
в формуле 4 можно получить из аксиомы
А1, если заменить
![]() на
на![]() :
:
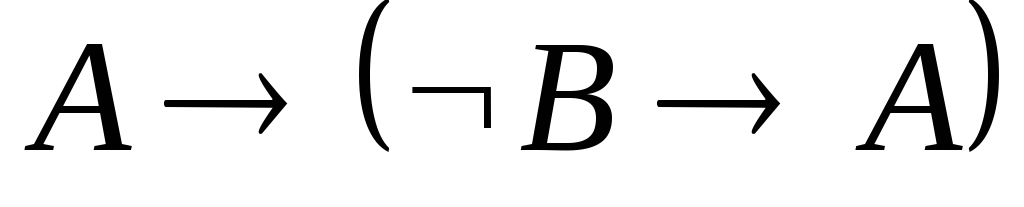 .
А1 с подстановкой вместо
.
А1 с подстановкой вместо
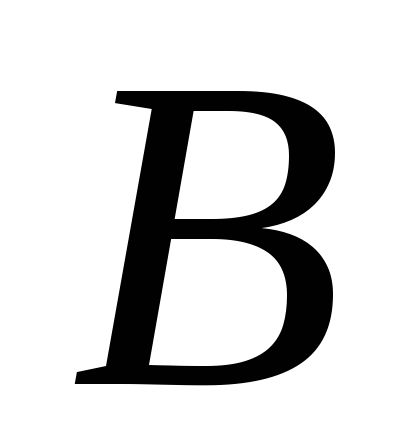 –
– .
.
Далее дважды применяем правило Modus ponens:
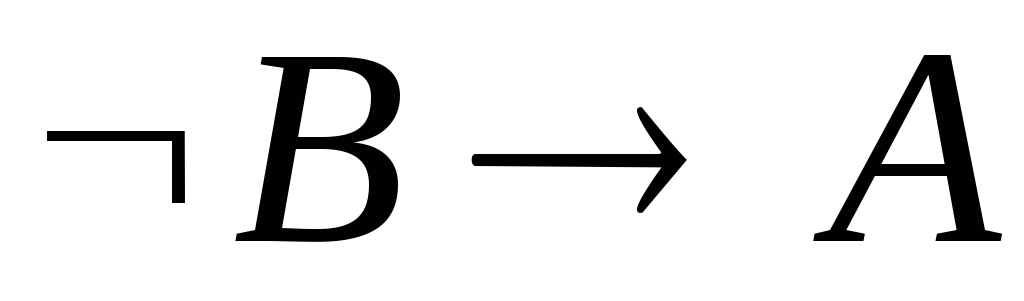 .
МР 2, 5.
.
МР 2, 5.
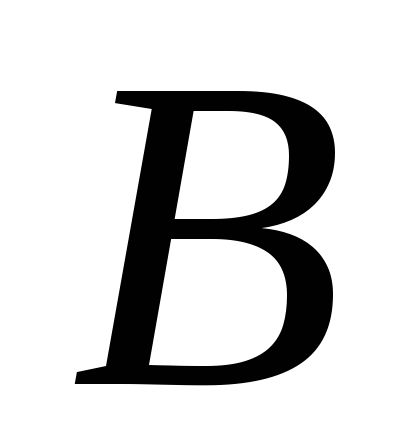 .
МР 6, 4.
.
МР 6, 4.
Вывод построен, и применением теоремы дедукции мы доказали выводимость первоначальной формулы.
Отметим, что вывод может быть неединственным, в частности, формулы могут быть записаны в другом порядке. Решение данной задачи может быть оформлено следующим образом:
├![]() .
.
По теореме, обратной теореме дедукции,
![]() ├
├![]() .
.
![]() ,
,
![]() ├
├![]() .
.
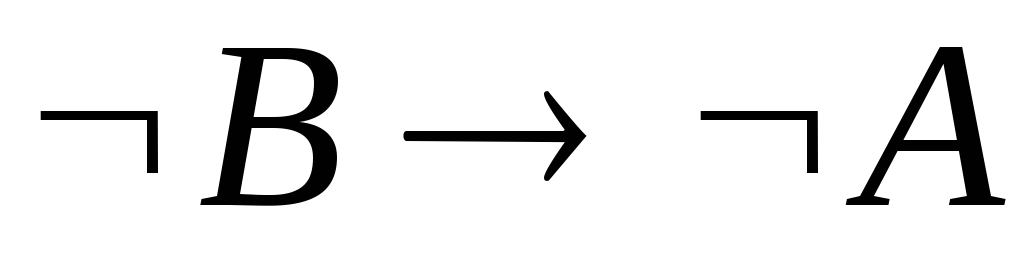 –гипотеза.
–гипотеза. –гипотеза.
–гипотеза.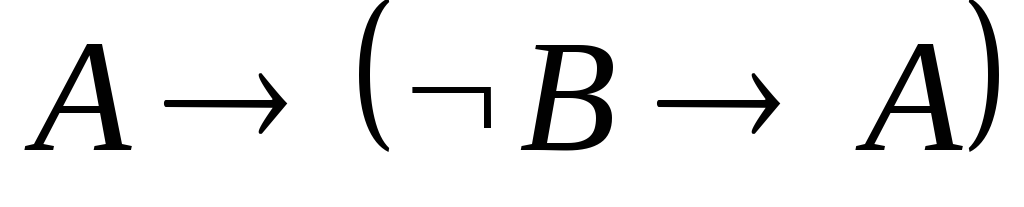 .
А1,
.
А1,
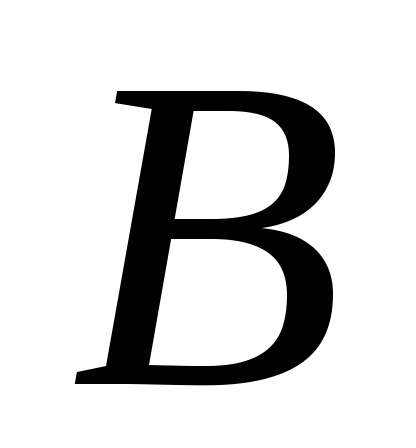 :
: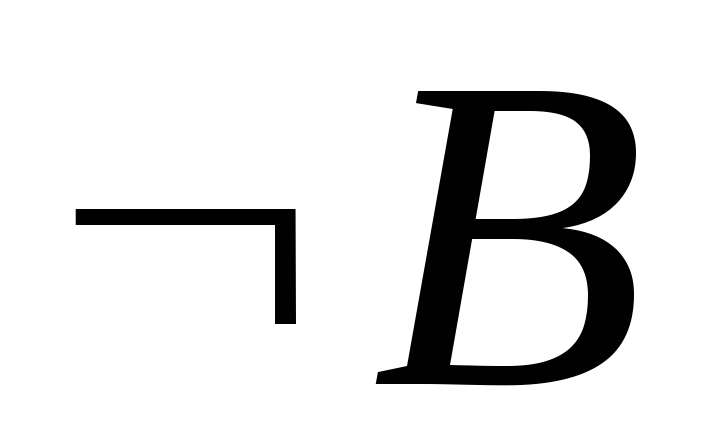 .
.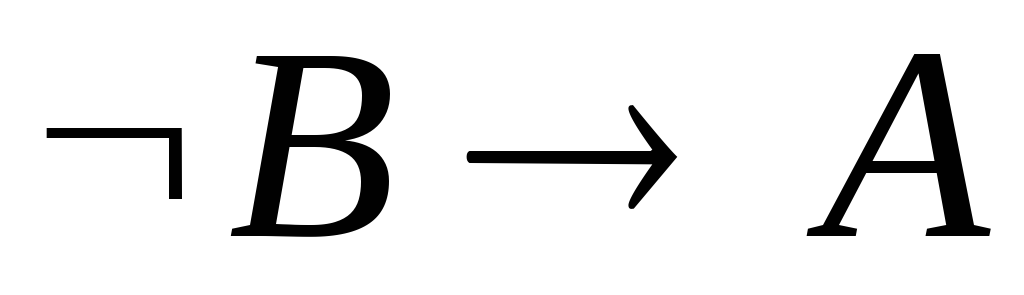 .
МР 2, 3.
.
МР 2, 3.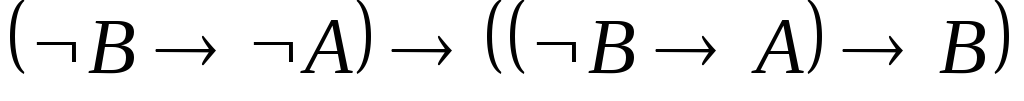 .
А3.
.
А3. .
МР
1, 5.
.
МР
1, 5.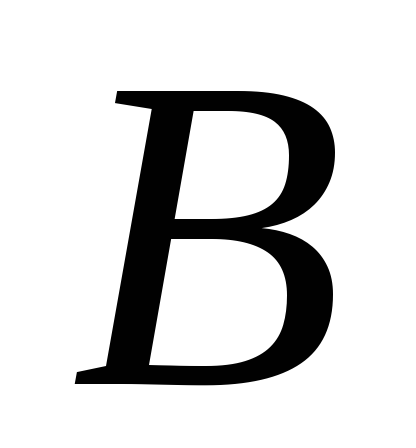 .
МР 4, 6.
.
МР 4, 6.
Пример.
Данный пример
более прост, но достаточно показателен.
Обратите внимание, что здесь не
используются ни аксиомы, ни теоремы.
Доказательство теоремы ├![]() строится только на основании правила
МР.
строится только на основании правила
МР.
По теореме, обратной теореме дедукции,
![]() ├
├![]() .
.
![]() ,
,
![]() ├
├![]() .
.
![]() ,
,
![]() ,
,![]() ├
├![]() .
.
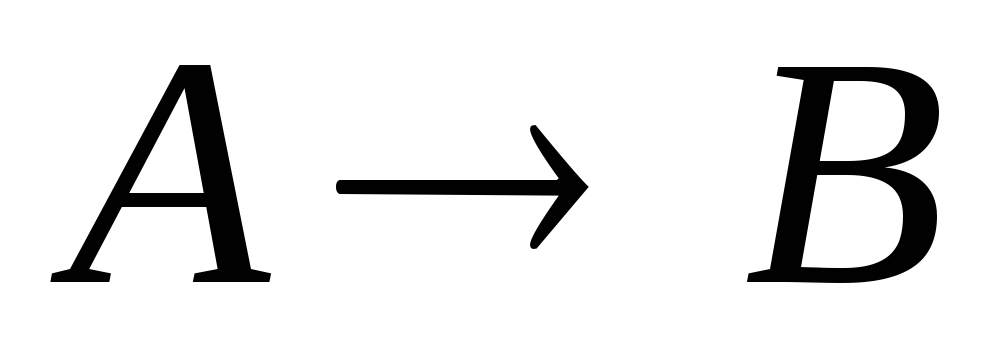 –гипотеза.
–гипотеза.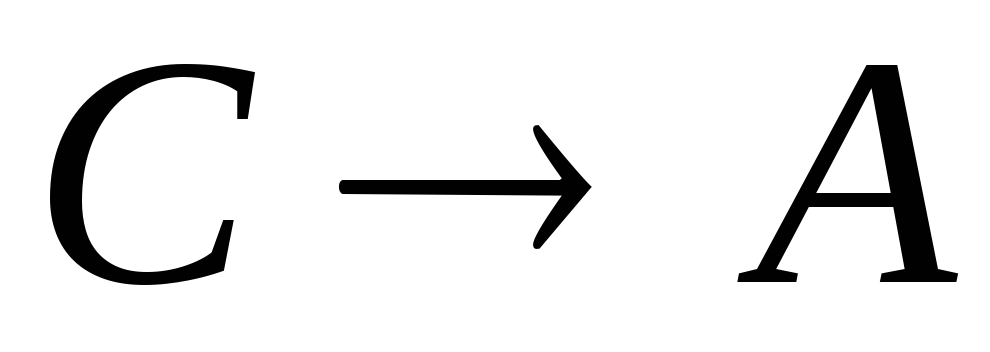 –гипотеза.
–гипотеза. –гипотеза.
–гипотеза. .
MP
3,2.
.
MP
3,2.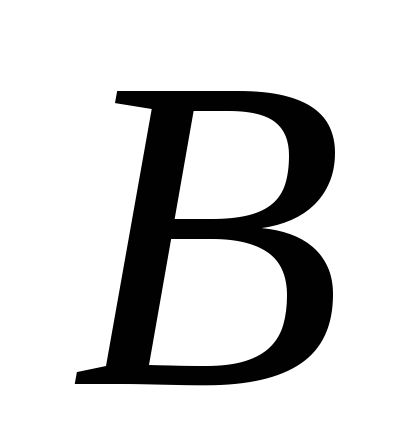 .
MP
4,1.
.
MP
4,1.
В Содержание.
Задачи.
Указать, какие из следующих выражений являются формулами исчисления высказываний.
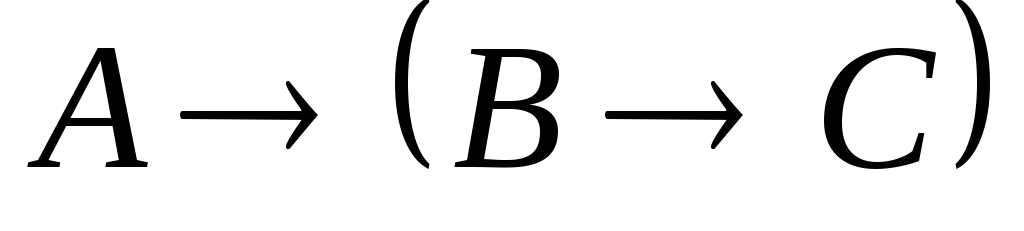 .
.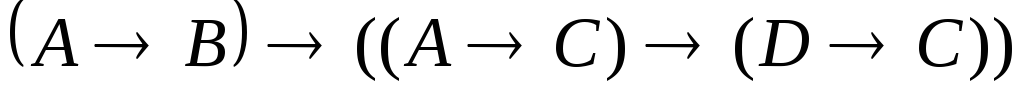 .
. .
.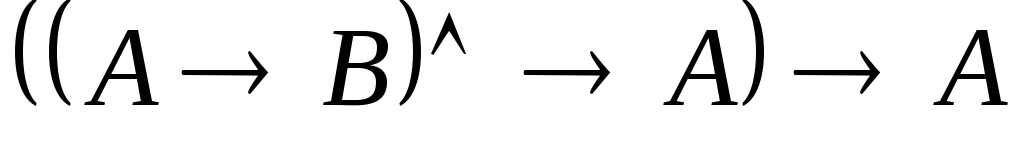 .
.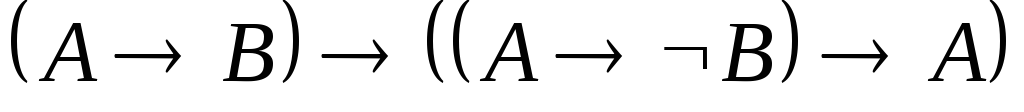 .
.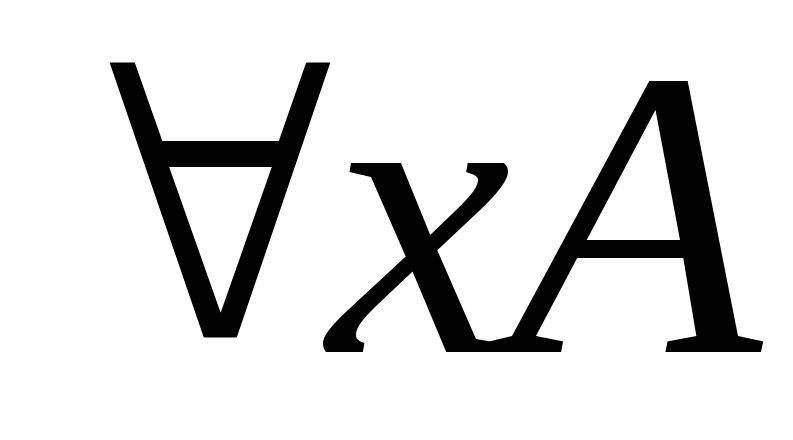 .
.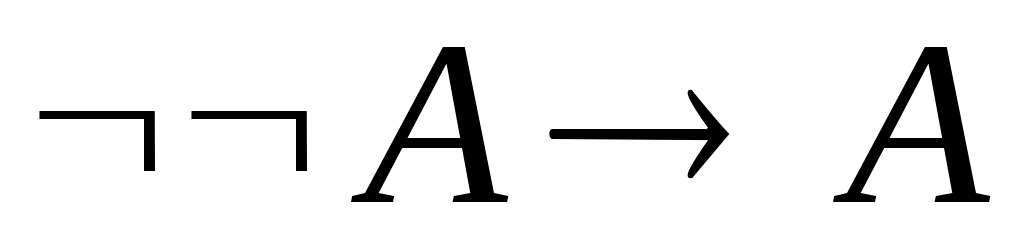 .
.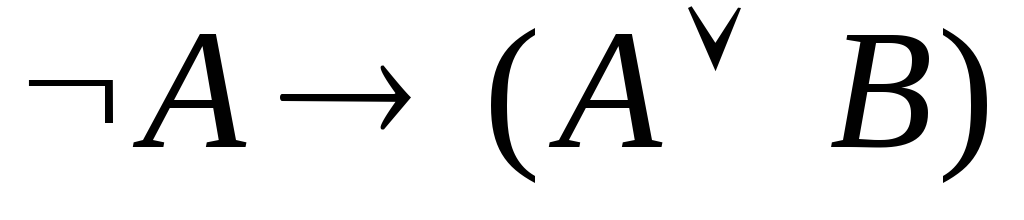 .
. .
.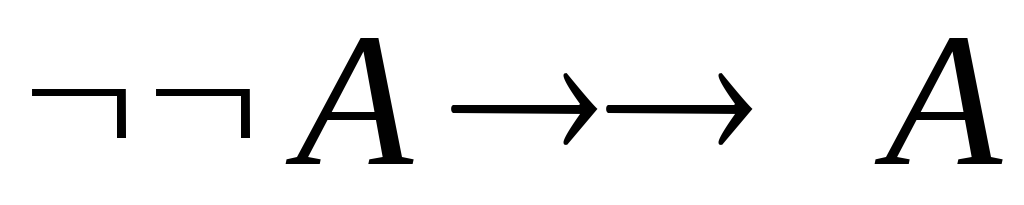 .
.
2. Какая из приведенных
ниже записей является выводом формулы
![]() в исчислении высказываний?
в исчислении высказываний?
По теореме, обратной теореме дедукции, ├
 равносильно
равносильно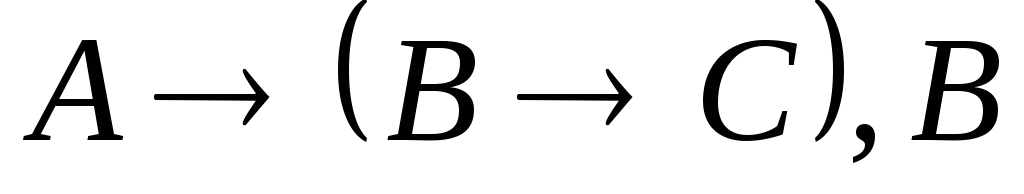 ├
├ .
.
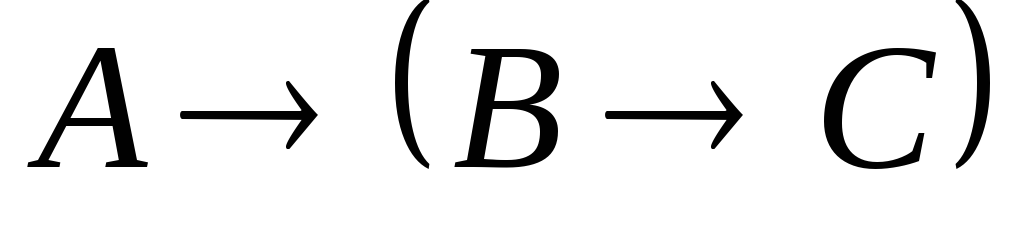 –гипотеза.
–гипотеза.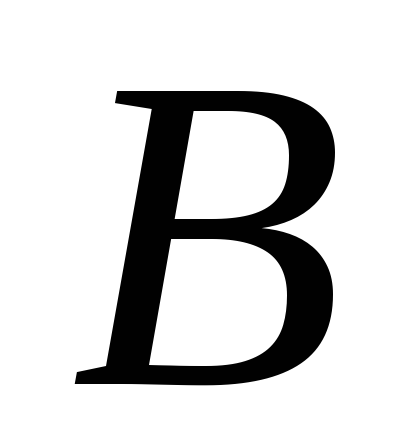 –гипотеза.
–гипотеза. .
MP
2,1.
.
MP
2,1.
По теореме, обратной теореме дедукции, ├
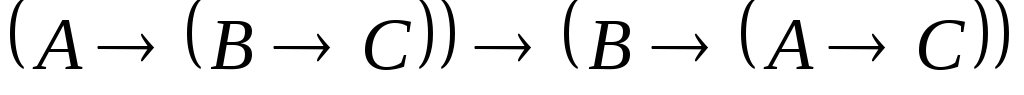 равносильно
равносильно ├
├ .
.
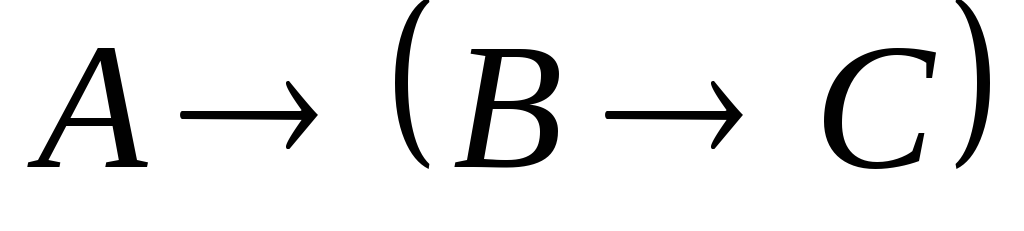 –гипотеза.
–гипотеза.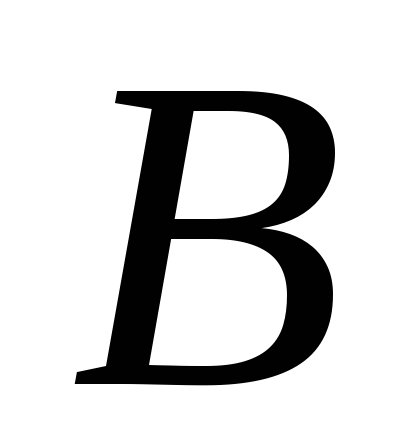 –гипотеза.
–гипотеза. –гипотеза.
–гипотеза.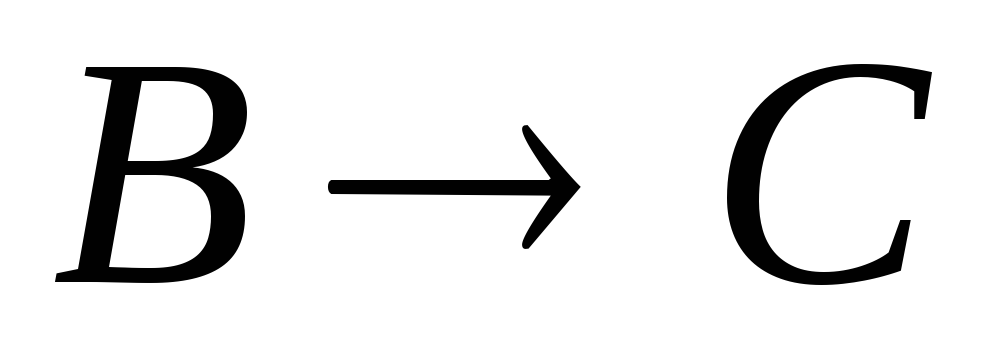 .
MP
3,1.
.
MP
3,1. .
MP 2,4.
.
MP 2,4.
По теореме, обратной теореме дедукции, ├
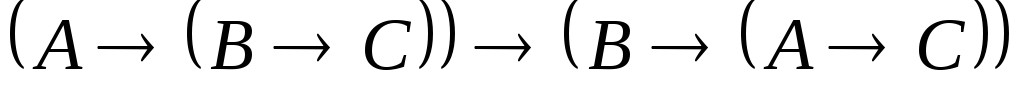 равносильно
равносильно ├
├ .
.
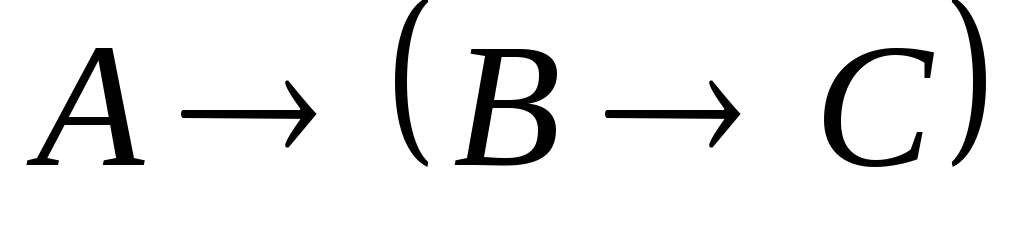 –гипотеза.
–гипотеза.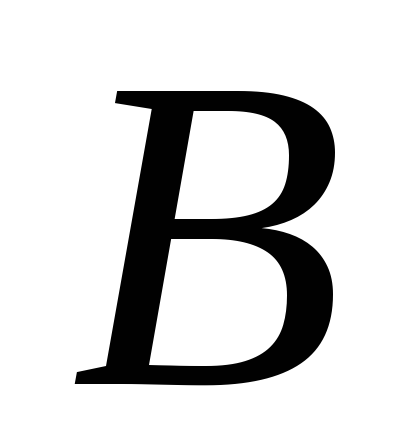 –гипотеза.
–гипотеза. –гипотеза.
–гипотеза.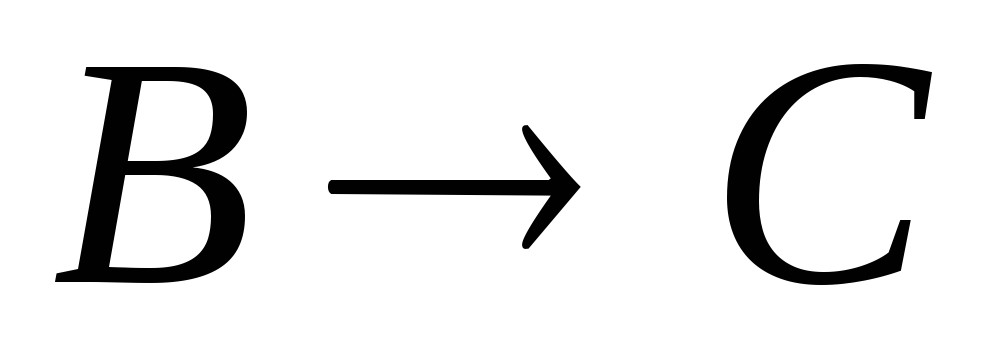 .
MP
2,1.
.
MP
2,1. .
MP 2,4.
.
MP 2,4.
3. Построить вывод формулы.
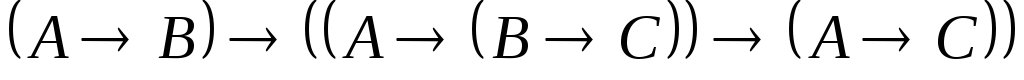 .
. .
.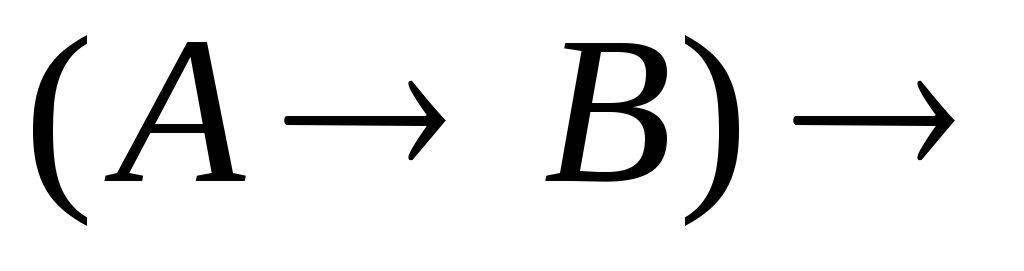
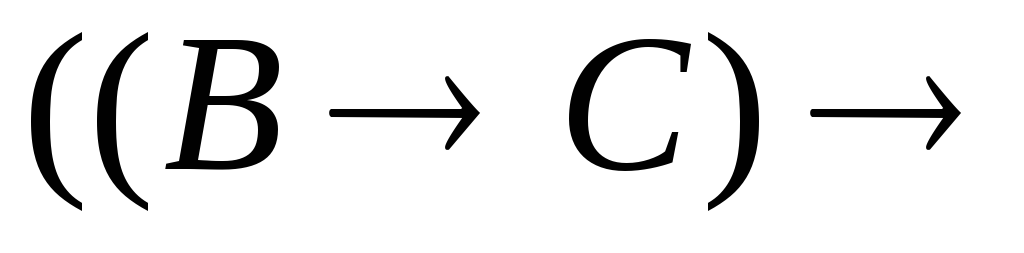

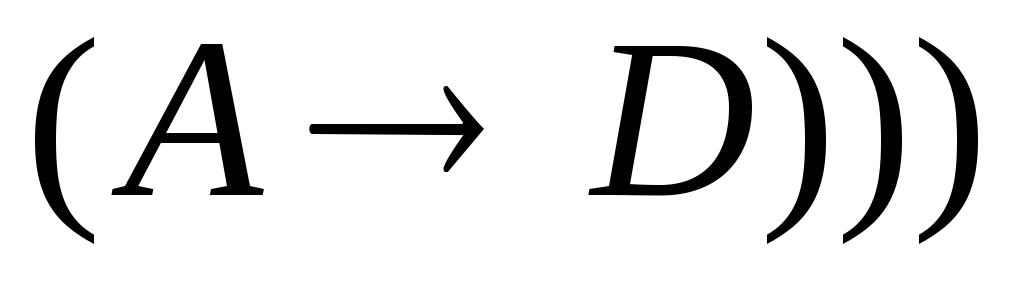 .
.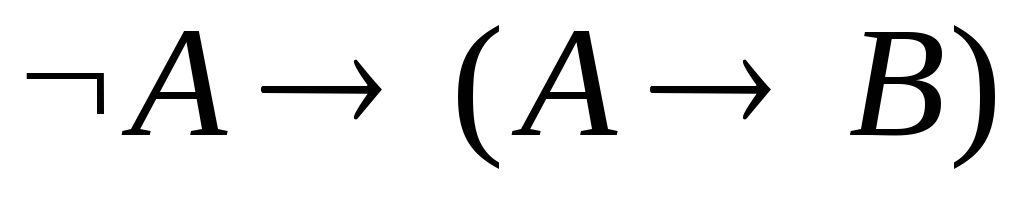 .
.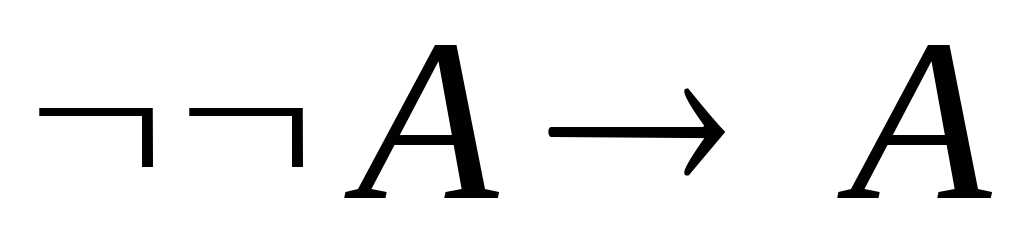 .
.
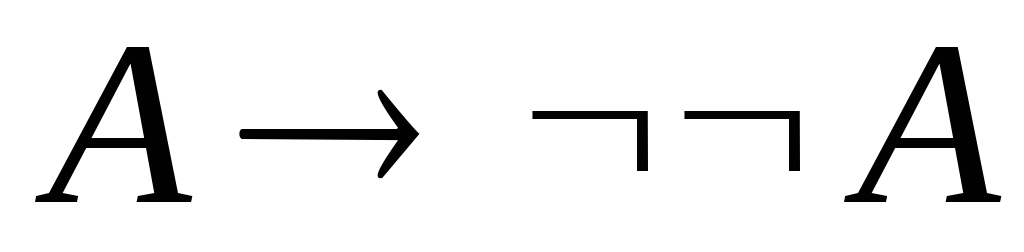 .
.
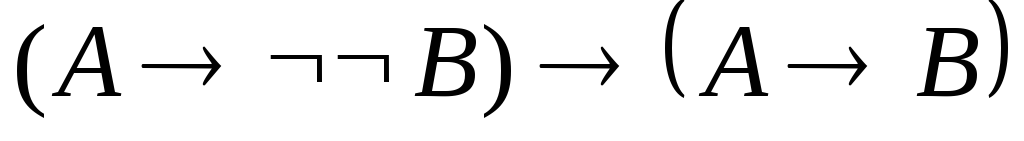 .
.
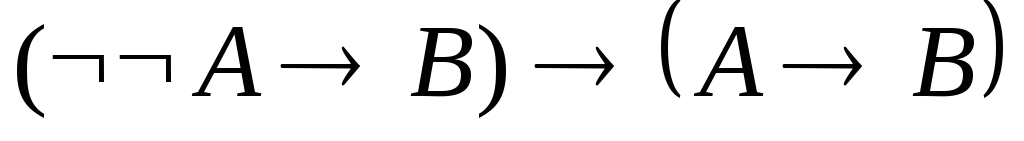 .
.
 .
.
 .
.
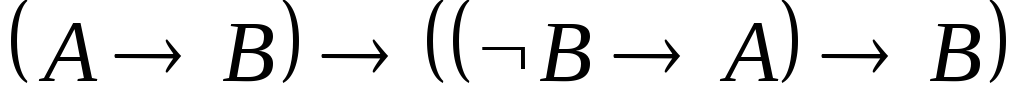 .
.
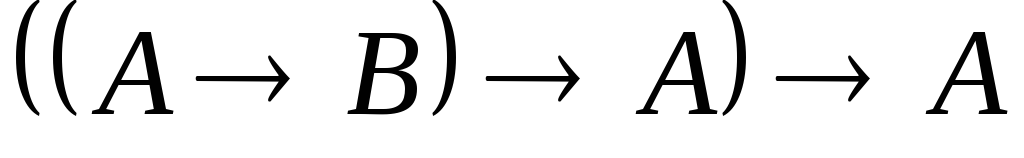 .
.
В Ответы и указания.
В Содержание.
