
- •Министерство Российской Федерации по связи и информатизации
- •Глава 1. Высказывания, формулы, тавтологии.
- •Отношения логической эквивалентности и логического следствия.
- •Задачи.
- •Глава 2. Формальные теории.
- •Глава 3. Исчисление высказываний.
- •Построение вывода в логике высказываний.
- •Задачи.
- •Глава 4. Метод резолюций в логике высказываний.
- •Задачи.
- •Глава 5. Предикаты.
- •Задачи.
- •Глава 6. Исчисление предикатов.
- •Теория равенства.
- •Формальная арифметика.
- •Теория частично упорядоченных множеств.
- •Задачи.
- •Глава 7. Алгоритмы.
- •Глава 8. Рекурсивные функции.
- •Задачи.
- •Глава 9. Машины Тьюринга.
- •Операции с машинами Тьюринга.
- •Принцип двойственности.
- •Способы композиции машин Тьюринга.
- •Задачи.
- •Ответы и указания.
Отношения логической эквивалентности и логического следствия.
Определение.
Формулы
![]() и
и![]() называются логически эквивалентными
тогда и только тогда, когда формула
называются логически эквивалентными
тогда и только тогда, когда формула![]() – тавтология.
– тавтология.
Замечание.
Формула
![]() – тавтология, если таблицы истинности
формул
– тавтология, если таблицы истинности
формул![]() и
и![]() совпадают.
совпадают.
Пример.
По законам де Моргана, логически
эквивалентны формулы
![]() и
и![]() ,
а также формулы
,
а также формулы![]() и
и![]() .
.
Теорема. Отношение логической эквивалентности является отношением эквивалентности.
Рефлексивность, симметричность и транзитивность данного отношения следуют из замечания.
Справедливы правило подстановки и правило замены.
Пусть
![]() и
и![]() – формулы, содержащие букву
– формулы, содержащие букву![]() ,
,![]() и
и![]() – формулы, полученные из формул
– формулы, полученные из формул![]() и
и![]() соответственно подстановкой вместо
буквы
соответственно подстановкой вместо
буквы![]() формулы
формулы![]() .
.
Правило
подстановки. Если
формула
![]() логически эквивалентна формуле
логически эквивалентна формуле![]() ,
то формула
,
то формула![]() логически эквивалентна формуле
логически эквивалентна формуле![]() .
.
Пусть
![]() – формула, в которой выделена некоторая
подформула
– формула, в которой выделена некоторая
подформула![]() ,
,![]() – формула, полученная из формулы
– формула, полученная из формулы![]() заменой
заменой![]() на некоторую формулу
на некоторую формулу![]() .
.
Правило
замены. Если
формулы
![]() и
и![]() логически эквивалентны, то логически
эквивалентны и формулы
логически эквивалентны, то логически
эквивалентны и формулы![]() и
и![]() .
.
Доказательства правил подстановки и замены основано на сравнении таблиц истинности соответствующих формул.
Пример.
Известна
тавтология
![]() (проверьте самостоятельно). По правилу
подстановки, формула
(проверьте самостоятельно). По правилу
подстановки, формула![]() логически эквивалентна формуле
логически эквивалентна формуле![]() .
По правилу замены, примененному к закону
двойного отрицания, получаем, что формула
.
По правилу замены, примененному к закону
двойного отрицания, получаем, что формула![]() логически эквивалентна формуле
логически эквивалентна формуле![]() .
Следовательно, по свойству транзитивности,
формулы
.
Следовательно, по свойству транзитивности,
формулы![]() и
и![]() логически эквивалентны.
логически эквивалентны.
Определение.
Говорят, что формула
![]() логически влечет формулу
логически влечет формулу![]() (из формулы
(из формулы![]() логически следует формула
логически следует формула![]() ),
если формула
),
если формула![]() является тавтологией.
является тавтологией.
Теорема. Отношение логического следствия является отношением предпорядка, то есть рефлексивным и транзитивным отношением.
Пример.
Формула
![]() логически влечет формулу
логически влечет формулу![]() .
В самом деле, в примере 1 предыдущего
пункта было доказано, что формула
.
В самом деле, в примере 1 предыдущего
пункта было доказано, что формула![]() является тавтологией.
является тавтологией.
В Содержание.
Задачи.
1. Установить, является ли предложение высказыванием, и если является, истинно оно или ложно.
Волга впадает в Каспийское море.
Студент второго курса.
 .
.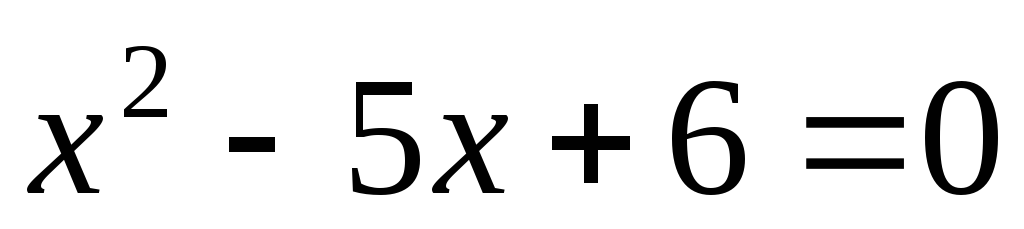 .
.Существует человек, который не старше своего отца.
 .
.Марс есть спутник Земли.
 .
. .
.Который час?
2. Установить, является ли предложение высказыванием, и если является, истинно оно или ложно.
 .
. .
. .
.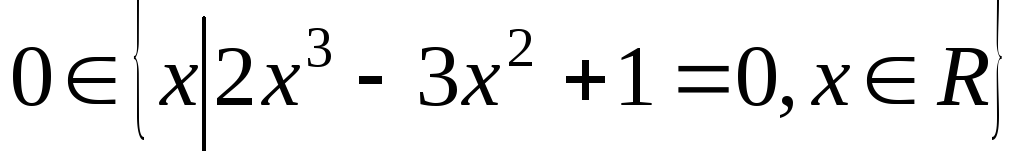 .
. .
. .
. .
. .
.
 .
.
 .
.
3. Среди следующих высказываний выделить элементарные и составные. В составных высказываниях обозначить элементарные высказывания буквами и записать с помощью логических символов.
Число 6 является делителем числа 36.
Число 225 делится нацело на 5.
Число 225 делится нацело на 5 и не делится на 10.
Если 81 делится нацело на 9, то 81 делится на 3.
16 кратно 2.
18 кратно 2 и 3.
 .
.Число 39 имеет 2 простых делителя.
Двузначное число 19 простое.
Корнями уравнения
 являются числа 2 и 3.
являются числа 2 и 3.
4.
Пусть
![]() обозначает высказывание“Я
увлекаюсь горным туризмом”, а
обозначает высказывание“Я
увлекаюсь горным туризмом”, а
![]() обозначает высказывание“Я
изучаю программирование”. Дайте
словесную формулировку следующих
высказываний:
обозначает высказывание“Я
изучаю программирование”. Дайте
словесную формулировку следующих
высказываний:
 ; 2)
; 2)
 ;
3)
;
3) ;
4)
;
4) ;
5)
;
5) ;
6)
;
6) ;
;
7)
![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ;
10)
;
10)![]() .
.
5. Проверить, является ли формула тавтологией, без построения таблицы истинности.
|
1)
|
6)
|
|
2)
|
7)
|
|
3)
|
8)
|
|
4)
|
9)
|
|
5)
|
10)
|
6. Доказать, что формула является тавтологией, без построения таблицы истинности. Во всех формулах выделить всевозможные подформулы.
 .
. .
. .
. .
. .
. .
. .
. .
.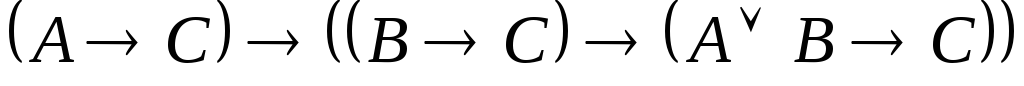 .
. .
.
Доказать, что формулы логически эквивалентны.
 и
и
 .
. и
и
 .
. и
и
 .
. и
и
 .
. и
и
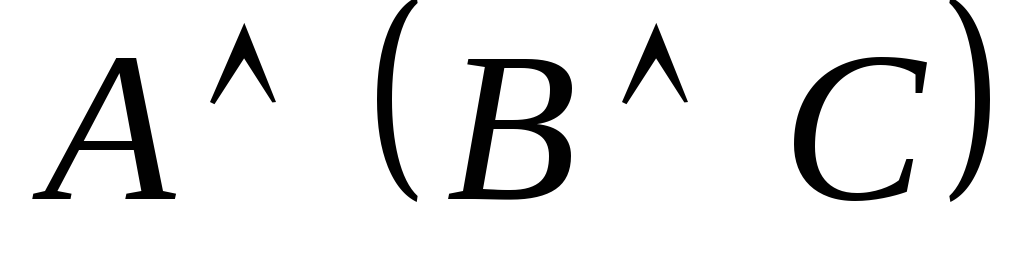 .
. и
и
 .
. и
и
 .
. и
и
 .
. и
и
 .
. и
и
 .
.
Доказать, что первая формула логически влечет вторую формулу.
 ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
. ;
;
 .
.
9. Доказать теорему о том, что отношение логической эквивалентности является отношением эквивалентности.
10. Доказать теорему о том, что отношение логического следования является отношением предпорядка.
В Ответы и указания.
В Содержание.
