Задачи.

1. По заданной машине Тьюринга и начальной конфигурациинайти заключительную конфигурацию:

1. ; .

2. ; .

3. ; .

4. ;.

5. ; .

6. ; .

7. ; .

8. ; .

9. ; .

10. ; .

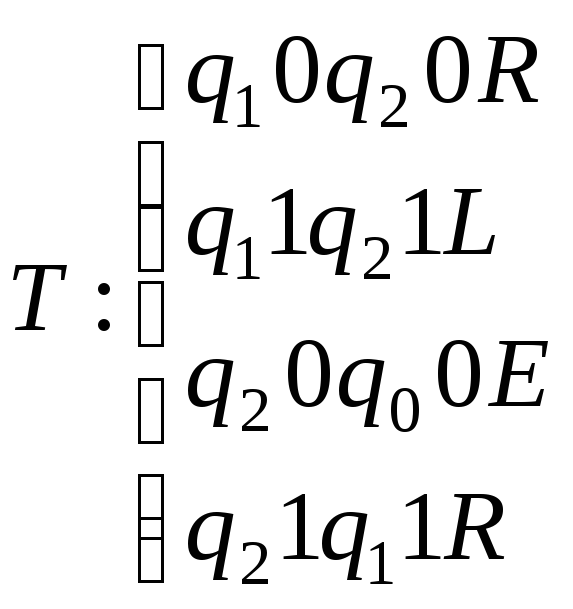2. Выяснить, применима ли машина Тьюринга к слову. Если применима, то записать результатприменения машинык слову. Предполагается, что в начальный момент времени головка машины обозревает самую левую единицу слова.

1) ; а); б).

2) ; а); б).

3. ; а) ; б).

4) ; а); б).

5) ; а); б).

3. Построить в алфавите {0,1} машину Тьюринга, обладающую свойствами:

1. машина имеет одно состояние, одну команду и применима к любому слову в алфавите {0,1};

2. машина имеет одно состояние, две команды, не применима ни к какому слову в алфавите {0,1}, и в процессе работы головка обозревает бесконечное множество ячеек;

3. машина имеет две команды, не применима ни к какому слову в алфавите {0,1}, и в процессе работы головка обозревает одну ячейку.

Предполагается, что в начальный момент времени головка машины обозревает самый левый символ слова.

4. По словесному описанию машины Тьюринга построить ее программу (в алфавите {0,1}).

1. Начав работу с первой единицы массива из единиц, машина “сдвигает” его на две ячейки вправо, не изменяя остального содержимого ленты, и останавливается на последней единице перенесенного массива.

2. Начав двигаться влево от произвольной ячейки, головка находит первую при таком перемещении ячейку с единицей (если такая встретится на пути) и, сделав один шаг вправо, останавливается на соседней ячейке. Содержимое ленты не меняется.

3. Машина начинает работу с самой левой непустой ячейки и отыскивает нуль, примыкающий с левой стороны к первому справа массиву из трех единиц, окаймленному нулями. Головка останавливается на первой единице найденного массива (если такой есть). Содержимое ленты не меняется.

4. Головка машины, начав работу с произвольной ячейки, содержащей единицу, двигается влево до тех пор, пока не пройдет подряд пять нулей. Головка останавливается на первой ячейке слева за этими пятью нулями, напечатав в ней единицу. Остальное содержимое ленты не меняется.

5. При заданном головка машины, начав работу с произвольной ячейки и двигаясь вправо, записывает подряднулей и останавливается на последнем из них.

6. Головка машины, двигаясь вправо от какой-либо пустой ячейки, находит первый при таком перемещении массив, содержащий не менее семи единиц, стирает в нем первые семь единиц и останавливается на самой правой из ячеек, в которых были стерты единицы. Остальное содержимое ленты не меняется.

7. При заданном значении n головка машины из n записанных единиц оставляет на ленте единицы, так же записанных подряд, если, и работает вечно, еслиили.

8. Машина реализует алгоритм вычисления функции , считая, что числоn представляется записанными подряд n единицами, и массив из n единиц уже найден.

9. Машина реализует алгоритм вычисления функции , считая, что числоn представляется записанными подряд n единицами, и массив из n единиц уже найден.

10. Машина реализует алгоритм вычисления функции

Считается, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.

11. Показать, что для всякой машины Тьюринга существует эквивалентная ей машина, в программе которой отсутствуют заключительные состояния.

12. Показать, что для всякой машины Тьюринга существует эквивалентная ей машина, в программе которой отсутствует символ E.

5. Для машин Тьюринга из задачи 1 построить двойственные машины.

6. Построить композицию машин Тьюрингаипо паре состояний (,) и найти результат применения композициик слову.

1)
:	0			, :	0
	1				1

а) ; б).

2)
:	0
	1

:	0
	1

а) ; б).

3)
:	0
	1			-

:	0
	1

а) ; б).

7. Найти результат применения итерации машины по паре состояний (,) к слову(заключительными состояниями являютсяи).

:	0
	1				-	-

а) ; б).

:	0
	1

а) ; б).

В Ответы и указания.

В Содержание.