Операции с машинами Тьюринга.

Очевидно, что некоторые алгоритмы могут быть составлены из нескольких более простых алгоритмов, и наоборот, могут служить основой для построения новых алгоритмов.

Точно также, удобно строить машины Тьюринга, исходя из уже построенных машин.

Принцип двойственности.

Пусть Т – произвольная программа (машина Тьюринга). Обозначим Т* программу, которая получается из Т заменой (во всех командах) R на L и наоборот. Программа Т* называется двойственной к Т.

Пример. Машина Тьюринга в произвольной записи, начиная с любой ячейки, двигаясь вправо, находит первый нуль. Соответствующая программа имеет вид:

.

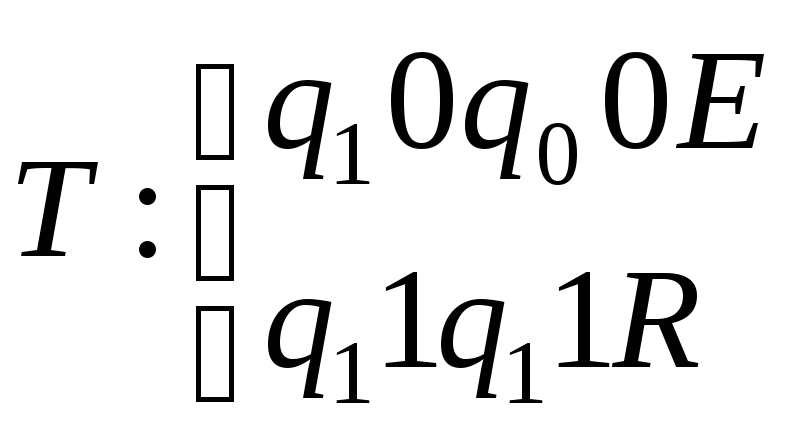Возможны три случая.

1. В начальный момент головка машины обозревает нуль. Машина останавливается.

2. В начальный момент головка машины обозревает единицу, и справа от начальной ячейки есть хотя бы один нуль. Машина переместит головку через массив единиц вправо и остановится перед первым нулем.

3. В начальный момент головка машины обозревает единицу, и справа от начальной ячейки запись состоит только из единиц. Машина будет перемещать головку через массив единиц вправо, не останавливаясь.

В программе заменим символ R на L. Получим программу:

.

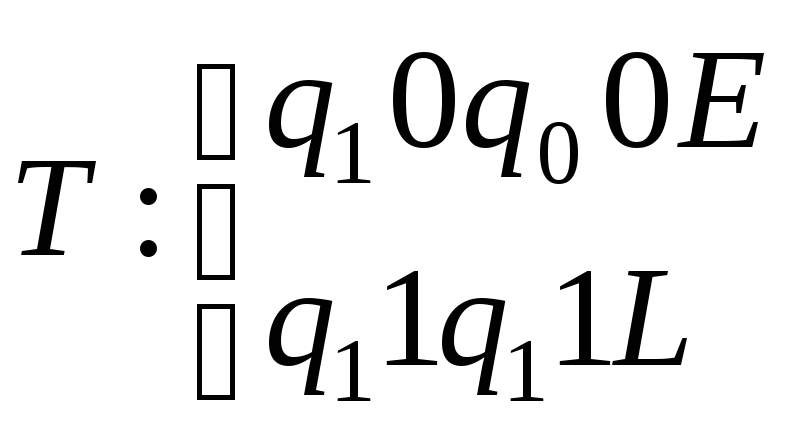Данная программа будет двойственной к предыдушей. Непосредственной проверкой можно убедиться, что головка машины, двигаясь влево, будет отыскивать первый нуль.

Очевидно, что (Т*)*=Т, то есть понятие двойственности является взаимным. Машины Тьюринга, соответствующие двойственным программам, будем называть двойственными машинами Тьюринга.

Из примера было видно, что двойственные машины функционируют симметричным образом. Так, пусть в начальный момент времени имеется конфигурация

,

и машина Т в момент времени t переработает ее в конфигурацию

.

В то же время, двойственная машина Т* конфигурацию

(симметричную первой конфигурации относительно ) в момент времениt переработает в конфигурацию

,

симметричную второй конфигурации относительно .

В Содержание.

Способы композиции машин Тьюринга.

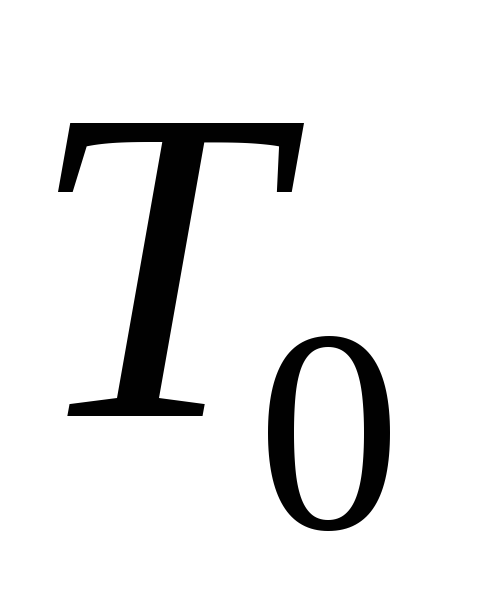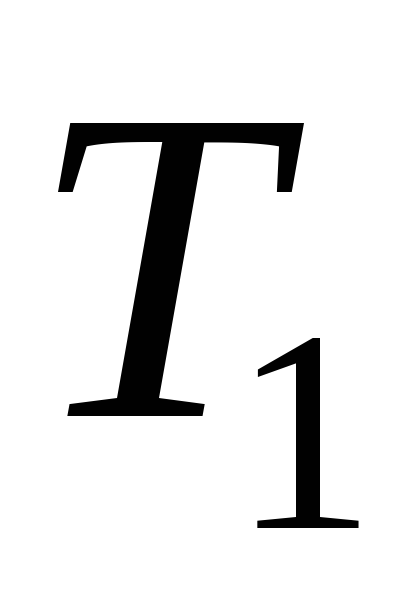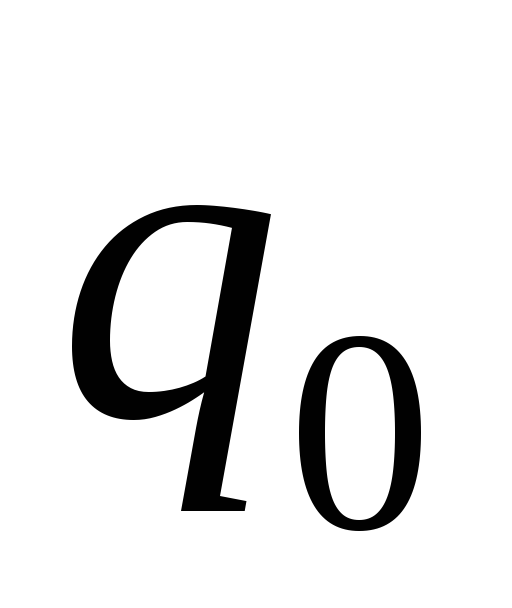1. Последовательное подключение одной машины Тьюринга к другой. Пусть и– две машины Тьюринга над алфавитом{0,1}, множества состояний машин не пересекаются. Перенумеруем 0,1,…,l-1 все команды с программы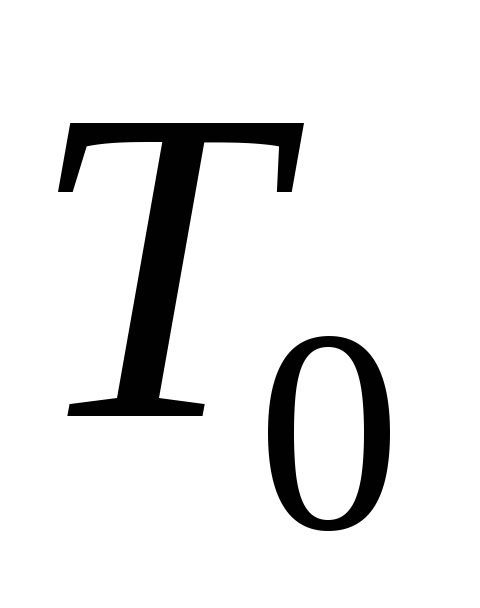. Пустьp(x) – предикат на множестве {0,1,…,l-1}. Последовательное подключение 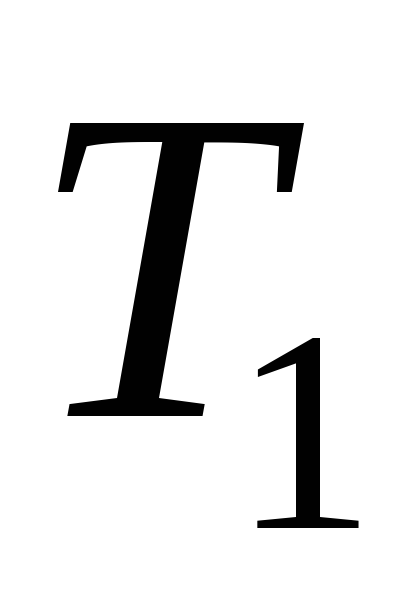к 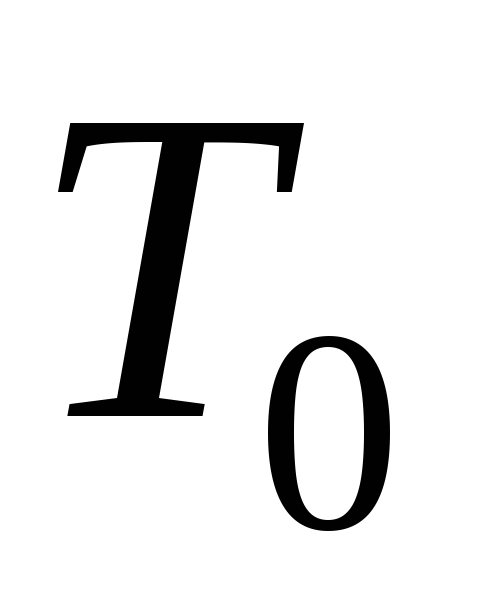(относительно предикатаp(x)) – это машина Тьюринга , которая получается следующим образом. 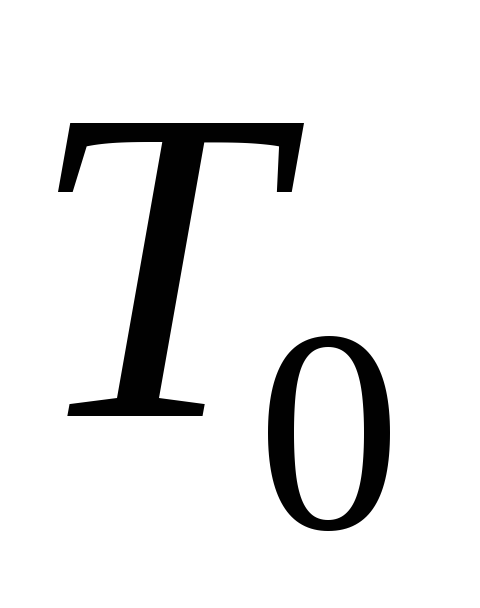Первая половина таблицы длясовпадает с таблицейдля тех клеток, в которых нет команды с.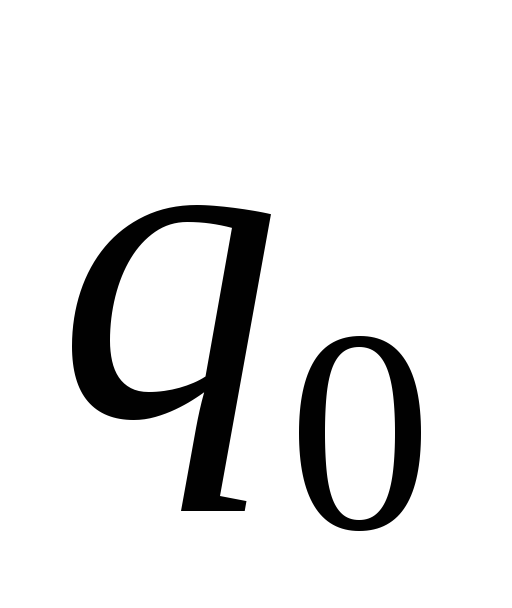

Если p(n)=1, то в клетке n – команда ,– номер строки (0 или 1), где находится клеткаn, – начальное состояние.

Если p(n)=0, то в клетке n – команда с . Вторая половина таблицыТ полностью совпадает с таблицей .

	……	……
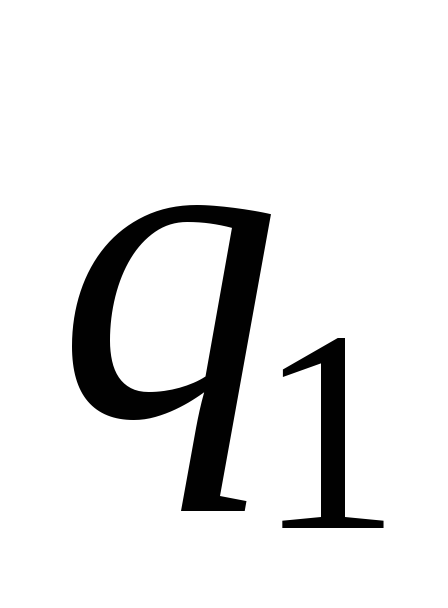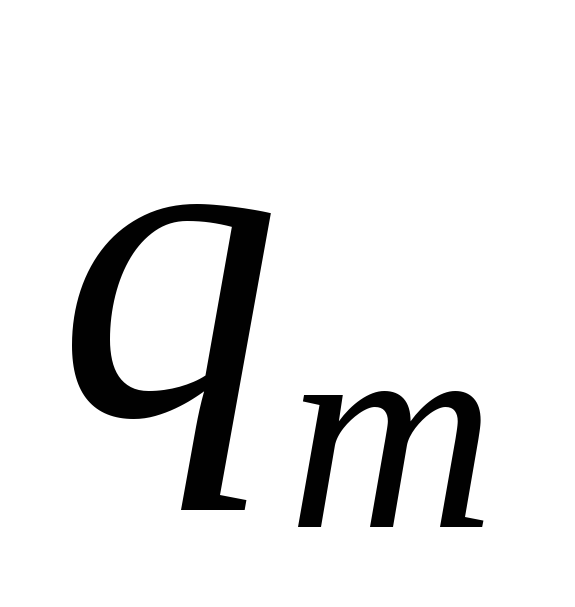
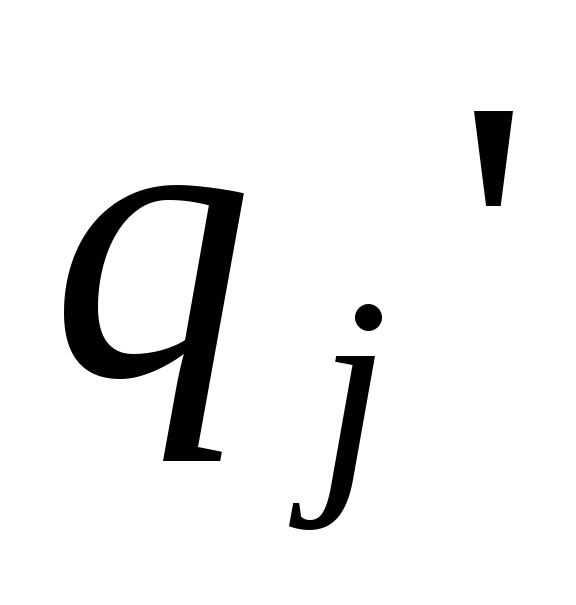0
1

В частном случае, если – начальное состояние машины, а– начальное состояние, заменим в программесостояниена состояние, и полученную программу объединим с программой. В результате мы получим программу для машины, которая является композицией машинипо паре состояний (,).

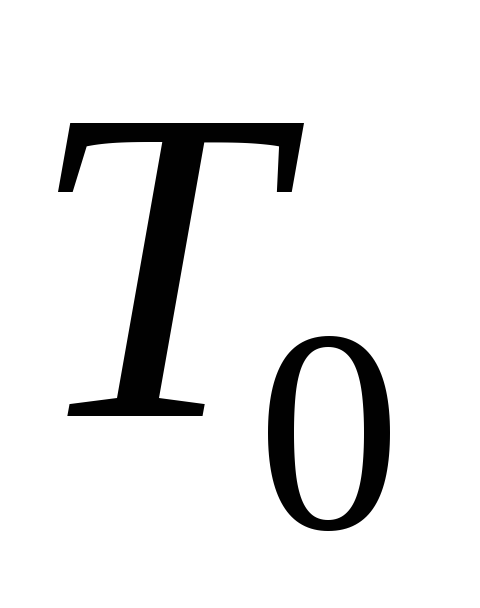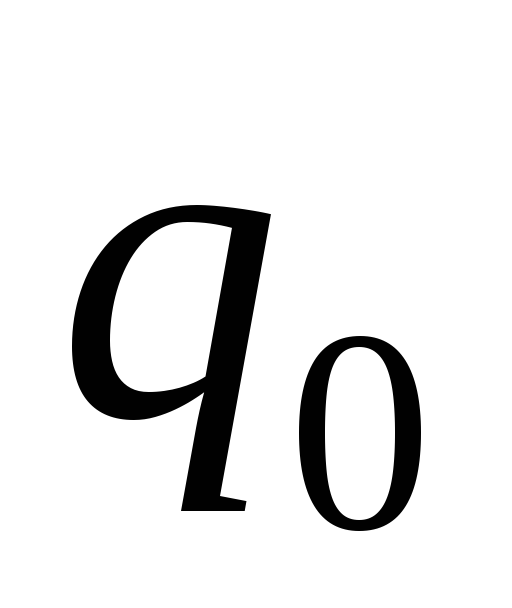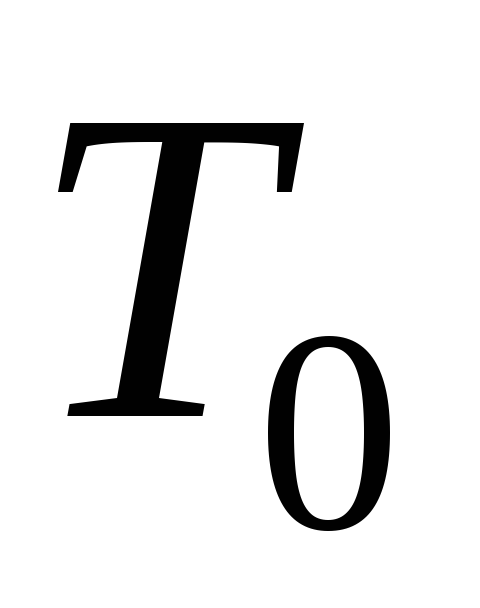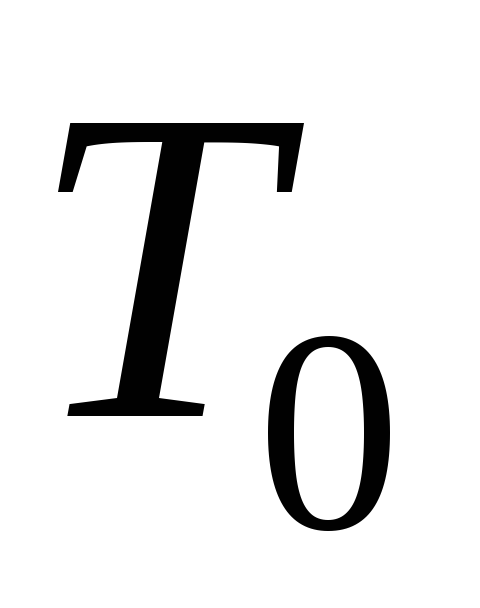2. Итерация машины Тьюринга. Пусть – машина Тьюринга над алфавитом{0,1}. Перенумеруем 0,1,…,l-1 все команды с программы. Пустьp(x) – предикат на множестве {0,1,…,l-1}. Итерация машины Тьюринга относительно предикатаp(x) – это машина Тьюринга Т, которая получается следующим образом. Таблица Т совпадает с таблицей для тех клеток, в которых нет команды не с.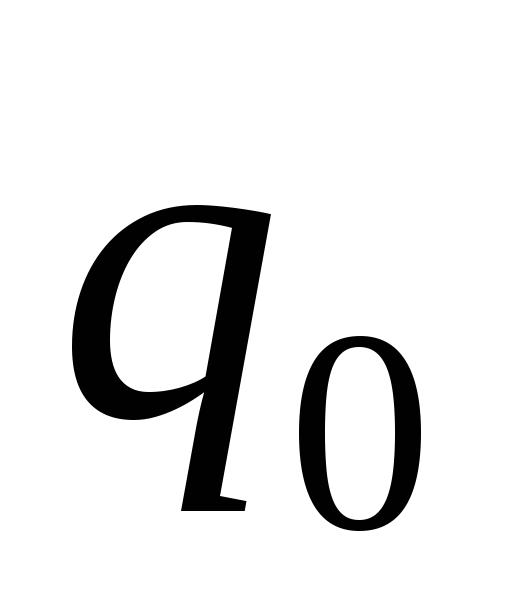

Если p(n)=1, то в клетке n – команда ,a – номер строки, где находится клетка n, – начальное состояние.

Если p(n)=0, то в клетке n – команда с .

Действительно, имеет место итерация, т.е. многократная работа машины .

В частном случае, если – заключительное состояние машины, а– любое состояние машины, не являющееся заключительным, то заменим в программесостояниена состояние. В результате мы получим программу для машиныТ, которая является итерацией машины по паре состояний (,).

Отметим, что начальных и заключительных состояний может быть несколько.

В Содержание.