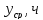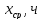- •Расчет показателей надежности элементов системы электроснабжения
- •Модель отказов и восстановления генератора
- •Модель отказов и восстановления силового трансформатора
- •Модель отказов и восстановления воздушной линии электропередачи
- •Модель отказов и восстановления подстанционного оборудования
- •Расчет надежности системы электроснабжения

Содержание
Задание………………………………………………………………………….…4
Введение…………………………………………………………………………...5
1 Расчет показателей надежности элементов системы электроснабжения..6
1.1 Модель отказов и восстановления генератора…………………………….6
1.2 Модель отказов и восстановления силового трансформатора……………7
1.3 Модель отказов и восстановления воздушной линии электропередачи..11
1.4 Модель отказов и восстановления подстанционного оборудования…...14
2 Расчет надежности системы электроснабжения………………………….19
Заключение……………………………………………………………………….21
Список литературы………………………………………………………………22
Задание
Система электроснабжения двух энергорайонов, питающихся от одного источника Г с повышающим трансформатором Т, представлена на рисунке 1. Энергорайоны № 1 и № 2 получают питание, соответственно, по воздушным линиям электропередач ВЛ1 и ВЛ2 от подстанций А,Б,В.
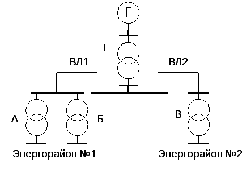
Рисунок 1 – Схема системы электроснабжения
Энергорайон № 1 получает электропитание через две подстанции А и Б, соединенных параллельно по низкой стороне. Подстанция А или Б способны в отдельности обеспечить электропитание данного энергорайона. В связи с этим нарушение электроснабжения энергорайона №1 наступает только при одновременном обесточивании подстанций А и Б.
Энергорайон №2 подключен через подстанцию В и обесточивается при всех возможных отказах, ведущих к обесточиванию этой подстанции.
Введение
Проблема надежности системы электроснабжения является одной из первоочередных проблем энергетики.
Аварийные и внезапные перерывы электроснабжения потребителей вызывают большой народнохозяйственный ущерб, обусловленный выходом из строя оборудования, порчей сырья и материалов, затратами на ремонты, недовыпуском продукции, простоями технологического оборудования и рабочей силы, а также издержками, связанными с другими факторами.
Сегодня методы анализа надежности используются уже во многих отраслях техники. Однако проблема надежности в ее количественной постановке при проектировании и эксплуатации систем электроснабжения необыкновенно сложна. Так, для рассмотрения вопросов надежности при эксплуатации систем электроснабжения необходимо учесть как современные достижения теории надежности, так и специфику функционирования систем силового типа, подверженных в значительной степени влиянию неблагоприятных воздействий внешней среды и непосредственно связанных с электрической системой.
Целью данной работы является расчет надежности электрооборудования простейшей системы электроснабжения и связанная с эти надежность бесперебойного обеспечения потребителей электроэнергией.
-
Расчет показателей надежности элементов системы электроснабжения
-
Модель отказов и восстановления генератора
Отказы генераторов складываются из внезапных и постепенных отказов. В случае отсутствия данных о наработке по этим отказам и при условии, что все календарное время года, кроме времени восстановления, генератор находится в состоянии работы, можно использовать статистику за последние L лет о числе случаев обесточивания генератора nj и длительности его пребывания τi при i-ом обесточенном состоянии представленную в таблице 1.
Таблица 1 – Статистические данные времени восстановления генератора за последние десять лет эксплуатации
|
восстановления |
||||
|
106,5 |
154,3 |
112,1 |
78,5 |
|
|
49,3 |
86,4 |
55,3 |
168,5 |
|
|
121,4 |
57,6 |
65,1 |
124,6 |
|
|
78,6 |
79,7 |
132,1 |
85,4 |
|
|
63,5 |
147,5 |
87,3 |
51,6 |
|
|
|
|
|||
Среднее
время пребывания генератора в состоянии
отказа (обесточивания)
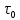 и среднее время пребывания генератора
в состоянии отказа в течение года
находится по формуле:
и среднее время пребывания генератора
в состоянии отказа в течение года
находится по формуле:
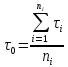 ,
час;
,
час;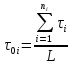 ,
час/год. (1)
,
час/год. (1)
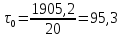 час;
час;
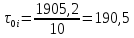 час/год.
час/год.
Среднее
время пребывания генератора в
работоспособном состоянии в течении
года
 определяется по формуле:
определяется по формуле:
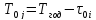 ,
(2)
,
(2)
где
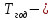 календарное число часов в расчетном
периоде (один расчетный год равен 8760
часов).
календарное число часов в расчетном
периоде (один расчетный год равен 8760
часов).
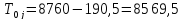 часов.
часов.
Коэффициент готовности вычисляется по формуле:
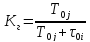 ,
(3)
,
(3)
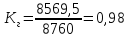 .
.
Для стационарного режима работы системы с восстановлением коэффициент готовности можно принять за вероятность безотказной работы. В этом случае вероятность безотказной работы генератора можно выразить:
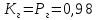 .
.
-
Модель отказов и восстановления силового трансформатора
Трансформатор можно условно рассматривать как объект, состоящий из двух последовательно соединенных элементов, в одном из которых могут появляться внезапные отказы, а в другом постепенные. Внезапные отказы связаны с повреждениями вводов трансформатора вследствие перекрытия контактных соединений, утечкой масла и др. Постепенные отказы вызваны износом изоляции обмоток вследствие возникновения внешних и внутренних перенапряжений, сквозных токов коротких замыканий и дефектов изготовления.
Вероятность безотказной работы трансформатора представим произведением вероятностей:
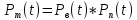 ,
(4)
,
(4)
где
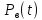 и
и
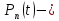 соответственно вероятности безотказной
работы, соответствующие внезапному и
постепенному отказу.
соответственно вероятности безотказной
работы, соответствующие внезапному и
постепенному отказу.
В теории надежности основным законом времени безотказной работы при внезапных отказах является показательное распределение:
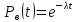 ,
(5)
,
(5)
где
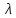 и
и
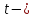 соответственно интенсивность внезапных
отказов и наработка.
соответственно интенсивность внезапных
отказов и наработка.
Постепенные отказы трансформатора происходят в основном по причине износа изоляции. Наиболее универсальным распределением, описывающим износные процессы, является трехпараметрический закон Вейбулла:
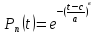 ,
(6)
,
(6)
где
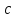 ,
,
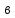 ,
,
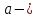 параметры распределения, удовлетворяющие
условиям:
параметры распределения, удовлетворяющие
условиям:
 .
.
Окончательно имеем:
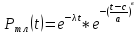 .
(7)
.
(7)
Таблица
2 – Статистический ряд наработки на
отказ внезапных
 и постепенных
и постепенных
 отказов силового трансформатора
отказов силового трансформатора
|
|
|
|
|
|
|
|
60247 |
77689 |
55726 |
40269 |
61355 |
41356 |
|
61589 |
71720 |
49501 |
37205 |
40958 |
39026 |
|
78243 |
60528 |
54265 |
29124 |
36897 |
26056 |
|
54973 |
60024 |
59584 |
38562 |
39542 |
40958 |
|
59624 |
41589 |
40308 |
37268 |
40235 |
38380 |
|
57604 |
58206 |
61467 |
66248 |
51545 |
41145 |
|
74849 |
47901 |
48951 |
41608 |
36441 |
38429 |
|
58295 |
54807 |
60548 |
39796 |
38528 |
39484 |
|
|
|
61208 |
|
|
61057 |
|
|
|
λ2ТР, 1/ч |
|
|
λ1ТР, 1/ч |
|
58777,8 |
|
1,71*10-5 |
41673,3 |
|
2,4*10-5 |
Параметр показательного закона 1 находим по формуле:
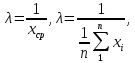 (8)
(8)
где
 среднее значение наработок на отказ.
среднее значение наработок на отказ.
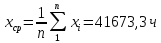 ;
;
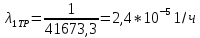 .
.
Среднее время безотказной работы при внезапных отказах трансформатора определим по формуле:
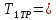
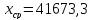 (9)
(9)
.
Оценим параметры трехпараметрического распределения Вейбулла, используемого при постепенных отказах трансформатора. Для этого вычислим среднее значение наработки на отказ:
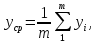 (10)
(10)
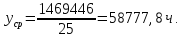
Среднеквадратическое отклонение σ наработки на отказ равно:
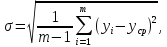 (11)
(11)
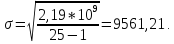
Вычислим
значение
 :
:
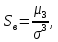 (12)
(12)
где
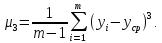
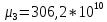 ;
;
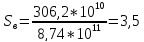 .
.
По
таблице приведенной в приложении 1,
через известное значение
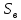 находим величину параметра
находим величину параметра
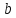 .
По этой же таблице находим значение
.
По этой же таблице находим значение
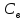 ,
используя которое определим величину
параметра
,
используя которое определим величину
параметра
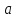 :
:
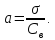

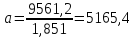 .
.
Определив
по таблице приложения 1 значение
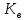 рассчитаем величину параметра
рассчитаем величину параметра
 :
:
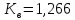 ;
;
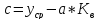 ;
(15)
;
(15)
 .
.
Среднее время безотказной работы при постепенных отказах принимается:
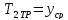 ;
(16)
;
(16)
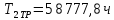 .
.
Средняя интенсивность постепенных отказов равна:
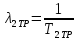 ;
(17)
;
(17)
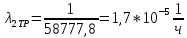 .
.
Результирующая интенсивность отказов силового трансформатора составляет:
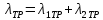 ;
(18)
;
(18)
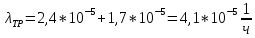 .
.
Интенсивность восстановления определим по данным статистического ряда.
Таблица
3 – Статистический ряд времени
восстановления
 внезапных и постепенных отказов силового
трансформатора
внезапных и постепенных отказов силового
трансформатора
|
Восстановление |
||||
|
25,7 |
18,6 |
23,4 |
14,4 |
|
|
31,4 |
14,9 |
39,2 |
45,7 |
|
|
24,5 |
20,7 |
18,6 |
38,6 |
|
|
27,6 |
23,8 |
17,9 |
20,3 |
|
|
49,3 |
24,4 |
46,6 |
21,6 |
|
|
|
|
|||
Среднее время безотказной работы силового трансформатора:

Среднее время восстановления силового трансформатора:
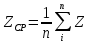 ;
;
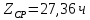 .
.
Результирующая интенсивность восстановления силового трансформатора:
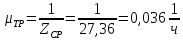 .
.
Коэффициент готовности силового трансформатора:
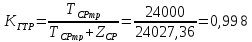 .
.
В стационарном режиме работы силового трансформатора коэффициент готовности будет вероятностью его безотказной работы.

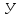 ,
ч
,
ч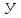 ,
ч
,
ч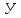 ,
ч
,
ч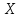 ,
ч
,
ч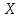 ,
ч
,
ч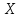 ,
ч
,
ч