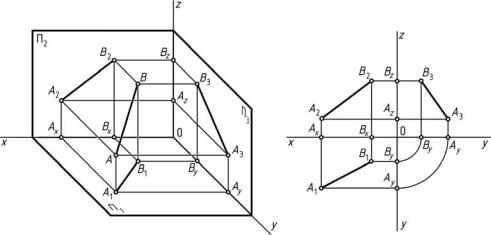
Простейшей линией является прямая линия. Она определяется в пространстве двумя точками, принадлежащими ей (рис. 10). На комплексном чертеже проекции прямой задаются проекциями этих точек.

Пусть заданы проекции точек пространства А и В: А1 — горизонтальная проекция точки А; А2 — фронтальная проекция точки А; В1 — горизонтальная проекция точки В; В2 — фронтальная проекция точки В. Соединив одноименные проекции точек А и В, получают проекции отрезка прямой АВ: А1В1 — горизонтальная проекция отрезка прямой АВ и А2В2 — фронтальная проекция отрезка прямой АВ. Для определения положения прямой в пространстве достаточно двух ее проекций. Третью проекцию, например, профильную А3В3, всегда можно определить по двум заданным

(см. рис. 10).

Рис. 10. Проекции прямой линии

3.2. Прямые общего и частного положения

Прямая линия может занимать произвольное положение относительно плоскостей проекций.

Прямая, непараллельная и неперпендикулярная ни одной из плоскостей проекций, называется прямой общего положения (см. рис. 10). Проекции прямой общего положения произвольно наклонены к осям проекций и на эпюре Монжа составляют с координатными осями произвольные углы наклона.

Прямые, параллельные или перпендикулярные каким-либо плоскостям проекций, называются прямыми частного положения.

Различают:

прямые уровня — прямые, параллельные одной какой-либо плоскости проекций;

проецирующие прямые (дважды параллельные) — прямые, пер-

пендикулярные одной какой-либо плоскости проекций и параллельные двум другим плоскостям проекций одновременно.

27

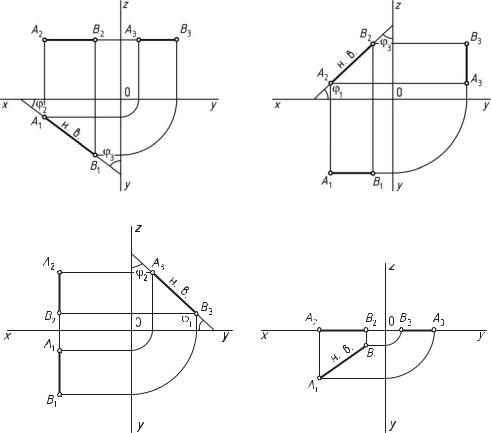
Прямые уровня.

1. Горизонтальная прямая уровня — прямая, параллельная гори-

зонтальной плоскости проекций П1 (рис. 11, а). На данную плоскость проекций прямая проецируется в натуральную величину и составляет углы наклона ϕ2 к фронтальной плоскости проекций П2 и ϕ3 к профильной плоскости проекций П3.

2. Фронтальная прямая уровня — прямая, параллельная фрон-

тальной плоскости проекций П2 (рис. 11, б). На данную плоскость проекций прямая проецируется в натуральную величину и составляет углы наклона ϕ1 к горизонтальной плоскости проекций П1 и ϕ3 к профильной плоскости проекций П3.

3. Профильная прямая уровня — прямая, параллельная профильной плоскости проекций П3 (рис. 11, в). На данную плоскость проекций прямая проецируется в натуральную величину и составляет углы наклона ϕ1 к горизонтальной плоскости проекций П1 и ϕ2 к фронтальной плоскости проекций П2.

Рис. 11. Проекции прямых уровня

28