
- •ОГЛАВЛЕНИЕ
- •ПРЕДИСЛОВИЕ
- •ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
- •ВВЕДЕНИЕ
- •Тема 1. Метод проекций
- •1.1. Предмет начертательной геометрии
- •1.2. История развития начертательной геометрии
- •1.3. Методы проецирования
- •Тема 2. Проекции точки
- •2.1. Проекции точки на три плоскости проекций. Координатный способ задания объекта на чертеже
- •2.2. Метод конкурирующих точек
- •Тема 3. Проекции прямой
- •3.1. Линии. Кривая линия. Комплексный чертеж прямой
- •3.2. Прямые общего и частного положения
- •3.3. Следы прямой
- •3.5. Относительное расположение прямых линий
- •Тема 4. Проекции плоскости
- •4.1. Способы задания плоскости на комплексном чертеже
- •4.2. Следы плоскости
- •4.3. Плоскости общего и частного положения
- •4.4. Принадлежность точки и прямой плоскости
- •4.5. Главные линии плоскости
- •4.6. Относительное расположение плоскостей
- •4.7. Относительное расположение прямой и плоскости
- •Тема 5. Способы преобразования проекций
- •5.1. Общие сведения
- •5.2. Способ замены плоскостей проекций
- •5.3. Способ вращения
- •Способ вращения вокруг оси, параллельной плоскости проекций (вращение вокруг линии уровня).
- •Тема 6. Поверхности
- •6.2. Классификация поверхностей
- •I. Линейчатые поверхности
- •II. Нелинейчатые поверхности
- •I. Линейчатые поверхности вращения
- •Тема 7. Пересечение поверхности плоскостью
- •7.1. Общие понятия и определения
- •7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения
- •7.3. Сечения геометрических тел плоскостями общего положения. Определение натуральной величины сечения
- •Тема 8. Пересечение поверхности прямой линией
- •Тема 9. Взаимное пересечение поверхностей
- •9.1. Взаимное пересечение поверхностей. Основные способы построения линий пересечения поверхностей
- •9.2. Способ вспомогательных секущих плоскостей
- •Пересечение гранных поверхностей
- •Пересечение гранных поверхностей и поверхностей вращения
- •9.3. Способ вспомогательных шаровых поверхностей
- •Тема 10. Проекции с числовыми отметками
- •10.1. Сущность способа проекций с числовыми отметками. Точка и прямая в проекциях с числовыми отметками
- •10.2. Плоскость в проекциях с числовыми отметками
- •10.3. Поверхность в проекциях с числовыми отметками
- •10.4. Топографическая поверхность
- •10.5. Пересечение прямой линии и плоскости c топографической поверхностью
- •10.6. Примеры решения инженерных задач
- •Тема 11. Аксонометрические проекции
- •11.1. Виды аксонометрических проекций
- •11.3. Окружность в аксонометрии
- •11.4. Аксонометрические проекции геометрических тел
- •Контрольная работа 1
- •Лист 1
- •Лист 2
- •Лист 3
- •Лист 4
- •Лист 5
- •Контрольная работа 2
- •Лист 6
- •Лист 7
- •Лист 8
- •Лист 9
- •ЗАКЛЮЧЕНИЕ
- •Список рекомендуемой литературы
Тема 6. Поверхности
6.1. Поверхности в технике и строительстве. Образование поверхности и ее задание на чертеже. 6.2. Классификация поверхностей.
6.3.Многогранники. Образование поверхностей некоторых многогранников. Точки на поверхности гранных геометрических тел. Общие принципы построения разверток гранных поверхностей.
6.4.Поверхности вращения. Образование некоторых поверхностей вращения. Точки на поверхности геометрических тел вращения. Общие принципы построения разверток поверхностей вращения
6.1. Поверхности в технике и строительстве. Образование поверхности и ее задание на чертеже
Мир поверхностей многогранен и безграничен. Он простирается от элементарных, простых до сложнейших, причудливых форм поверхностей и их сочетаний. По разнообразию форм и свойств, по той роли, которую они играют в науке, технике, строительстве, архитектуре, поверхности не имеют себе равных среди других геометрических образов.
С точки зрения начертательной геометрии многое из того, что нас окружает — это линии и поверхности простых и сложных форм, и все, что создается человеком (конструкции, объекты, сооружения и т. д.), ограничивается этими поверхностями.
Поверхность в начертательной геометрии определяется как непре-
рывное множество последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону и называемой образующей поверхности.
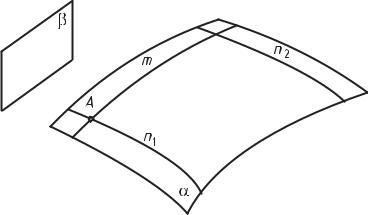
Обязательным условием перемещения образующей в пространстве при образовании поверхности является пересечение ее с неподвижными линиями пространства, называемыми направляющими поверхности. Кроме этого должен быть указан характер движения образующей по направляющим. На рис. 56 показан процесс образования некоторой поверхности. В качестве образующей взята плоская кривая линия m, которая скользит по двум направляющим n1 и n2, оставаясь, все время параллельной плоскости β. Точка A, принадлежащая образующей m, перемещается по кривой n1. Такой способ образования поверхности называется кинематическим, и он позволяет задать любую поверхность Ф определителем. Определителем поверхности называется необходимая и достаточная совокупность геометрических фигур и связей между ними, которые однозначно задают (определяют) поверхность Φ.
Определитель поверхности Φ может быть записан в виде структурной формы: Φ (Г), [А], где (Г) — геометрическая часть определителя, т. е. перечисление геометрических фигур, которые образуют поверхность; [А] — алгоритмическая часть определителя, устанавли-
67
вающая связь между этими фигурами. Для того чтобы определитель относился к конкретному виду поверхности, каждая часть определителя должна иметь конкретное содержание.
Рис. 56. Кинематический способ образования поверхности
На рис. 57 показано образование некоторых поверхностей в начертательной геометрии кинематическим способом:
призматической поверхности — прямая образующая m перемеща-
ется по ломанной направляющей n, сохраняя параллельность заданному направлению S (рис. 57, а);
цилиндрической поверхности — прямая образующая m перемеща-
ется по кривой направляющей n, сохраняя параллельность заданному направлению S (рис. 57, б);
пирамидальной поверхности — прямая образующая m перемеща-
ется по ломанной направляющей n, проходя через постоянную точку (вершину) S (рис. 57, в);
конической поверхности — прямая образующая m перемещается по кривой направляющей n, проходя через постоянную точку (верши-
ну) S (рис. 57, г).
На чертеже поверхность может быть задана:
определителем поверхности (например, проекциями образующих и направляющих);
каркасом — упорядоченное множество точек или линий, принадлежащих поверхности. Каркас может быть точечным и линейным. Точечным каркасом называют совокупность точек на поверхности, достаточно точно определяющих эту поверхность. Линейным каркасом называют совокупность линий, имеющих единый закон образования и связанных между собой определенной зависимостью. Для получения линейного каркаса поверхность пересекается параллельными плоскостями, линии пересечения которых с поверхностью и образуют ее каркас;
68
