ТПС / Лекции / Лекция 9

Лекция 9

Теория потенциальной помехоустойчивости: введение

В теории связи есть несколько важных задач: повышение пропускной способности, увеличение многоканальности и др. При организации связи по металлическому кабелю, по радиоканалу особенно актуальна задача повышения помехоустойчивости системы. Общее определение помехоустойчивости следующее. Помехоустойчивость это способность системы связи противостоять воздействию помех. Речь идет, прежде всего, о помехах электрического характера. Оценить помехоустойчивость можно по допустимому отношению сигнал/помеха, при котором система связи нормально функционирует. Критерием же нормальной работы служит чаще всего заданная вероятность ошибки приемника при приеме одного бита информации или слова для цифровой системы передачи (рис. 1).

Рис. 1 Структурная схема приемника.

В случае аналоговой передачи критерием является среднеквадратичная ошибка: 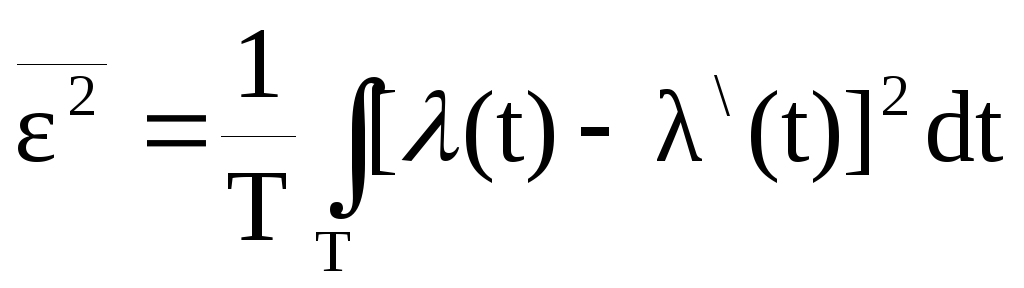, где T-длительность сообщения, и -переданное и принятое сообщения.

Помехи воздействующие на сигнал по разному взаимодействуют с ним . При аддитивная помеха сигнал на входе приемника определяется как , а при мультипликативной помеха . Как следует из рис. 1, помехоустойчивость определяется схемами демодулятора ДМ и декодера канала (помехоустойчивостью кода). В дальнейшем мы будем рассматривать только демодулятор.

Предельно достижимая помехоустойчивость приемника (демодулятора) называется потенциальной помехоустойчивостью. Она обеспечивается схемой оптимального приемника.

Помехоустойчивость зависит от схемы приемника, который в общем случае состоит из двух блоков (рис. 2): устройство оптимальной обработки УОО и решающее устройство РУ .

РУ

z(t)

λ′ – принятое сообщение

y(t)

УОО

Рис.2 Схема приемника (демодулятора)

Над принятым приемное устройство выполняет некоторую операцию U[^.] и на выходе имеем оценку сообщения `=U[y(t)]. Чтобы принять оценку необходимо руководствоваться определенным правилом решения, которое реализуется в решающем устройстве РУ.

Регулярное правило решения означает что принятому y(t) соответствует определенная оценка `.

Статистическое правило решения - ` и y(t) связаны статистически, то есть данному y(t) соответствует с какой-то вероятностью P(`).

Устройство оптимальной обработки УОО в общем случае должно вычислять по входному сигналу некоторую функцию по которой принимается решение о переданном сообщении. Существуют два метода обработки приходящего сигнала.

При линейной обработки над сигналом y(t) производится линейная операция. Как будет доказано в дальнейшем, чаще всего при этом вычисляется функция , где φ(t) – некоторый временной функционал. При такой процедуре повышается отношение сигнал-помеха к моменту принятия решения.

При нелинейной обработке сигнал на выходе УОО , где

V[y(t)] – нелинейный функционал. Такое преобразование может давать ограничитель напряжения, детектор и др.

Прием сигналов как статистическая задача

Сигнал на входе приемника всегда случаен, так как случайна помеха взаимодействующая с ним. Будем считать, что передаваемый сигнал за время существования Т строго определен, то есть детерминирован. Тогда его положение в многомерном пространстве можно представить вектором с нормой S_i (рис. 3).

β₁

S₁

β₀

S₀

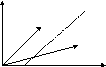
Рис.3 Векторное представление сигнала

Помеха в пространстве представляется случайным вектором n(t) находящимся в какой то области. Естественно, что после наложения ее на сигнал образуется некоторая случайная сумма и вектор имеет норму также расположенную в области. На рис.4 это показано на примере двух сигналов на входе приемника.

Рис.4. сигналы на входе приемника.

Случайность принимаемых сигналов позволяет привлечь к анализу статистические законы, это W(y/S_i) – условный закон распределения плотности вероятности приема сигнала при условии передачи i-го сигнала или более кратко функция правдоподобия.

Будем считать, что множество точек в пространстве образуют пространство принимаемого сигнала Y. Принимая сигналы y(t) приемник должен решить, какой сигнал был передан. Для этого все Y необходимо поделить на области. В нашем примере это β₀ и β₁. Если у попал в область β₀, то следует выносить решение в пользу S_0, если в β₁- S₁. Очевидно, что вероятность правильного приема будет определятся интегралом , вероятность ошибки , при i≠j. При множестве сигналов будем иметь множество областей β_i (рис. 5).

{y} – пространство принимаемого сигнала

β₀

β₁

β₂

β₄

β₃

Рис. 5 Области сигналов в пространстве.

Возникает вопрос, как назначать эти области? Здесь имеется некоторая неоднозначность. При увеличении одной из них, _i, увеличивается вероятность правильного приема данного сигнала, но одновременно с этим уменьшаются эти же вероятности для других, соседних, сигналов. К тому же растут вероятности ошибочного попадания в эту область. Из этого следует вывод о том, что области в пространстве должны быть выбраны по определенным правилам, которые называются критериями оптимального приема. В их основе отражается одна из задач приема: обнаружение сигнала, различение сигнала, восстановление сигнала. Первые две применяются в дискретных каналах связи, последняя в аналоговых системах.

Критерий минимального среднего риска.

В нем ставится задача различения сигнала. Введем функцию потерь J(λ,λ′), обладающую следующим очевидным свойством: J(λ,λ′)=0 при =` и J(λ,λ′)0 при `. Эта функция является случайной, поэтому введем W(λ,λ′) – двумерную плотность распределения переданного и принятого сообщений.

Найдем среднее значение функции потерь , это и будет средний риск средний риск.

. (1)

При регулярном правиле решения принятому сигналу жестко соответствует вынесенная оценка , поэтому в статистиках аргумент ` может быть заменен на y. И тогда средний риск будет

. (2)

Воспользуемся формулой Байеса и тогда

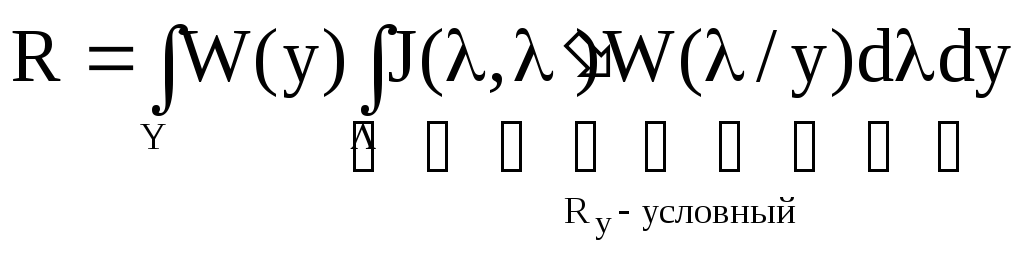. (3)

Внутренний интеграл получил название условного среднего риска.

Критерий минимального среднего риска означает, что приемник должен выносить оценки ` таким образом, чтобы средний риск был минимален.

Чтобы минимизировать средний риск, нужно минимизировать условный средний риск:

. (4)

Минимум среднего риска иными словами требует минимум функции потерь. Рассмотрим работу критерия на конкретных примерах. Известно, что сообщения могут быть непрерывные и дискретные. Предположим, канал связи предназначен для передачи непрерывных сообщений. Для оценки качества такого канала представляет интерес величина отклонения принятого сообщения от переданного. Поэтому введем следующую функцию потерь: . Поскольку  и ’, запишем условный риск,

(5)

и найдем то значение ’ при котором удовлетворяется его минимум. Известным путем исследуем функцию Rу на экстремум:

,

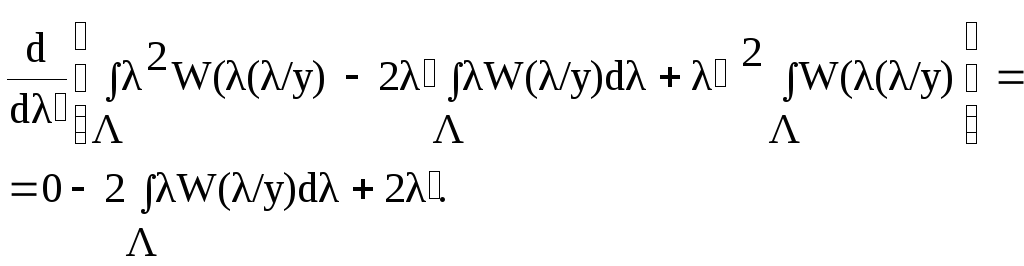(6)

Из последнего выражения следует , то есть принимаемое сообщение должно быть равно математическому ожиданию переданного сообщения m_λ при условии приема у. Такой вывод находится в полном соответствии со здравым смыслом.

Далее рассмотрим дискретный канал связи в котором передаются дискретные сообщения (слова, цифры и т. д.). В выражении среднего риска (2) следует интегрирование заменить суммированием, так как мы имеем дело с конечным множеством сообщений. Тогда

. (7)

зададим функцию потерь в следующем виде: , где

.

Тогда средний риск будет

. (8)

Если потребовать его минимума, то это означает, что система должна обеспечить минимальной вероятности ошибки, R_min=min p_ош.

В основу критерия минимального среднего риска положен условный закон распределения W(λ/y), который называется апостериорное распределение вероятности (АПРВ). Это условный закон распределения передаваемого сообщения при приеме у(t). Эту функцию должен вычислять приемник, получив сигнал у(t). Задача эта должна выполняться устройством оптимальной обработки (рис. 6)

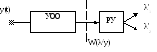
Рис. 6. Вычисление АПРВ.

При этом есть некоторые сложности. Принимая сигнал в вольтах, УОО должно вычислить по нему функцию совершенно другого аргумента . Рассмотрим АПРВ и постараемся определить ее через другие функции. Согласно формуле Байеса

или

. (9)

В это выражение входят два безусловных статистических закона: W()- передаваемого сообщения и W(y)-закон принимаемого сигнала. Задача приема сигналов особенно интересна тогда, когда система связи работает в наиболее тяжелых условиях, то есть передает наибольшее количество информации. Следовательно, мы должны рассмотреть такой источник, который производит максимальное количество информации, в теории информации доказано что его статистический закон будет равномерным и

, (10)

где ₁ и ₂ – граничные значения сообщения.

Второй безусловный закон W(y) – это голая статистика сигнала входе. В приемнике решающее устройство (см. рис. 6) по вычисленной АПРВ должно произвести выбор в пользу того или иного сигнала. Очевидно, что на это никак не повлияет данный статистический закон, так он одинаков для всего множество сигналов. Таким образом и

(11)

Условный статистический закон W(y/λ) называется функция правдоподобия. Он подлежит вычислению вместо функции АПРВ и имеет своим аргументом входной сигнал y(t). Этот закон имеет наиважнейшее значение в критериях оптимального приема.

Критерий максимальной функции правдоподобия.

Один из примеров применения функции правдоподобия это одноименный критерий. Приемник, принимая сигнал y(t), должен выносить решение в пользу того переданного сообщения _i (сигнала S_i), для которого функция правдоподобия максимальна. Это положение иллюстрируется на рис. 7. Таким образом приемник должен вычислить функцию правдоподобия или ее какие то показатели (обратите на это внимание!), произвести сравнение их и сделать выбор. Данный критерий позволит определить оптимальный порог приемника.

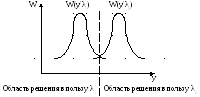
Рис. 7. Критерий максимальной функции правдоподобия.

Нахождение функции правдоподобия.

Допустим, передаваемый сигнал за время его существования представлен детерминированной величиной S(t,). Помимо его на входе приемника присутствует помеха n(t), которая всегда случайна. Таким образом принимаемый сигнал представляется суммой , .

На рис.8 показан вид временной функции помехи с нулевым средним значением, m_n=0. Можно ввести для нее статистический закон W_п(n).

Рис. 8. Временная функция помехи

Очевидно, что если к помехе прибавить простейший сигнал, например, постоянное напряжение, то течение функции во времени не изменится. Произойдет только ее смещение по оси напряжения (рис.9) на величину сигнала .

Рис.9. Сигнал и помеха.

Теперь обратимся к закону распределения y(t). Очевидно, что он будет такой же как и у помехи , но только с ненулевым математическим ожиданием, которое будет равно сигналу . Поэтому

. (12)

Сформулируем правило. Функция правдоподобия будет иметь тот же вид что и статистический закон распределения помехи, в который вводится математическое ожидание равное сигналу.

Предположим, что в приемнике идет цифровая обработка сигнала. Это значит, что принимаемый сигнал представляется множеством отсчетов (выборкой) рис.10.

y(t)

t

Δt

t₁ 2t₁ 3t₁

Рис. 10 Дискретизация принимаемого сигнала.

В момент времени t_h имеем y_h=S_h+n_h. Пользуясь предыдущим выводом, запишем выражение функции правдоподобия при одном отсчете:

. Обозначим H – количество отсчетов в сигнале.

Будем считать что все отсчеты статистически независимы и полная функция правдоподобия для всего сигнала будет:

. (13)

Дальнейшая конкретизация функции правдоподобия может быть проведена только при задании вида статистического закона помехи. Согласно критерию максимальной функции правдоподобия, приемник должен анализировать эти функции правдоподобия и выбирать максимальную. Допустим на приемник воздействует помеха типа «белый шум» с конечной мощностью, Гауссовским законом распределения. Искажения сигнала в приемнике отсутствуют. Найдем функция правдоподобия. Статистический закон помехи при нулевом математическом ожидании будет

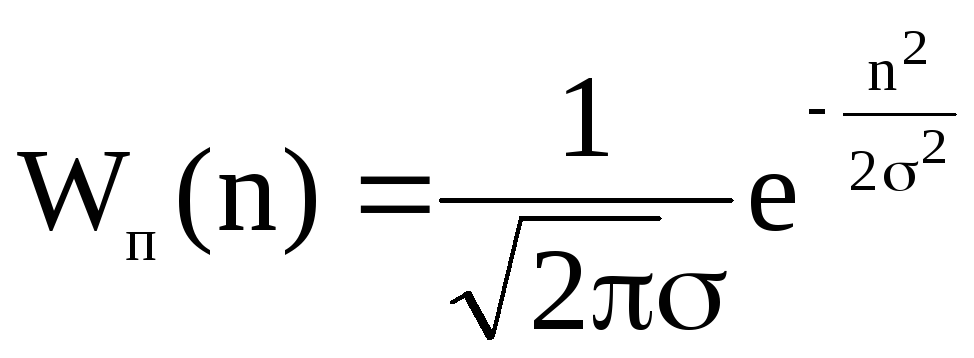, (14)

где  - среднеквадратичное отклонение.

При представлении входного сигнала выборкой имеем закон для одной выборки

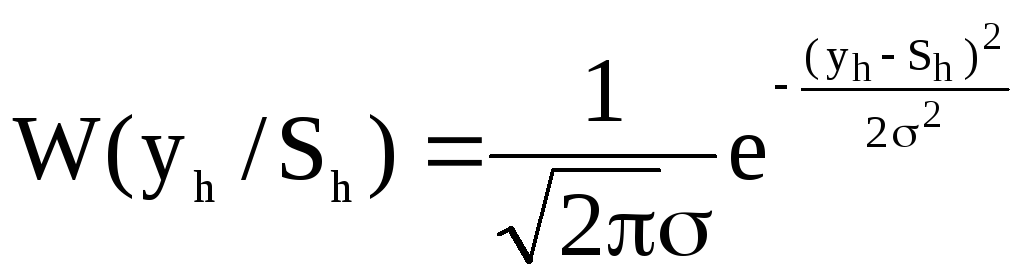, (15)

и для всего сигнала

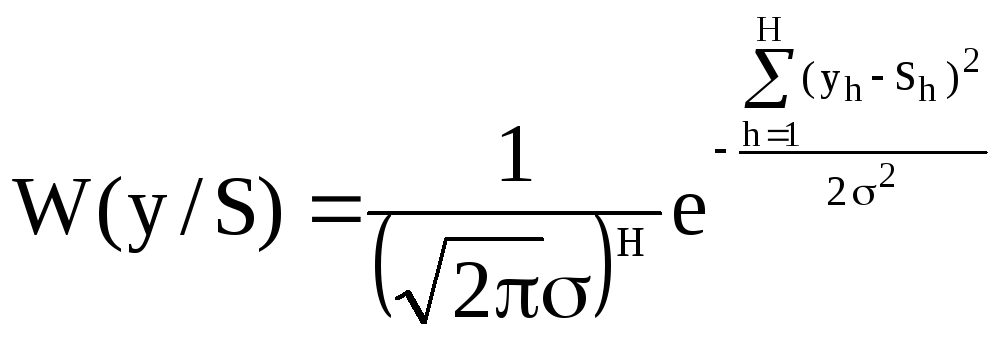. (16)

Ранее неоднократно было замечено, что приемник производит выбор «что больше?», W(y/S_i) или W(y/S_j), то есть необходимо сравнить функции правдоподобия или их показатели степеней.

Множитель – одинаковая для всех функций правдоподобия и в сравнении может не участвовать. Остаются для сравнения экспоненты, но вместо них можно сравнить показатели; какой из них меньше, та функция правдоподобия и будет больше. Или чем меньше выражение

, (17)

тем экспонента больше. Множитель 1/2² исключим из сравнения так как он одинаков для всех сигналов. По этой же причине можно исключить из (17) первую сумму . Таким образом

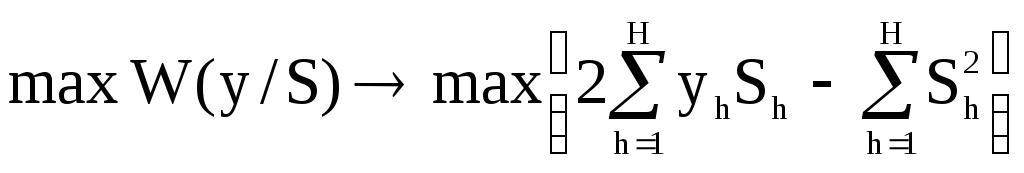. (18)

Рассмотрим содержание (18). Первая сумма означает усреднение во времени произведения двух сигналов, обладающих свойством эргодичности. По смыслу есть взаимная корреляция двух сигналов, принятого и опорного, или их скалярное произведение. Вторая сумма – энергия передаваемого сигнала. Таким образом

. (19)

Полученное выражение дает возможность построить оптимальный приемник, работающий по критерию максимальной функции правдоподобия. Рассмотрим это на примере бинарной системы связи.

Допустим, что передаются два сигнала (два сообщения) S₁ и S₂. Приемник должен вычислять для каждого из передаваемых сигналов , сравнить результаты и найти максимальный результат и принять решение в пользу сигнала, для которого получен максимум. Несложно построить функциональную схему такого приемника, рис. 11.

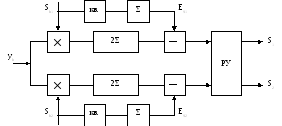
Рис. 11. Схема оптимального приемника.

Решающее устройство, РУ, может быть реализовано несложной схемой на транзисторах, рис. 12.

S₂

S₁

U₂

U₁

VT1

VT2

Рис.12. Решающее устройство

Большее напряжение U_i открывает соответствующий транзистор и он своим эмиттерным током закрывает второй транзистор. На коллекторе открытого формируется низкое напряжение, свидетельствующее о большим напряжении U_i. Схема приемника зависит от вида передаваемых сигналов и в некоторых случаях может быть упрощена. Например, для сигналов с активной паузой, это сигналы частотной и фазовой модуляции их энергии равны E_S1=E_S2 и данные параметры могут быть исключены из сравнения. Сравнению подлежат только взаимные корреляции принимаемого сигнала и передаваемых. Структура приемника для этого случая показана на рис. 13.

Рис. 13. Схема оптимального приемника.

Критерий максимальной функции правдоподобия не единственный; существуют и другие предпосылки для решения задачи приема. Рассмотрим их в следующей лекции.