
3443 Курсовая Работа ЭЭ
.pdf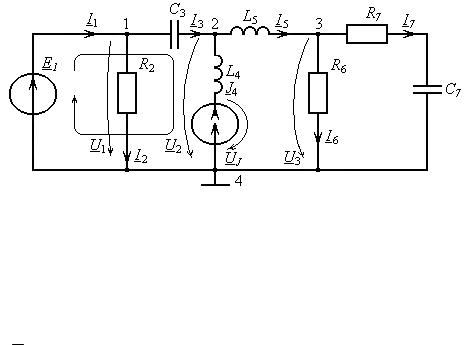
Рис. 10. Схема для определения напряжения на источнике тока
С учетом этого определим комплексную мощность идеального источника тока:
*
S J = U J J 4 = 248,222e j0,0608 2,06e j0,7 = 590,695e j0,684 = 370,338 + j352,583 .
Активная и реактивная мощности, развиваемые источниками, равны соответственно:
Pист. = Re(SE1) + Re(SJ4) = 87,338 + 370,338 = 457,676 Вт,
Qист. = Im(SE1) + Im(SJ4) = 20,85 + 352,583 = 373,474 ВАр.
Определим погрешность расчета δ по следующим формулам:
δ P % = |
|
Pист. − Pпот. |
|
2 |
100% , |
|
δQ % = |
|
Qист. − Qпот. |
|
2 |
100% . |
(38) |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Pист. + Pпот. |
|
|
|
Qист. + Qпот. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
δ P % = |
|
|
457,676 − 457,688 |
|
|
|
2 |
100% = 2,6 10−3% , |
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
457,676 + 457,688 |
|
|
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
δQ % = |
|
373,474 − 373,415 |
|
|
|
2 |
100% = 5,07 10−3% . |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
373,474 + 373,415 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Как видно из приведенных результатов расчета, баланс активной и реактивной мощностей выполняется. Расхождение в расчете не превышает сотую долю процента. Из этого можно сделать вывод о том, что расчет токов выполнен верно.
9. Определим ток I3, используя теорему об эквивалентном источнике напряжения. При этом вся схема превращается в схему, показанную на рис. 11. Для этой схемы ток I3 можно рассчитать по формуле:
I 3 = |
EЭ |
, |
(39) |
|
Z Э + Z 3 |
||||
|
|
|
||
|
21 |
|
|
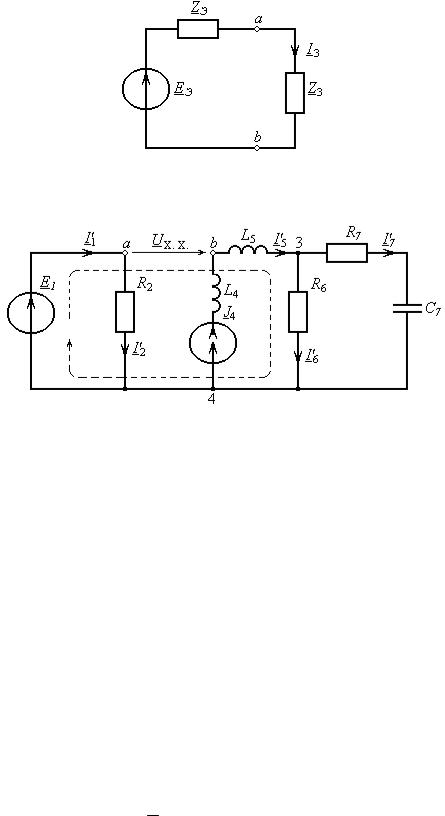
где EЭ = UX. X., а UX. X – напряжение холостого хода на разомкнутых зажимах между узлами a и b, как это показано на рис. 12.
Рис. 11. Схема для расчета тока I3 с использованием теоремы об ЭИН
Рис. 12. Схема для расчета UХ. Х.
Для расчета UХ. Х. размыкаем ветвь с емкостью С3 и находим напряжение между точками разрыва. Обозначим токи в ветвях схемы. Так как схема изменилась, то токи в ветвях схемы тоже изменятся и будут другие. Пометим их штрихом. Напряжение UХ. Х. найдем из уравнения, записанного по второму закону Кирхгофа для контура, направление обхода которого на схеме показано пунктирной линией. В этом случае требуется рассчитать только ток I6′. Этот ток можно найти из формулы делителя токов.
I 6 ' = J 4 |
|
|
R7 |
+ Z C 7 |
= 2,06e |
− j 0,7 |
108 − j46,3 |
|
= 0,742 |
− j0,898 = 1,165e |
− j 0,88 |
. |
|
R6 |
+ R7 + Z C 7 |
|
94,5 + 108 − |
j46,3 |
|
||||||||
|
|
|
|
|
|
|
|
||||||
В этом случае уравнение по второму закону Кирхгофа будет иметь следующий вид:
+ J 4 Z L5. + I 6 'R6 = E1 ,
откуда
|
U |
X.X. = E1 − J 4 Z L5. − I 6 'R6 . |
(40) |
|
Подставим в это выражение числовые значения:
22
π
U Х. Х. = 91,6 + j33,3 − 2,06e− j 0,7 81e j 2 − 1,165e j 0,88 94,5 =
= 91,6 + j33,3 − 107,494 − j127,622 − 70,144 + j84,89 = 86,05 − j9,3 = 86,551e− j 3,034 , B.
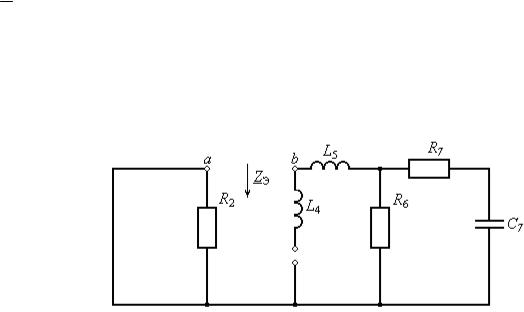
Для определения ZЭ в схеме рис. 12 параметры источников приравниваем к нулю и получаем схему рис. 13.
Рис. 13. Схема для определения ZЭ
Внутреннее сопротивление эквивалентного источника определим как сопротивление относительно точек a и b в схеме рис. 13.
|
R Z |
7 |
|
94,5 117,5e− j0,405 |
= 52,6 + j71,418 = 88,692e j0,936 |
|
Z Э = Z L5 + |
6 |
= j81+ |
|
|||
R6 + Z 7 |
94,5 + 108 − j46,3 |
|||||
|
|
|
||||
Теперь, зная EЭ и ZЭ, рассчитаем ток I3.
I 3 = |
86,551e− j3,034 |
= |
86,551e− j3,034 |
= 1,527e− j2,651 = −1,347 − j0,719 |
|
52,6 + j71,418 − j92,6 |
56,7e− j0,383 |
||||
|
|
|
Ом. (41)
А. (42)
Из сравнения полученного результата со значением тока I3, найденного в п. 7, следует, что и по модулю, и по аргументу эти значения совпадают.
10. Построим векторные диаграммы токов и напряжений для узла 3 и третьего контура схемы, состоящего из сопротивлений Z6 и Z7, в схеме, приведенной на рис. 8.
По первому закону Кирхгофа для узла 3:
I5 = I6 + I7 |
; 0,229 − j2,046 = −0,08 − j1,162 + 0,309 − j0,884 . |
(43) |
Для третьего контура по второму закону Кирхгофа: |
|
|
I 7 |
R7 + I 7 Z C7 − I 6 R6 = 0 . |
(44) |
После подстановки числовых значений получим:
0,937e− j1,235 108 + 0,937e− j1,235 46,3e− j1,571 − 1,165e− j1,64 94,5 = 0 .
23
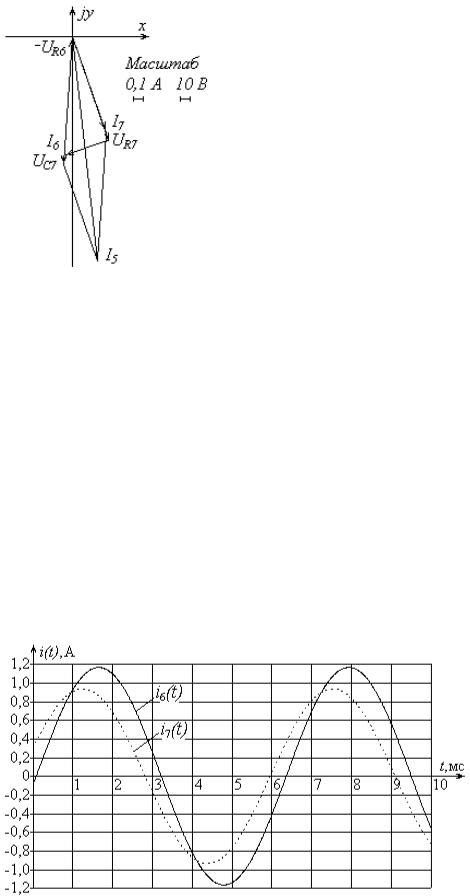
Выбрав масштаб по току и напряжению, строим векторные диаграммы, которые приведены на рис. 14.
Рис. 14. Векторные диаграммы токов и напряжений
Для сравнения построим временные зависимости токов и напряжений, показанных на векторной диаграмме. Временные зависимости для токов i5(t), i6(t) и i7(t) имеют следующие выражения:
i5 (t) = 2,912 cos(1000t − 0,70) А, i6 (t) = 1,647 cos(1000t − 1,64) А, i7 (t) = 1,325 cos(1000t − 1,235) А.
Наибольший интерес представляют токи i6(t) и i7(t), графики временных зависимостей для этих токов приведены на рис. 15.
Рис. 15. Графики временных зависимостей для токов i6(t) и i7(t)
24
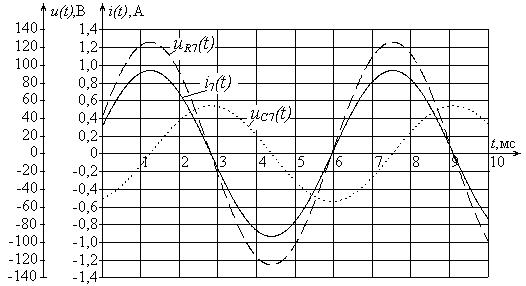
Запишем временные зависимости для напряжений uR6(t), uR7(t) и uC7(t).
uR6 (t) = 110,07 cos(1000t − 1,64) В, uR7 (t) = 125,8 cos(1000t − 1,64) В, uC7 (t) = 53,9 cos(1000t − 2,805) В.
Графики временных зависимостей для тока i7(t) и напряжений uR7(t) и uC7(t) приведены на рис. 16.
Рис. 16. Графики временных зависимостей тока i7(t) и напряжений uR7(t) и uC7(t)
По этим графикам можно определить фазовый сдвиг между токами и напряжениями. Так, из первого графика видно, что ток i7(t) опережает ток i6(t). Величина фазового сдвига равна 0,4 мс. Умножив это значение на частоту ω = 1000 рад/с, получим значение фазового сдвига 0,4 рад. Данное значение совпадает со значением, полученным из формул, приведенных в табл. 1.
Из второго графика видно, что напряжение на резисторе совпадает по фазе с током, а напряжение на емкости отстает от тока на π/2.
Пример 2. Расчет цепи с независимыми источниками.
1.Задан код схемы 9. 3. 13. 10. 4. 5. 3. Схема, составленная в соответствии с этим кодом, приведена на рис. 17.
2.По формулам, приведенным в задании, рассчитаем величины элементов схемы и параметры источников.
R1 = 10,5 Ом; R2 = 15,75 Ом; R3 = 21 Ом; R7 = 42 Ом; L4 = 26,25 10-3 Гн;
L5 = 31,5 10-3 Гн; C3 = 42 10-6 Ф; C6 = 73,5 10-6 Ф.
i1 (t) = 2,2 Cos(1000t − 0,175) А; i4 (t) = 2,5Cos(1000t − 0,70) А.
25
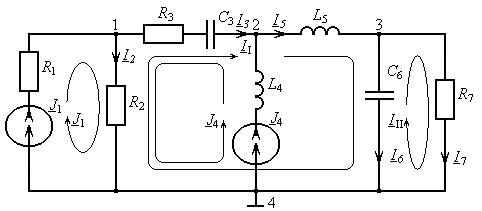
Рис. 17. Схема для расчета к примеру 2
3. Представим гармонические функции i1(t) и i4(t) в виде комплексных действующих значений и запишем их в показательной и алгебраической формах записи.
J1 = 1,556 e− j0,175 = 1,532 − j0,271, А,
J 4 = 1,767767 e− j0,70 = 1,352 − j1,139 , А.
4. Определим комплексные сопротивления реактивных элементов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
Z |
L4 |
= jωL |
= jX |
L4 |
= j103 26,25 10−3 |
= j26,25 = 26,25e j 2 |
Ом; |
|
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
Z |
L5 |
= jωL |
= jX |
L5 |
= j103 31,5 10−3 = j31,5 = 31,5e j 2 Ом; |
|
|
|
|
||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Z |
|
= |
1 |
|
|
= − jX |
|
= − j |
1 |
|
= − j23,8095238 = |
23,8095238e |
− j |
π |
Ом; |
||||
C3 |
|
|
|
C3 |
|
|
|
|
|
2 |
|||||||||
jωC |
|
103 42 10− |
6 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
− j |
π |
||
Z |
C6 |
= |
|
|
|
= − jX |
C6 |
= − j |
|
|
|
|
= − j13,6054422 = 13,6054422e |
|
|
2 Ом. |
|||
jωC |
|
|
103 73,5 10−6 |
|
|
||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Седьмая ветвь схемы содержит сопротивление R7 и емкость C7. Определим их комплексное сопротивление Z7 и комплексную проводимость Y7:
Z |
7 |
= R |
+ |
1 |
= R |
− jX |
C 7 |
= 108 − j46,3 = 117,506e− j0,405 |
Ом. |
|
||||
|
|
|
||||||||||||
|
|
7 |
|
jωC7 |
7 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Y 7 |
= |
1 |
= |
|
|
1 |
|
= 8,51 10−3e j0,405 = 7,822 10−3 + j3,35310−3 |
См. |
|||||
Z 7 |
117,5e− j0,405 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
6. Определим число уравнений, которое надо составить для расчета токов в ветвях схемы методом контурных токов и методом узловых напряжений. Предварительно проведем топологический анализ схемы. Для чего определим число узлов в схеме NУ, число ветвей NВ, число идеальных источников тока NJ и число особых ветвей схемы NОС.
NУ = 4; NВ = 7; NJ = 2; NОС = 0.
NМКТ = NВ – NУ+1 – NJ = 7 – 4 +1 – 2 = 2;
NМУН = NУ – 1 – NОС = 4 – 1 – 0 = 3.
26
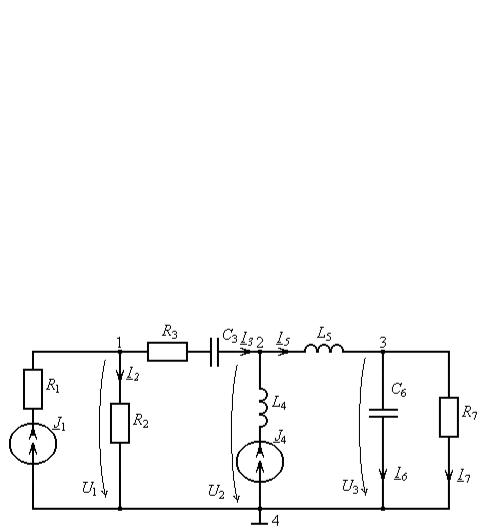
Составим системы уравнений тем и другим методом и выразим токи в ветвях через контурные токи и узловые напряжения.
Для составления системы уравнений по МКТ выберем три основных контура с контурными токами II, III, IIII и два дополнительных контура с контурными токами J1 и J4, равными токам источников (рис. 17). Система уравнений в этом случае будет иметь следующий вид:
I I (R2 + R3 + Z C3 + Z L5 + Z C 6 )− J1R2 − J 4 (R2 + R3 + Z C3 )− I II Z C6 |
= 0 |
(45) |
I II (Z C6 + R7 )− I I Z C6 = 0 |
. |
|
|
|
Определив из полученной системы уравнений неизвестные контурные токи, выразим через них токи в ветвях схемы:
I2 = J1 – II + J4; I3 = II – J4; I5 = II; I6 = II – III; I7 = III.
Для расчета токов по МУН воспользуемся схемой рис. 18. В схеме рис. 18 показан базисный узел, для которого напряжение равно нулю, т. е. U4 = 0. Покажем узловые напряжения U1, U2, U3. В этом случае система уравнений, составленная по МУН, будет иметь следующий вид:
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
U |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
− U |
|
|
|
|
|
|
|
|
|
|
|
|
|
= J |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
R |
|
|
|
|
R |
|
+ Z |
|
|
|
|
|
|
|
|
2 |
|
|
R |
|
+ Z |
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
C3 |
|
|
|
|
|
|
|
3 |
|
|
|
C3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|||||||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− U |
|
|
|
|
|
|
|
|
|
|
|
|
− U |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
R |
|
+ Z |
C3 |
Z |
L5 |
|
|
|
|
|
|
1 R |
|
+ Z |
C3 |
|
|
|
|
3 |
|
Z |
L5 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
− U |
|
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
3 |
|
|
Z |
L5 |
|
|
Z |
C6 |
|
|
R |
|
|
|
|
|
|
|
|
2 |
Z |
L5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= J 4 |
. |
(46) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18. Схема для расчета по МУН
Решив систему уравнений, найдем неизвестные узловые напряжения U1, U2, и U3 и выразим токи в ветвях схемы через узловые напряжения:
I 2 |
= |
|
U |
1 |
; I 3 = |
U1 − U 2 |
; I 5 |
= |
|
U |
2 − |
U |
3 |
; I 3 |
= |
|
U |
1 − |
U |
2 |
; I 6 = |
U 3 |
; I 7 |
= |
|
U |
3 |
; I1 = I 2 + I 3 . (47) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
R3 + Z C3 |
|
|
|
|
|
|
|
|
|
|
Z C6 |
|
|
|
|||||||||||
|
|
|
R2 |
|
|
|
|
Z L5 |
|
|
|
Z C3 |
|
|
|
R7 |
||||||||||||
27
7. Рациональным методом, т. е. методом, требующим решения системы с меньшим числом уравнений, является в данном случае МКТ. Выполним расчет токов в ветвях схемы рис. 17 данным методом. Для этого запишем систему уравнений по МКТ в каноническом виде и подставим в нее числовые значения.
I I (15,75 + 21− j23,8095238 + j31,5 − j13,6054422)+ I II ( j13,6054422) = |
|
|
= 1,5556349e− j0,17515,750 + 1,767767e− j0,7 (15,75 + 21− j23,8095238) |
. |
(48) |
I I ( j13,6054422)+ I II (− j13,6054422 + 42) = 0 |
|
|
|
|
|
Решим данную систему уравнений методом Крамера. Для этого вычислим главный определитель системы Z и два дополнительных 1 и 2.
Z = |
|
|
|
36,75 − j5,915 |
j13,605 |
|
= 1,648103 − j748,429 = 1,810 103 e− j0,426 |
, |
|||||
|
|
||||||||||||
|
|
|
|
|
j13,605 |
42 − j13,605 |
|
|
|
|
|
||
1 = |
|
46,700 − j78,31 |
j13,605 |
|
|
|
== 895,980 − j3,924 103 = 4,025 103 e− j1,346 |
, |
|||||
|
|
|
|||||||||||
|
|
0 |
42 − j13,605 |
|
|
|
|
|
|
|
|||
2 = |
|
|
36,75 − j5,915 |
46,700 − j78,31 |
|
= 1,065 103 − j635,38 = 1,241 103 e− j2,604 . |
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
− j13,605 |
0 |
|
|
|
|
|
|
|
Определим контурные токи II, и III.
I I = |
1 |
= 1,347 − j1,769 = 2,224e− j0,92 А, |
I II = |
2 |
= −0,391− j0,563 = 0,685e− j2,178 А. |
|
Z |
Z |
|||||
|
|
|
|
Выразим токи в ветвях схемы через контурные токи:
I2 = J1 – II + J4; I3 = II – J4; I5 = II; I6 = II – III; I7 = III.
Вычислим токи в ветвях схемы:
I2 = 1,532 – j0,271 – 1,347 + j1,769 + 1,352 – j1,139 = 1,537 + j0,36 = 1,578ej0,23 А, I3 = 1,347 – j1,769 – 1,352+j1,139 = –4,9 10–3 –j0,631 = 0,631ej1,579 А,
I5 = 1,347 – j1,769 = 2,22ej0,92 А,
I6 = 1,347 – j1,769 + 0,391+j0,563 = 1,738 – j1,206 = 2,116ej0,607 А, I7 = – 0,391 – j0,563 = 0,685e–j2,178 А,
J1 = 1,5556349 e− j0,175 = 1,531875 − j0,2708487 А, J 4 = 1,767767 e− j0,70 = 1,3520627 − j1,138826 А.
28
Результаты расчетов сведем в табл. 2.
|
|
|
|
Таблица 2 |
Рассчитанный |
Алгебраическая |
Показательная |
Мгновенные значения |
|
ток |
форма записи |
форма записи |
рассчитанных токов, А |
|
|
|
|
|
|
J |
1 |
1,532 – j0,271 |
1,556e–j0,175 |
i (t) = 2,2 cos(1000t − 0,175) |
|
|
|
1 |
|
I |
2 |
1,537 + j0,36 |
1,578ej0,23 |
i (t)= 2,232 cos(1000t + 0,23) |
|
|
|
2 |
|
I3 |
–4,9 10–3 –j0,631 |
0,631ej1,579 |
i3 (t) = 0,892 cos(1000t − 1,579) |
|
J |
4 |
1,352 – j1,139 |
1,768e–j0,7 |
i (t) = 2,5cos(1000 t − 0,70) |
|
|
|
4 |
|
I5 |
1,347 – j1,769 |
2,22e–j0,92 |
i5 (t) = 3,145cos(1000t − 0,92) |
|
I6 |
1,738 – j1,206 |
2,116e–j0,607 |
i6 (t) = 2,992cos(1000t − 0,607) |
|
I7 |
– 0,391 – j0,563 |
0,685e–j2,178 |
i7 (t) = 0,969cos(1000t − 2,179) |
|
8. Проверим правильность расчета, составив и рассчитав баланс активной и реактивной мощностей.
Активная потребляемая мощность:
Pпотр. = R1J12 + R2I22 + R3I32 + R7I72 = 10,5 1,5562 + 15,75 1,5782 + 21 0,6312 + +42 0,6852 = = 25,41 + 39,236 + 8,35 + 19,726 = 92,722 Вт.
Реактивная потребляемая мощность:
Qпотр. = – XC3 I32 + XL4 J42 + XL5 I52 – XC7 I72 = – 23,81 0,6312 + 26,25 1,7682 + 31,5 2,222 – –13,605 0,6852 = – 9,467 + 82,03 + 155,78 – 60,895 = 167,45 ВАр.
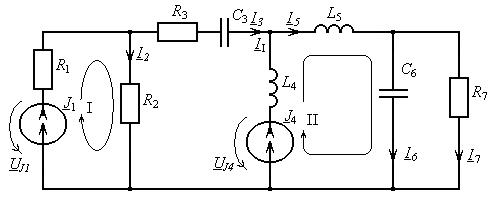
Определимкомплекснуюмощность, развиваемуюидеальнымиисточникамитокаJ1 иJ4. Для определения комплексной мощности идеального источника тока надо найти напряжение на его зажимах. С этой целью запишем уравнение по второму закону Кирхгофа для контуров, указанных на рис. 19. В первый контур войдут ветви Z1 и Z2, а во второй
ветви Z4, Z5 и Z6.
Рис. 19. Схема для определения напряжения на источниках тока
29
U |
J 1 |
= J |
1 |
R + I |
2 |
R |
|
= 1,556e− j 0,175 |
10,5 + 1,578e j 0,23 |
15,75 = 16,085 − j2,844 + 24,205 + j5,665 = |
|
|
|
|
1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|||||
= 40,290 + j2,821 = 40,388e j 0,07 B. |
|
|
|||||||||
|
U |
J 4 = J 4 Z L4 + I 5 Z L5 + I 6 Z C6 = 1,768e− j0,7 |
j26,25 + 2,22e− j0,92 j31,5 + 2,116e− j0,607 (− j13,605) = |
|
|||
|
= 29,894 + j35,492 + 55,735 + j42,434 − 16,414 |
− j23,645 = 69,216 + j54,281 = 87,962e j0,665 B. |
|
С учетом рассчитанных значений напряжений на источниках тока определим комплексную мощность идеальных источников тока:
* |
|
|
|
* |
= 40,388e j0,07 1,556e j0,175 + 87,962e j0,665 1,768e j0,7 = 62,829e j0,245 + |
||
Sист. = |
U |
J1 J1 |
+ |
U |
J 4 |
J 4 |
|
|
|
||||||
+ 155,496e j1,365 = 60,954 + j15,234 + 31,768 + j152,216 = 92,722 + j167,45.
Активная и реактивная мощности, развиваемые источниками, равны соответственно:
Pист. = Re(SJ1) + Re(SJ4) = 92,722 Вт,
Qист. = Jm(SJ1) + Jm(SJ4) = 167,45 ВАр.
Определим погрешность расчета δ по формулам (49):
δ P % = |
|
|
Pист. − Pпот. |
|
2 |
100% , δQ % = |
|
Qист. − Qпот. |
|
2 |
100% . |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Pист. + Pпот. |
|
|
|
Qист. + Qпот. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
δP % = |
|
|
92,722 − 92,722 |
|
|
|
2 |
100% = 0% , |
(49) |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
92,722 + 92,722 |
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
δQ % = |
|
|
167,45 − 167,45 |
|
2 |
100% = 0% . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
167,45 + 167,45 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Как видно из приведенных результатов расчета, баланс активной и реактивной мощностей выполняется. Расхождение в расчете равно нулю. Из этого можно сделать вывод о том, что расчет токов выполнен верно.
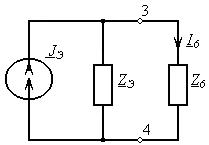
9. Определим ток I6, используя теорему об эквивалентном источнике тока. При этом вся схема превращается в схему, показанную на рис. 20.
Рис. 20. Схема с эквивалентным источником тока
Для этой схемы ток I6 можно рассчитать по формуле (50):
I 6 = J Э |
Z Э |
. |
(50) |
|
Z Э + Z 6 |
||||
|
|
|
30
