
МУ для подготовки к АКР 1 семестр выс. мат
..pdf
Argz = аrgz + 2πk, где |
аrgz – |
главное значение аргумента, заключенное в |
|
промежутке (– π; π], |
то есть |
arg z |
(иногда в качестве главного |
значения аргумента берут величину, принадлежащую промежутку [0; 2π)).
Аргумент φ определяется из формулы tg |
y |
. Так как |
arg z |
, то |
|
x |
|||||
|
|
|
|
||
получаем, что |
|
|
|
|
arctg xy arg z = arctg xy 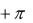 arctg xy
arctg xy 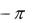
для внутренних точек I, IV четвертей,
для внутренних точек II четверти,
для внутренних точек III четверти.
Тогда модуль комплексного числа z = – 4 
 3 – 4∙i:
3 – 4∙i:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = x2 |
y2 = ( 4 3)2 ( 4)2 = 48 16 = 64 = 8, |
|||||||||||||||||||||||||||||||||||||||
а так как точка М находится в III четверти, то аргумент |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
arctg |
у |
|
|
|
|
|
arctg |
|
|
|
4 |
|
|
|
|
|
arctg |
|
1 |
|
|
|
|
|
|
5 |
. |
|||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||
Тогда |
z 8 |
cos |
5 |
|
|
|
i sin |
5 |
|
|
– тригонометрическая форма |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
6 |
|
|
6 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
комплексного числа z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3) Для нахождения п z |
|
|
воспользуемся формулой |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
2 k |
), где k = 0, 1, 2, …, п – 1. |
||||||||||||||||||||||||||
wk = n z |
= n r (cos |
|
|
+ isin |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В нашем случае имеем п = 3 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
2 k |
|
|
|
5 |
2 k |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
wk = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 3 |
|
4 i |
= 3 8 (cos |
|
|
|
|
|
+ isin |
|
|
|
), где k = 0, 1, 2. |
||||||||||||||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Придавая k последовательно значения 0, 1, 2, находим все три значения корней:
w0 |
= 3 |
|
(cos( |
5 |
|
) + isin( |
5 |
)) ≈ 2∙(0,643 – 0,766i) = 1,286 – 1,532i, |
|||||||||||||||||
8 |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
18 |
18 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
w1 |
= 3 |
|
(cos |
7 |
|
|
+ isin |
7 |
|
) ≈ 2∙( 0,342 + 0,94i) = 0,684 + 1,88i, |
|||||||||||||||
8 |
|
|
|
||||||||||||||||||||||
18 |
|
|
18 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
|
|
19 |
|
|
|
|
|
19 |
|
|
3 |
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
w2 |
= |
|
(cos 18 |
+ isin |
|
|
18 ) = |
|
(– cos18 – isin18 ) ≈ 2∙(– 0,985 – |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
0,174i) =
= – 1,97 – 0,348i.
31

Тема 6. Первообразная и неопределенный интеграл, определенный интеграл
1 Знать определение первообразной и неопределенного интеграла.
2 Знать и применять основные свойства неопределенного интеграла.
3 Применять таблицу неопределенных интегралов.
4 Проверять результаты интегрирования дифференцированием.
5 Применять формулу замены переменной в неопределенном интеграле.
6 Применять формулу интегрирования по частям для неопределенного интеграла.
7 Знать определение определенного интеграла.
8 Применять формулу Ньютона-Лейбница для вычисления определенных интегралов.
9 Знать и применять основные свойства определенного интеграла.
10 Применять формулу замены переменной в определенном интеграле.
11 Применять формулу интегрирования по частям для определенного интеграла.
12 Вычислять площадь простейших геометрических фигур с помощью определенного интеграла.
13 Применять понятие определенного интеграла для вычисления длин дуг плоских кривых, заданных параметрическими уравнениями и уравнениями в полярной системе координат.
Задачи для самостоятельного решения
1 |
Если F(x) – одна из первообразных функции f(x),то |
f (x)dx = … |
||||||||||||||||
2 |
Производная от интеграла |
f (x)dx |
равна … |
|
||||||||||||||
3 |
Дифференциал от интеграла d |
|
f (x)dx равен … |
|
||||||||||||||
4 |
Интеграл |
dF(x) равен … |
|
|
|
|
|
|
|
|||||||||
5 |
Если f (x)dx F(x) C , то |
|
f (ax |
b)dx … |
|
|||||||||||||
6 |
Если функция |
F (x) |
|
1 |
arctg |
x |
|
первообразная |
функции f (x) , то |
|||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
||
функция f(x) равна … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7 |
Если f (x) |
|
|
|
1 |
|
|
, то ее первообразная F (x) равна … |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
a 2 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
||
8 |
Найти интеграл |
|
(3x 2 |
2x |
5)dx . |
|
|
|||||||||||
9 |
Найти интеграл |
|
2x3 |
4x |
6 |
dx . |
|
|
||||||||||
|
|
|
|
x 4 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 3sin(2x 1)dx |
|
k cos(2x |
1) C . Тогда k = … |
|
||||||||||||||
11 2e5x 3dx |
|
ke5x |
3 C . Тогда k = … |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
||
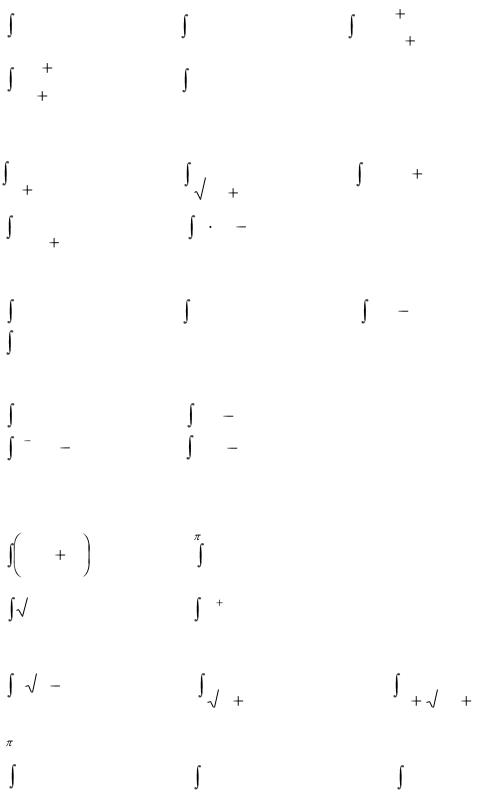
12 Найдите интегралы: |
|
|
|
|
|
|||||
а) |
cos x d (cos x) ; |
б) |
tg2 x d (tgx) ; |
в) |
d (1 |
ln x) |
; |
|||
sin 2 (1 |
|
|||||||||
|
|
|
|
|
|
|
|
ln x) |
||
г) |
|
d (1 |
x2 ) |
; |
д) |
earcsin x d (arcsin x) . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
x2 |
|
|
|
|
|
|
||
13 Какую из подстановок целесообразно использовать для замены переменной в интеграле:
а) |
|
e x |
|
dx ; |
б) |
|
x |
2 |
|
dx ; |
в) x(2x2 1)5 dx ; |
|
3 4e x |
|
|
|
|
|
|||||||
|
x3 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|||||
г) |
|
x |
|
|
dx ; |
д) x (x 2)7 dx . |
|
|||||
|
|
|
|
|
||||||||
|
2x 2 |
5 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
14 Какое из выражений целесообразно принять за U при интегрировании по частям интеграла:
а) x2e3x dx ; |
б) x ln xdx; |
в) (2x 3) cos xdx ; |
г) xarctgxdx .
15 Какое из выражений целесообразно принять за dV при интегрировании по частям интеграла:
а) |
xarctgxdx ; |
б) |
(3x |
2) cos5xdx ; |
в) |
e x (x 1)dx ; |
г) |
ln( x |
5)dx . |
16 Если F(x) является первообразной функции f(x), то справедлива формула Ньютона-Лейбница …
17 Вычислить определенные интегралы:
|
2 |
|
|
2 |
|
|
|
|
а) |
2x2 |
dx; |
б) |
cos xdx ; |
||||
x |
||||||||
|
1 |
|
|
|
|
0 |
||
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
1 |
|
в) |
|
xdx ; |
|
|
г) |
еx 1dx . |
||
|
1 |
|
|
|
|
|
0 |
|
18 Вычислить определенные интегралы методом замены переменной:
|
2 |
|
|
|
8 |
|
x |
|
4 |
|
dx |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
а) |
1 x 2 xdx ; |
б) |
|
|
|
|
dx ; |
в) |
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
x 1 |
|
0 1 |
|
2x 1 |
||||||||||
19 Вычислить определенные интегралы интегрированием по частям:
|
2 |
|
e |
1 |
а) xsinxdx ; |
б) ln xdx; |
в) xe x dx. |
||
0 |
|
1 |
0 |
|
20 Найти площадь фигуры, ограниченной линиями:
а) у = х3, у = 0, х = 1; б) у = х2, у = 1, х = 0.
33

Образцы решений
Задание 1. В пунктах а, б найти неопределенные интегралы, а в пункте в вычислить определенный интеграл.
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2x |
9 |
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
РЕШЕНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
2x 9 dx = 3 x |
3 |
|
|
|
|
2x 9 dx |
|
|
3 x |
3 dx |
2dx 9 x 2 dx = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 3 |
|
|
|
|
|
x |
3 1 |
|
|
|
|
|
|
|
|
2ln |
|
x |
|
9 |
|
|
x 2 1 |
|
С = |
3 |
|
x 3 |
|
2ln |
|
x |
|
9 |
|
x 1 |
|
С |
= |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
1 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= 93 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
С . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2ln |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
б) |
5 |
|
|
|
tg 2x |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
РЕШЕНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5 |
|
|
|
|
tg 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
tg 2x |
|
|
|
|
|
|
|
|
|
|
I1 |
+ I2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
cos2 2x |
|
|
|
cos2 2x |
|
cos2 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I1 = |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
dx |
|
= 5∙ |
|
|
dx |
|
|
= [так как |
|
|
f (ax |
b)dx |
1 |
F (ax |
b) C ] = |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
cos2 2x |
|
cos2 2x |
|
|
|
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= 5∙ |
1 |
∙tg2x + C; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
tg 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
применим подстановку tg 2x |
|
|
|
t, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
I2 = |
|
|
|
|
|
|
|
|
|
dx |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 2x |
|
= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos2 2x |
|
|
|
|
|
|
|
|
|
тогда dt |
|
|
|
|
|
dx, откуда dx |
|
|
|
|
|
dt |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 2x |
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
cos2 2x |
dt |
= |
|
1 |
|
∙ |
tdt |
= |
1 |
|
t |
2 |
+ C = |
|
1 |
tg |
2 |
|
|
2x |
|
|
C. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
cos2 |
2x |
2 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 tg 2x |
dx = |
|
5 |
tg 2x |
|
|
|
1 |
tg 2 2x C. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 2x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
в) |
|
(2х 1)sin 2xdx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

РЕШЕНИЕ
Найдѐм данный интеграл, используя формулу интегрирования по частям:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
ba |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UdV UV |
|
|
|
VdU . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
2x |
1, |
|
|
|
dV |
sin 2xdx |
|
|
|
|
|
|
|||||||
|
(2х |
|
1)sin 2xdx = |
dU |
|
(2x |
1) dx |
2dx, V |
|
|
sin 2xdx |
|
|
1 |
cos2x |
|
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(2x |
1) |
|
1 |
cos2x |
|
|
|
|
|
|
1 |
cos2x |
2dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
1 |
(2 |
1)cos2 |
|
1 |
|
1cos0 |
cos2xdx = |
|
1 |
(2 |
1) |
1 |
|
|
1 |
sin 2x |
|
||||||||||||||||
|
|
|
|
= |
|||||||||||||||||||||||||||||||
2 |
2 |
|
2 |
2 |
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
(2 |
1) |
|
sin 2 |
|
sin 0 = – π. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Задание 2. Изобразить фигуру, ограниченную указанными линиями:
у = – х, у = 2х – х2
и вычислить ее площадь.
РЕШЕНИЕ
Нарисуем чертеж фигуры, ограниченной линиями:
у = – х, у = 2х – х2.
Методом выделения полных квадратов преобразуем уравнение параболы
у= 2х – х2:
у= – (х2 – 2х), у = – (х2 – 2х + 1 – 1), у = – [(х – 1)2 – 1],
у = – (х – 1)2 + 1 или y 1 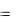 (x 1)2 .
(x 1)2 .
Из уравнения видно, что вершина параболы находится в точке (1;1), а ее ветви направлены вниз.
Прямая у = – х – это биссектриса второго и четвертого координатных углов (рисунок 3).
Рисунок 3
35
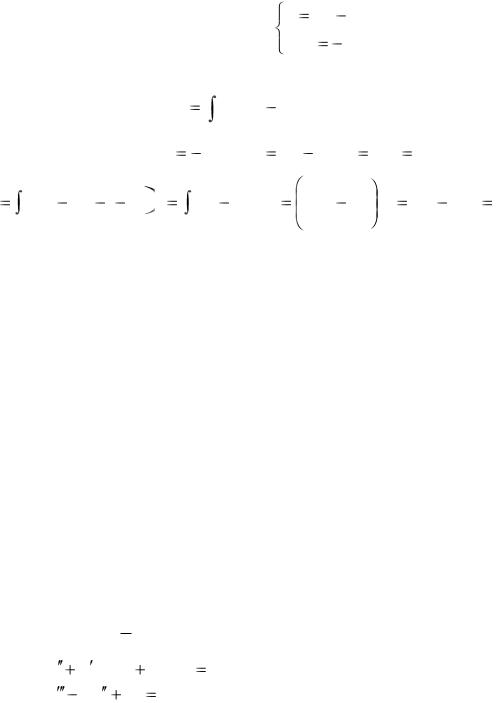
Определим абсциссы точек А и В – точек пересечения параболы и прямой. Для этого решим систему уравнений:
|
|
|
|
y |
2x |
|
x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x. |
|
|
|
|
|
|
|
|
||
Получим: хА = 0, хВ = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда по формуле S |
( f2 (x) |
f1(x))dx вычислим искомую площадь. |
|||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нашего случая f1 (x) |
x, |
f2 (x) |
2x |
x2 , a 0, b |
3. |
|
|
|
|
|
||||||
S |
3 ( 2x x2 ( x) dx |
3 (3x x2 )dx |
|
3x2 |
|
x3 |
|
|
3 |
27 |
|
27 |
|
9 |
(ед.кв.). |
|
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
2 |
3 |
|
|
|
2 |
3 |
2 |
||||||||
|
0 |
0 |
|
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема 7. Обыкновенные дифференциальные уравнения
1 Уметь определять порядок дифференциального уравнения.
2 Знать определение общего и частного решения дифференциального уравнения.
3 Знать определение дифференциального уравнения 1-го порядка с разделяющимися переменными, однородного, линейного и уметь решать их.
4 Уметь решать дифференциальные уравнения 2-го порядка, допускающие понижение порядка.
5 Знать определение общего решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами.
6 Определять вид частного решения линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.
Задачи для самостоятельного решения
1 Определить порядок дифференциального уравнения:
а) у′ + ух2 = 1x ;
б) |
у |
у cos x |
у sin x 0 ; |
в) |
у |
5 у 6 у |
0 . |
2 Показать, что функция у = Сх3 есть общее решение дифференциального уравнения ху′ – 3у = 0. Найти частное решение, удовлетворяющее условию
у(1) = 1.
3 Решить дифференциальные уравнения:
а) у′ = у2cosx;
б) у′ = |
y |
+ sin |
y |
; |
|||
x |
x |
||||||
|
|
|
|
|
|||
в) у′ + tgx = |
1 |
|
. |
||||
|
|||||||
cosx |
|||||||
36
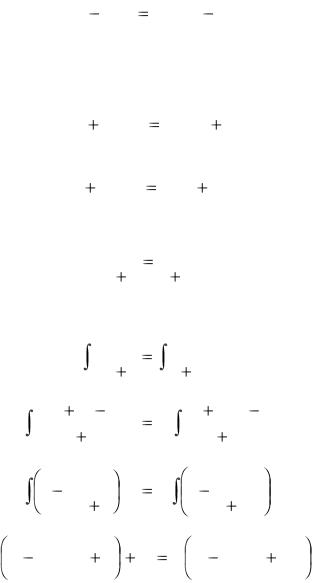
4 Найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
а) у′′ + 4у′ + 3у = 0; б) у′′ + 4у′ + 4у = 0; в) у′′ + 4у′ + 13у = 0.
5 Указать вид частного решения данного линейного неоднородного
дифференциального |
уравнения |
второго |
порядка |
с |
постоянными |
коэффициентами и специальной правой частью: |
|
|
|
||
а) у′′ + 8у′ + 16у = (1 – х)е– 4х; |
б) у′′ – 5у′ + 6у = 13sin2x; |
|
|||
в) у′′ – у = е– х; |
|
г) у′′ + 3у′ = х2 – 3. |
|
|
|
Образцы решений
Задание 1. Найти общий интеграл дифференциального уравнения первого порядка
3x dx y dy 5xy dy 2xy dx
РЕШЕНИЕ
Преобразуем данное уравнение. Слагаемые с множителем dx перенесем в левую часть равенства, а слагаемые с dy – в правую часть. Имеем:
3x dx 2xydx 5xydy ydy .
Вынесем общие множители за скобки:
x(3 2 y)dx y(5x 1)dy .
Это уравнение с разделяющимися переменными. Разделим переменные:
x dx |
y dy |
. |
||
|
|
|
|
|
5x 1 3 |
2 y |
|||
Интегрируем обе части последнего равенства:
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
|
|
|
ydy |
|
, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
5x |
1 |
|
3 |
2 y |
|
|
|
|
|||||||||||
|
|
1 |
|
|
(5x |
1) 1 |
dx |
|
1 |
|
|
|
(3 |
|
2 y) |
3 |
dy , |
|||||||||||||
|
|
5 |
|
|
|
|
5x 1 |
|
2 |
|
|
|
3 |
|
|
2 y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
1 |
|
1 |
|
dx |
|
1 |
|
|
|
1 |
3 |
|
|
dy , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5 |
5x 1 |
|
2 |
|
|
|
3 2 y |
|||||||||||||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
3 |
ln |
|
3 2 y |
|
. |
||||||||||
|
x |
|
ln |
5x 1 |
|
|
|
C |
y |
|
|
|
||||||||||||||||||
5 |
|
5 |
|
|
2 |
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, общим интегралом исходного уравнения является
37

1 |
|
1 |
|
|
1 |
|
3 |
ln |
|
3 2 y |
|
. |
||
x |
ln |
5x 1 |
C |
y |
|
|
||||||||
5 |
5 |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Задание 2. Найти общее решение линейного дифференциального уравнения первого порядка
yy sin x . x x
РЕШЕНИЕ
Так как уравнение линейное, то решаем его с помощью подстановки Бернулли:
y u  v , где u u(x), v v(x) .
v , где u u(x), v v(x) .
Имеем: y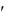 u v uv
u v uv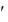 . Подставив в исходное уравнение выражения для y и y
. Подставив в исходное уравнение выражения для y и y  , получим уравнение
, получим уравнение
u v |
|
uv |
|
uv |
|
sin x |
, |
|
|
|
x |
|
x |
||||
|
|
|
|
|
|
|||
которое преобразуем к виду |
|
|
|
|
|
|
|
|
v |
v |
u |
u v |
|
sin x |
. |
||
|
|
|||||||
|
x |
|
|
|
|
x |
|
|
Так как произведение u 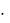 v должно удовлетворять исходному уравнению, то одну из неизвестных функций, например v , можно выбрать произвольно.
v должно удовлетворять исходному уравнению, то одну из неизвестных функций, например v , можно выбрать произвольно.
Выбираем в качестве v любое частное решение |
|
v |
v(x) уравнения v |
v |
0 . |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
dv |
|
v |
. Разделим переменные, имеем |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
dx |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv |
|
dx |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
x |
|
|
|
|
|
|
||||
Интегрируя, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dv |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
, ln |
v |
|
|
ln |
x |
|
ln C . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
v |
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
Полагая C1 |
1, выбираем частное решение v |
|
. Далее найдем общее решение |
||||||||||||||||||||||||
x |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из уравнения u v |
sin x |
, где v |
1 |
. Имеем: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
u |
sin x , |
du |
sin x , u |
sin x dx |
|
C |
cos x C . |
|
|
||||||||||||||||
|
|
dx |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
38

Общее решение исходного уравнения
y uv 1x ( sin x C) .
Задание 3. Найти общее решение уравнения
ху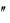 у
у ln yx
ln yx
РЕШЕНИЕ
Данное уравнение относится к уравнениям вида F (x, y , y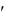 ) 0. Понизим
) 0. Понизим
его порядок с помощью подстановки |
|
|
y |
P, где P |
P(x) . |
Тогда y |
|
dP |
. |
||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
Подставив в уравнение вместо y и y |
их выражения, получим |
|
|
|
|
||||||||||||
|
|
|
|
x |
dP |
|
P ln |
P |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dx |
|
x |
|
|
|
|
|
|||||
Это однородное уравнение первого порядка относительно |
функции Р(х) . |
||||||||||||||||
Полученное уравнение решим с помощью подстановки Р |
Ux, |
P U x |
U . |
||||||||||||||
U x |
U |
U ln U |
|
|
|
|
|
||||||||||
x |
dU |
|
U (ln U |
1) |
|
|
|
|
|
|
|
||||||
dx |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разделив переменные и проинтегрировав, получим |
|
|
|
|
|
||||||||||||
|
|
dU |
|
|
|
dx |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
U (ln U |
1) |
|
x |
|
|
|
|
|
|||||||||
ln ln U 1 ln x ln C,
ln U 1 C1x, |
|
ln U C1 x 1, |
||
|
U eC1x 1, |
P xeC1x 1 , |
||
|
dy |
xeC1x 1 |
, |
dy xeC1x 1dx . |
|
|
|||
|
dx |
|||
|
|
|
|
|
Проинтегрировав, получим
dy |
|
x eC1x |
1, |
|
|
|
|
1 |
C1x |
1 |
1 |
|
C1x 1 |
y |
|
x e |
|
|
x e |
C2 . |
C1 |
|
C1 2 |
Задание 4. Найти общее решение уравнения
уу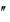 ( у )2 у 2 у
( у )2 у 2 у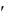 .
.
39

РЕШЕНИЕ
Данное дифференциальное уравнение второго порядка, допускающее понижение порядка, относится к уравнениям вида F ( y, y , y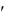 ) 0. Порядок
) 0. Порядок
такого уравнения понижается подстановкой у Р , где Р Р( у). Тогда
Р , где Р Р( у). Тогда
у |
dP |
|
dy |
P |
dP |
. |
|
|
|
|
|||
|
dу |
|
dx |
|
dy |
|
Подставляя вместо y и y
и y их выражения в исходное уравнение, получим
их выражения в исходное уравнение, получим
уР |
dP |
|
P 2 |
у 2 Р |
||
dу |
||||||
|
|
|
||||
или |
|
|
||||
у |
dP |
P |
у2 |
|||
dу |
||||||
|
|
|
. |
|||
|
|
|
|
|
||
Получили линейное дифференциальное уравнение первого порядка относительно искомой функции Р( у).
Решаем подстановкой Р U V , P U V |
V U . |
y(U V V U ) UV y 2 , |
|
y U V U (V y V ) |
y 2 . |
Функцию V выберем так, чтобы коэффициент при U был равен нулю.
|
y |
dV |
|
V 0 |
|
или |
dV |
|
dy |
|
||||||
dy |
|
|
V |
|
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dV |
|
dy |
; |
|
|
ln V |
|
ln y, |
|
|
V y. |
||||
|
|
|
|
|
|
|
||||||||||
|
V |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя V y в уравнение, получим |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
y |
2 dU |
y |
2 |
, |
( y |
0) |
|
|
|
||
|
|
|
|
|
|
dy |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dU |
dy, |
|
U y |
C1 . |
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
P ( y |
C1 ) y |
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dy |
y( y C1 ). |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделив переменные и проинтегрировав, получим |
|
|
|
||||||||||||||
|
|
|
|
|
dy |
|
|
|
|
1 |
|
|
y |
|
|
||
|
|
|
|
|
dx, |
|
|
|
ln |
|
|
x C2 |
|||||
|
|
|
|
|
y( y C1 ) |
|
|
|
|
С1 |
y C1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ln |
|
y |
C1 |
(x C2 ) – общий интеграл данного уравнения при Р 0. |
|||||||||||||
|
|
||||||||||||||||
y |
C1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
