
МУ для подготовки к АКР 1 семестр выс. мат
..pdf
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
lim 3 |
lim |
4 |
lim |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
x |
x |
2 |
|
|
||||||||||
|
|
|
3x2 |
4x 2 |
|
|
|
|
|
|
|
x |
x |
|
|
x |
|
|
|
||||||
|
|
|
|
|
x |
|
x2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
lim |
|
|
|
= ( |
|
) = lim |
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
||||
|
8 |
x2 |
|
|
8 |
|
|
|
8 |
|
|
|
|
|
|||||||||||
|
x |
|
|
|
x |
1 |
|
|
lim |
|
|
lim 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
x2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|||
= |
3 0 |
0 |
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б) lim |
|
9 |
x |
|
3 |
. |
|
|
||
|
|
x2 |
|
|
x |
|
|
||||
|
|
x 0 |
|
|
|
|
|
|
|||
|
Так как lim ( |
|
|
3) = 0 и lim (x2 x) = 0, то имеем неопределенность |
|||||||
|
9 x |
||||||||||
|
|
|
|
x |
0 |
|
|
|
|
|
x 0 |
типа |
0 |
. |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем выражение под знаком предела, домножив числитель и |
||||||||||
|
|
|
|
|
|
|
|||||
знаменатель на ( |
9 |
|
х |
3) – выражение, сопряженное числителю. |
|||||||
|
|
|
|
9 |
|
х |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||||
lim |
|
|
|
= ( |
0 |
|
) = lim |
|
( 9 х 3) ( 9 х 3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
( 9 х ) |
3 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x |
0 |
х |
2 |
|
|
x |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
х(х 1) ( 9 х 3) |
|
|
|
|
|
x 0 х(х 1) ( 9 х 3) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
= lim |
|
|
|
|
|
9 |
|
|
|
|
х |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
x 0 х(х 1) ( 9 х 3) |
|
|
|
|
x 0 х(х 1) ( 9 х 3) |
|
|
|
x 0 |
|
(х 1) ( 9 х 3) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim (х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1) |
|
lim ( |
9 |
|
|
х |
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
x |
0 |
|
|
|
|
|
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
в) |
lim |
|
|
sin 2 |
х |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x |
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Так как lim sin 2 x = 0 и lim (1 |
|
cos x) |
0 , то имеем неопределенность типа |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
. |
Для |
|
|
раскрытия |
|
|
этой |
|
|
|
|
неопределенности |
|
|
|
|
используем |
|
формулу |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
cosx |
2sin |
2 x |
и первый замечательный предел lim |
|
sin x |
= 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 x |
|
|
|
x |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
lim |
|
sin 2 х |
|
|
|
= ( |
|
0 |
) = |
lim |
|
|
sin 2 x |
|
= |
1 |
|
lim |
|
|
2 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
0 1 |
cos x |
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
|
0 |
2sin |
2 x |
2 |
|
x |
0 |
|
|
x |
2 |
sin |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
=2 |
|
lim |
|
|
|
lim |
|
|
2 |
|
|
|
|
|
= 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
|
x |
2 |
|
|
|
2 x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
lim |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Так как |
lim |
|
x |
2 |
= 1, |
lim (2x |
1) = ∞, то имеем неопределенность типа |
|||||||||||||||||||
|
|
|
x |
3 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
1 . Используем второй замечательный предел: |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
|
|
|
= е. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
x 2 2 x 1 |
|
|
|
|
|
|
|
x 2 |
|
2 x 1 |
|
|
|
x 2 x 3 2 x 1 |
|||||||||||||
lim |
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
1 |
= lim 1 |
|
|
|
|
= |
|||||||||
|
x |
3 |
|
|
|
|
|
x |
3 |
|
|
x 3 |
||||||||||||||||
x |
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 x 1 |
|
|
||
|
|
|
|
|
|
|
|
2 x 1 |
|
|
|
|
|
|
|
|
( x 3) |
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
( x 3) |
1 |
|
||||||||||||
= lim |
1 |
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
|
|
|
= е– 2 = |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
x |
3 |
|
|
|
|
|
x |
|
|
|
|
(x |
3) |
|
|
|
|
|
|
|
e2 |
|||
|
|
д) lim |
|
tg3x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x 0 e2 x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычислим |
предел |
lim |
|
tg3x |
, |
||
|
|
|
|||||
|
|
|
x 0 e2 x |
1 |
|
||
малые функции при x |
x0 . |
|
|
|
|
||
Если при х |
х0 |
(x) |
|
*(x) , |
в(x) |
||
lim |
(x) |
lim |
* (x) |
|
(x) |
(x) |
|||
x x0 |
x x0 |
|||
Поэтому |
|
|
|
используя |
эквивалентные бесконечно |
|||||
* (x) , тогда |
|
|
||||
lim |
(x) |
|
lim |
* (x) |
. |
|
* (x) |
* (x) |
|||||
x x0 |
x x0 |
|
||||
lim |
|
tg3x |
|
tg3x 3x, (e2 x 1) |
2х, при х |
0 |
|
= lim |
3x |
|
3 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||
x 0 e2 x 1 |
|
|
|
|
|
x 0 |
2x 2 |
||||||
|
|
|
|
|
|||||||||
Задание 2. |
Исследовать функцию |
у f (x) |
на непрерывность: найти |
||||||||||
точки разрыва и определить их тип. Изобразить схематический график функции.
|
|
x, |
x |
0, |
|
|
|
|
f (x) = x2 , 0 x 2, |
|
|
||||
|
|
2, |
x |
2 |
|
|
|
РЕШЕНИЕ |
|
|
|
|
|
|
|
x, |
x |
0, |
|
y1 |
x, |
x |
0, |
f (x) = x2 , 0 x 2, |
|
y2 |
x2 , 0 x 2, |
||||
2, |
x |
2. |
|
y3 |
2, |
x |
2. |
|
|
22 |
|
|
|
|
|

На каждом из промежутков (– ; 0); (0; 2); (2; + ) функция определена и является элементарной и, следовательно, непрерывна. Непрерывность функции может нарушаться лишь в точках, где меняется ее аналитическое задание, т.е. в точках х = 0 и х = 2. Исследуем функцию на непрерывность в этих точках. Найдем односторонние пределы функции в точках х = 0 и х = 2.
Если х = 0, то имеем:
|
|
|
lim |
f (x) |
lim |
( х) |
0 ; |
|
|
x 0 |
x |
0 |
|
|
|
|
|
|
lim |
f (x) |
lim |
х2 |
0; |
|
|
|
x |
0 |
x |
0 |
|
|
|
|
|
f (0 ) = 0. |
|
||
Так как, f (0) = lim |
f (x) |
= lim |
f (x) , то функция непрерывна в т. х = 0. |
||||
x |
0 |
x |
0 |
|
|
|
|
Если х = 2, то имеем:
|
lim |
|
f (x) = |
lim |
x 2 = 4; |
x |
2 |
0 |
x |
2 0 |
|
|
lim |
|
f (x) = |
lim |
2 = 2; |
x |
2 |
0 |
x 2 |
0 |
|
|
|
|
f (2) = 4. |
|
|
Так как в точке х = 2 односторонние пределы функции не равны между собой, то эта точка является точкой разрыва функции. А так как эти пределы являются конечными числами, то это точка разрыва первого рода.
Сделаем чертеж.
y
4
3
y |
2 |
x2 |
y3 2 |
y1 x |
2 |
1
|
|
|
|
|
|
|
|
|
|
|
|
х |
-2 |
-1 |
|
1 |
2 |
3 |
|
||||||
-1
Рисунок 1 – График функции f (x)
23
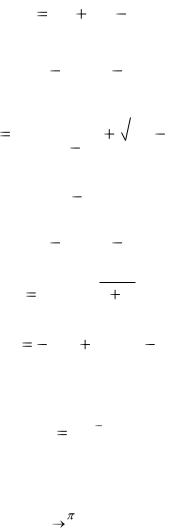
Тема 3. Дифференциальное исчисление функции одной переменной
1 Знать и применять формулы для нахождения производной суммы, разности, произведения, частного двух функций.
2Находить производную сложной функции.
3Находить дифференциал функции у = f(х) в заданной точке.
4Находить пределы, используя правило Лопиталя.
5Уметь находить точки экстремума.
6Определять интервалы выпуклости вверх и выпуклости вниз графика функции.
7Определять точки перегиба графика функции.
8Находить вертикальные и наклонные асимптоты графика функции.
9Строить графики функций с использованием производной.
Задачи для самостоятельного решения
1 Найти производную функции:
y |
x3 |
3 |
4. |
|
3 |
|
x3 |
||
|
|
|
||
2 Найти производную функции:
y 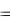 sin(5x 4). 3 Найти производную функции:
sin(5x 4). 3 Найти производную функции:
|
5x7 |
3 |
|
|
||
y |
x2 |
1. |
||||
cos(6x |
3) |
|
||||
|
|
|
|
|||
4 Найти производную третьего порядка функции: y 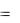 12 x2 .
12 x2 .
5 Найти производную третьего порядка функции: y 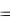 sin(5x 4).
sin(5x 4).
6 Найти производную функции:
y (arctg 
 1 x )2 .
1 x )2 .
7 Найти дифференциал функции:
f (x) |
2x2 sin( 2x 11). |
8 Найти дифференциал второго порядка d 2 y ,если x – независимая переменная для функции:
y |
1 |
e 7 x . |
|
7 |
|||
|
|
9 Используя правило Лопиталя, вычислить предел:
lim |
|
tg 4x |
. |
|
|
|
|||
x |
|
|
tg8x |
|
|
|
|
|
|
2 |
|
|
|
|
10 Используя правило Лопиталя, вычислить предел:
24
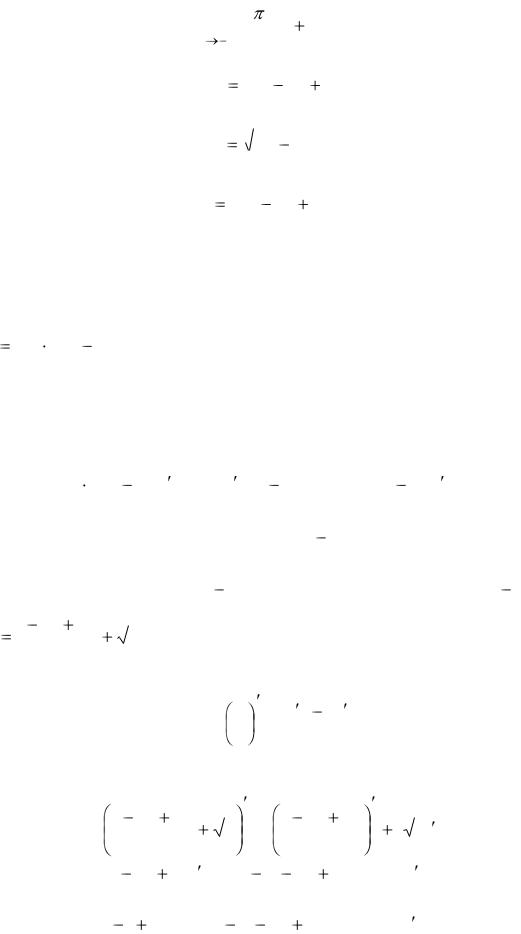
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim tg |
|
|
x |
(x |
3). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11 Исследовать функцию на возрастание и убывание: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 3x3 |
|
|
|
|
8x |
1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12 Найти экстремум функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
13 Исследовать на выпуклость и точки перегиба график функции: |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
3x6 |
|
6x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Образцы решений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Задание 1. Найти производные у′ = |
|
dy |
|
|
данных функций. |
|
|
|
|
||||||||||||||||||||||||||||||||
|
dx |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) у 57 x |
tg(1 |
3x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Производную данной функции найдем по формуле |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
у′ = (u∙v)′ = u′v + uv′, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
где u = u(х) и v = v(х) – дифференцируемые функции. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
у′ = (57 x |
tg(1 |
|
3x)) |
= (57 x ) tg(1 |
|
|
|
3x) + 57 x (tg(1 |
3x)) |
= |
|
|||||||||||||||||||||||||||||
|
|
= 57х∙ln5∙(7x)′∙tg(1 – 3x) + 57х∙ |
|
|
|
|
|
|
|
|
1 |
|
|
∙(1 – 3x)′ = |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
cos2 (1 |
3x) |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
= 7∙57х∙ln5∙tg(1 – 3x) – 3∙57х∙ |
|
|
|
|
|
|
= 57х(7ln5∙tg(1 – 3x) – 3∙ |
|
). |
||||||||||||||||||||||||||||||||
cos2 (1 |
3x) |
|
cos2 (1 3x) |
||||||||||||||||||||||||||||||||||||||
б) y |
1 |
3x x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
sin 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Производную данной функции найдем, используя формулу |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
у′ = |
|
u |
|
= |
|
|
u v |
uv |
, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где u = u(х) и v = v(х) – дифференцируемые функции. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
у′ = |
1 |
|
3x |
x2 |
|
|
|
|
= |
|
|
|
1 |
|
3x |
x2 |
|
|
|
|
|
= |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
( |
5) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 4x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
= |
|
(1 |
|
3x |
x2 ) sin 4x |
(1 |
|
|
|
3x |
x2 )(sin 4x) |
= |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 4x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
= |
( |
3 2x)sin 4x |
(1 |
|
|
3x |
x2 )cos4x(4x) |
= |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

= |
(2x 3)sin 4x 4(1 3x |
x2 )cos4x |
. |
sin 2 4x |
|
||
|
|
|
в) у = (arctg2x + 3е2x – 5x)4.
Данная функция является сложной и ее можно записать в виде у = и4, где и = arctg2x + 3е2x – 5x. Производную сложной функции найдем по правилу
ух′ = уи′их′.
Тогда
у′ = ((arctg2x + 3е2x – 5x)4)′ = 4(arctg2x + 3е2x – 5x)3(arctg2x + 3е2x – 5x)′ =
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4(arctg2x + 3е2x – 5x)3( |
|
2 |
|
|
+ 6е2х – 5). |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4х2 |
|
|||||||||||||||||||||||
|
Задание 2. Используя правило Лопиталя, найти пределы: |
|
|||||||||||||||||||||||||||||||||||||||
|
а) lim |
sin 5x |
; |
|
|
|
|
|
|
|
б) lim |
|
x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
0 sin 3x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
РЕШЕНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Согласно правилу Лопиталя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
u(x) |
= lim |
u (x) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v(x) |
v (x) |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
x x0 |
|
|
|
|
|
|
|||||||||||||
для неопределенностей вида |
|
0 |
и |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда в нашем случае: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
а) lim |
sin 5x |
= |
|
0 |
= lim |
(sin 5x) |
|
= lim |
5cos5x |
= |
|
5 |
. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x 0 sin 3x |
x 0 |
(sin 3x) |
|
x |
0 |
3cos3x |
3 |
|
|
|
|
|||||||||||||||||||||||||||||
б) |
|
lim |
|
x2 |
|
= |
|
|
|
|
= lim |
(x2 ) |
|
= |
|
|
lim |
|
2x |
= |
|
|
|
|
= lim |
(2x) |
|
= |
|||||||||||||
|
|
ex |
|
|
|
|
(ex ) |
|
|
|
ex |
|
|
|
|
(ex ) |
|||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||
= lim |
|
2 |
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
e x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задание 3. Найти интервалы возрастания и убывания функции у = 3х – х2.
РЕШЕНИЕ
Для нахождения интервалов возрастания и убывания функции используется следующий алгоритм:
1)Находим область определения функции D(у).
2)Находим производную заданной функции.
3)Приравниваем производную к нулю и находим корни получившегося уравнения.
26

4)Найденными точками разбиваем область определения функции на интервалы и находим знак производной на каждом из них.
5)Если на интервале знакопостоянства у′ < 0, то функция на этом интервале убывает, и наоборот – если у′ > 0, то функция на этом интервале возрастает.
Следуя алгоритму, получаем:
D(у) = R.
Находим производную функции:
|
|
|
|
|
|
|
у′ = (3х – х2)′ = 3 – 2х. |
|
|
|
|
||
|
В области определения |
функции |
у′ = 0 при 3 – 2х = 0, |
т.е. при х = |
3 |
. |
|||||||
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найденная |
точка |
разбивает |
область |
определения функции |
на |
интервалы |
|||||||
(– ∞; |
3 |
) и ( |
3 |
; + ∞). |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
+ |
1,5 |
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
В интервале |
(– ∞; |
3 |
) |
производная у′ < 0, следовательно, |
функция |
|
в |
|||||
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данном интервале убывает, а в интервале ( 32 ; + ∞) у′ > 0 – функция возрастает.
Тема 4. Функции нескольких переменных
1 Находить значение функции двух переменных в точке.
2Находить частные производные функции двух переменных.
3Уметь находить полный дифференциал функции двух переменных в заданной точке.
4Определять локальные экстремумы функции двух переменных.
Задачи для самостоятельного решения
1 Найти частные производные функции двух переменных: z = x3 + y3 – 5xy – x2y + 2xy2.
2 Найти частные производные второго порядка функции двух переменных:
z = 3y∙сos(7x + 2y).
3 Найти локальные экстремумы функции двух переменных: z = 8x2 – y2 + 2x + 2y.
Образцы решений
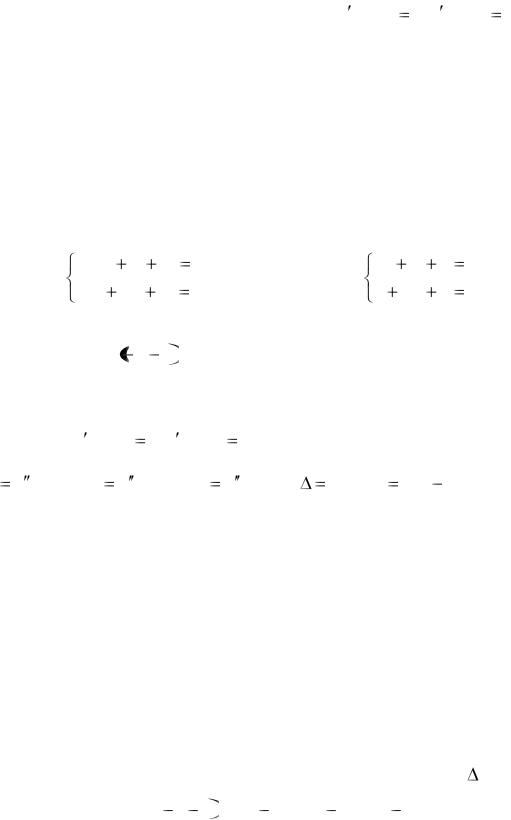
Задание 1. Найти локальные экстремумы функции двух переменных z = x 2 y xy 2 3xy (x 0; y 0) .
27
РЕШЕНИЕ
Так как по условию x < 0, y < 0, то областью определения функции двух переменных является часть плоскости, лежащая внутри третьей четверти, не включая осей координат.
Если дифференцируемая функция z = f(x,y) имеет в точке М0(х0; у0) локальный экстремум, то в этой точке обе ее частные производные первого порядка, если они существуют, равны нулю, т.е. zx (M 0 ) 0, z у (M 0 ) 0 , либо
хотя бы одна из этих частных производных в этой точке не существует.
Точки, принадлежащие области определения, в которых частные производные равны нулю или хотя бы одна из них не существует, называются
критическими.
Находим частные производные данной функции:
|
|
zx′ = 2xy + y2 +3y, |
|
|
|
|
|
zy′ = x2 + 2xy +3 x. |
|
|
|
Приравнивая их к нулю, получаем систему уравнений: |
|
|
|||
y(2x |
y |
3) 0, |
Т.к. x<0 и y<0, то |
2x y 3 |
0, |
x(x 2 y 3) 0. |
|
x 2 y 3 0. |
|||
Полученная система имеет одно решение, которое определяет |
|||||
критическую точку: М0 |
1; |
1 . |
|
|
|
Рассмотрим достаточные |
условия существования |
локального |
|||
экстремума. Пусть существуют частные производные первого и второго
порядков |
функции |
z = f (x; y) |
и М0(х0; у0) – критическая |
точка функции |
||||||
z = f (x; y), то есть zx (M 0 ) 0, z у (M 0 ) |
0 . Введем следующие обозначения: |
|||||||||
A |
zxx(M 0 ), |
B zxy(M 0 ), |
C |
z yy(M 0 ), |
|
A |
B |
|
AC |
B2. |
|
|
|||||||||
|
B |
C |
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Тогда:
1)если > 0, A > 0 (или C > 0), то функция имеет в точке М0 минимум;
2)если > 0, A < 0 (или C < 0), то функция имеет в точке М0 максимум;
3)если < 0, то в точке М0 экстремума нет;
4)если = 0, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Вычислим частные производные второго порядка функции z = f (x,y):
zxx″ = 2y; zxy″ = 2x + 2y + 3;
zyy″ = 2x,
и для критической точки М0 вычисляем соответствующее значение :
M 0 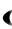 1; 1 : A
1; 1 : A 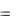 2, B
2, B  1, C
1, C 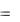 2,
2,
28

тогда
(M0 ) |
2 |
1 |
3 > 0, |
A 2 0 , |
|
1 |
2 |
||||
|
|
|
то в точке М0 имеем точку локального максимума функции, в которой
Zmax (–1; –1) = 1.
Тема 5. Комплексные числа
1 Знать определение комплексного числа и уметь выполнять действия над комплексными числами в алгебраической форме.
2 Указывать комплексное число, сопряженное данному комплексному числу.
3Изображать комплексные числа на плоскости.
4Определять модуль и аргумент комплексного числа.
5Представлять комплексные числа в тригонометрической форме и выполнять действия над комплексными числами в тригонометрической форме.
6Представлять комплексные числа в показательной форме.
7Возводить в натуральную степень и извлекать корни натуральной степени из комплексных чисел.
Задачи для самостоятельного решения |
|
|
|
|
|
|
|
|
|
|||||||
1 |
Дано комплексное число z |
3 |
2i . Действительная часть комплексного |
|||||||||||||
числа равна … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Дано комплексное число z |
3 |
2i . Мнимая часть комплексного числа |
|||||||||||||
равна … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
Дано комплексное число z |
2 |
i . Комплексное число z , сопряженное |
|||||||||||||
данному, равно … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Сумма комплексных чисел z1 |
1 2i |
и z2 |
2 |
4i |
равна … |
||||||||||
5 |
Разность комплексных чисел z1 |
2 |
5i и z2 |
3 |
2i равна … |
|||||||||||
6 |
Произведение комплексных чисел z1 |
2 |
2i и z2 |
|
4 |
4i |
равно … |
|||||||||
7 |
Частное комплексных чисел z1 |
1 |
2i и z2 |
2 |
|
4i |
равно … |
|||||||||
8 |
Комплексное число z1 |
1 |
2i |
изображается точкой с координатами … |
||||||||||||
либо радиус-вектором … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9 |
Дано комплексное число z1 |
1 |
|
3i . Модуль |
числа |
|
z |
равен …, |
||||||||
аргумент этого числа равен … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 Тригонометрическая форма комплексного числа z |
|
1 i |
… |
|||||||||||||
11 Показательная форма комплексного числа z |
1 |
i |
… |
|
|
|
||||||||||
29
Образцы решений
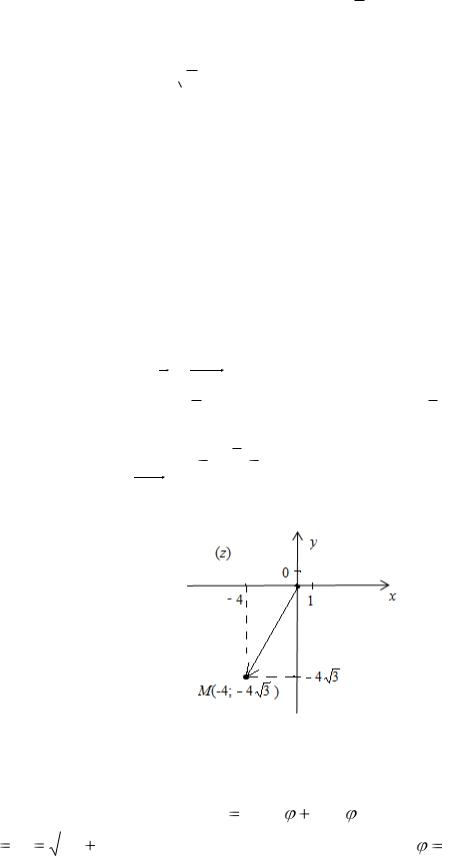
Задание 1. Дано комплексное число z = – 4 
 3 – 4∙i.Требуется:
3 – 4∙i.Требуется:
1)изобразить число z в виде радиус-вектора на комплексной плоскости;
2)записать число z в тригонометрической форме;
3)найти все значения 3 z .
z .
РЕШЕНИЕ
1) Комплексным числом называется число z = x + i∙y, где х и у –
действительные числа, а i – мнимая единица, i2 = – 1.
х= Rez называется действительной частью комплексного числа, а у = Imz
–мнимой частью комплексного числа.
Запись числа в виде z = x + i∙y называется алгебраической формой комплексного числа.
Всякое комплексное число z = x + i∙y можно изобразить точкой М(х; у) плоскости Оху такой, что х = Rez, у = Imz. Плоскость, на которой изображается комплексное число, называется комплексной плоскостью, при этом ось абсцисс называют действительной осью, а ось ординат – мнимой осью.
Комплексное число изображают также на комплексной плоскости с помощью радиус-вектора r = OM = (х; у).
В нашем случае z = – 4 
 3 – 4∙i. Имеем х = Re z = – 4
3 – 4∙i. Имеем х = Re z = – 4 
 3 , у = Im z = – 4. Изобразим это число на комплексной плоскости в виде радиус-вектора.
3 , у = Im z = – 4. Изобразим это число на комплексной плоскости в виде радиус-вектора.
Для этого построим точку M ( 4
 3; 4) и соединим ее с началом координат.
3; 4) и соединим ее с началом координат.
Тогда радиус-вектор OM изображает число z на комплексной плоскости (рисунок 2).
|
|
|
|
|
|
|
|
|
Рисунок 2 |
|
|
2) Запишем число z |
в тригонометрической форме |
|
|||||||||
|
|
|
|
|
|
|
|
z |
r(cos i sin |
) , |
|
|
|
|
|
|
|
|
|
||||
где r |
|
z |
|
x 2 |
y 2 – |
модуль комплексного |
числа, |
arg z – аргумент |
|||
|
|
||||||||||
комплексного числа z . |
|
|
|
|
|
||||||
Аргумент |
комплексного |
числа z ≠ 0 – |
величина |
многозначная и |
|||||||
определяется |
с |
точностью |
до |
слагаемого |
2πk (k = 0,– 1, 1, – 2, 2 …): |
||||||
|
|
|
|
|
|
|
|
|
30 |
|
|
