
МУ для подготовки к АКР 1 семестр выс. мат
..pdf
Задание 6. Проверить, является ли система линейных уравнений
х1  х2
х2 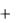 х3
х3  4 ,
4 ,
х1 2х2 4х3 4, х1 3х2 9х3 2.
совместной и решить ее, в случае совместности:
а) решить систему по формулам Крамера;
б) матричным методом. Проверить правильность нахождения обратной матрицы матричным умножением (АА – 1 = А – 1А = Е);
в) методом Гаусса.
РЕШЕНИЕ
Совместность данной системы докажем, используя теорему Крамера, а именно: если главный определитель системы отличен от нуля, то система имеет единственное решение. Определитель системы
1 1 1 = 1 2 4 = 18 + 3 + 4 – 2 – 12 – 9 = 2 0.
1 3 9
Значит, система совместная.
а) Решим систему уравнений по формулам Крамера:
х |
1 |
, у |
2 |
, z |
3 |
, |
|
|
|
где ∆1, ∆2, ∆3 – определители, которые получаются из определителя системы ∆ посредством замены свободными членами элементов соответственно первого, второго и третьего столбцов.
|
1 |
1 |
1 |
|
= |
1 |
2 |
4 |
= 2. |
|
1 |
3 |
9 |
|
|
|
|
|
|
Вычислим ∆1, ∆2, ∆3:
4 |
1 |
1 |
1 |
4 |
1 |
1 |
1 |
4 |
1 = 4 |
2 4 = 4; 2 = 1 |
4 |
4 = 6; |
3 = 1 |
2 4 = – 2. |
||||||||
2 |
3 |
9 |
|
1 |
2 |
9 |
1 |
3 |
2 |
||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 = |
1 |
4 |
= 2; х2 = |
2 |
|
6 |
= 3; х3 = |
3 |
|
2 |
= – 1. |
||
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
2 |
|
|
|
2 |
||||
Ответ: х1 = 2, х2 = 3, х3 = – 1.
б) Решим систему линейных уравнений матричным методом. Введем обозначения:
11

1 |
1 |
1 |
х1 |
|
А = 1 |
2 |
4 |
– матрица системы, Х = х2 |
– матрица-столбец из неизвестных, |
1 |
3 9 |
х |
|
|
|
|
|
3 |
|
4
В = 4 – матрица-столбец из свободных членов системы.
2
Тогда заданную систему можно записать в виде: АХ = В, откуда Х = А– 1В, где А– 1 – обратная матрица. Найдем А– 1, зная, что
|
|
A11 |
A21 |
A31 |
|
А– 1 = |
1 |
A12 |
A22 |
A32 , |
|
|
|||||
det A |
|||||
|
A13 |
A23 |
A33 |
||
|
|
где Аij – алгебраические дополнения элементов аij матрицы А.
А |
( 1)i j M |
ij |
, |
ij |
|
|
где Mij – миноры элементов аij матрицы А.
Вычислим определитель матрицы коэффициентов системы
|
1 |
1 |
1 |
|
det A = |
1 |
2 |
4 |
= 2. |
|
1 |
3 |
9 |
|
|
|
|
|
|
Так как det A 0 , то существует обратная матрица. Найдем ее.
|
|
|
|
|
|
|
1+1 |
|
2 |
4 |
|
|
|
18 |
2 6 , А12 = – 5, А13 = 1, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
А11 = (–1) |
|
|
3 |
9 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
А21 |
=(–1) |
2+1 |
|
1 |
1 |
|
|
|
|
|
(9 |
3) |
|
6 , А22 = 8, А23 = – 2, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
3 |
9 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3+1 |
|
1 |
1 |
|
|
|
4 2 2 |
, А32 = – 3, А33 = 1. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
А31 = (–1) |
|
|
2 |
4 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
6 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
А– 1 = |
5 |
|
8 |
3 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Проверим правильность вычисления обратной матрицы, используя |
||||||||||||||||||||||||
матричное умножение, т.е. АА– 1 = А– 1А = Е. |
|
|
|
|
|
|
|||||||||||||||||||
1 |
1 |
1 |
|
|
|
6 |
6 |
|
|
2 |
|
|
|
|
|
6 |
5 |
1 |
6 |
8 |
2 |
2 |
3 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||||||||||||
1 2 4 |
∙ |
∙ |
5 8 3 |
= |
|
∙ 6 10 4 |
6 16 8 |
2 6 4 = |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||
1 |
3 |
9 |
2 |
|
1 |
2 |
|
|
1 |
|
|
2 |
|
6 |
15 |
9 |
6 |
24 |
18 |
2 |
9 |
9 |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|

|
1 |
2 |
0 |
0 |
1 |
0 |
0 |
|
|
= |
∙ 0 |
2 |
0 |
= 0 |
1 0 |
= Е. |
|||
2 |
|||||||||
|
0 |
0 |
2 |
0 |
0 |
1 |
|
||
|
|
|
|||||||
Аналогично доказывается, что А– 1А = Е. Значит, матрица А– 1 найдена верно. Тогда
|
|
|
1 |
|
6 |
6 |
|
2 |
|
4 |
|
1 |
|
|
24 |
24 |
4 |
|
1 |
|
4 |
|
2 |
|
|
|||
Х = А– 1В = |
∙ |
5 8 3 ∙ 4 |
= |
∙ |
20 32 6 = |
∙ |
6 |
= 3 . |
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
1 |
2 |
|
1 |
|
2 |
2 |
|
|
4 |
8 |
2 |
|
2 |
|
2 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Таким образом, |
х1 = 2; |
х2 = 3; |
|
х3 = –1, тройка чисел {2, 3, –1} является |
|||||||||||||||||||||||
решением системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ответ: {2, 3, –1}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
в) Решим систему линейных уравнений методом Гаусса. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
Первое уравнение системы умножим на ( |
1) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
х1 |
х2 |
х3 |
4, |
|
|
и сложим со вторым уравнением, результат |
|
|||||||||||||||||||||
|
|
сложения запишем вторым уравнением в новой |
|
|||||||||||||||||||||||||
х1 |
2х2 |
4х3 |
4, |
|
|
|
||||||||||||||||||||||
|
|
системе. Затем первое уравнение системы умножим |
|
|||||||||||||||||||||||||
х1 |
3х2 |
9х3 |
2, |
|
|
|
||||||||||||||||||||||
|
|
на ( 1) и сложим с третьим уравнением системы, |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
результат запишем третьим уравнением. |
|
|
|
|||||||||||||||||
|
х1 |
х2 |
х3 |
4, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Умножим второе уравнение системы на ( 2) |
|
||||||||||||||||||||||
|
|
|
|
|
и сложим с третьим уравнением, результат |
|
|
|||||||||||||||||||||
|
х2 |
3х3 |
0, |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
запишем третьим уравнением эквивалентно |
|
|
|||||||||||||||||||||
|
|
2х2 |
8х3 |
2, |
|
|
||||||||||||||||||||||
|
|
|
преобразованной системы. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
х1 |
х2 |
х3 |
4, |
|
|
|
х1 |
4 х2 |
|
х3 , х1 |
4 х2 |
х3 , |
|
х1 |
2, |
|
|
||||||||||
|
х2 |
3х3 |
0, |
|
|
|
х2 |
|
3х3 , |
|
|
|
х2 |
3х3 , |
|
|
|
х2 |
3, |
|
|
|||||||
|
|
|
2х3 |
2, |
|
|
|
х3 |
|
|
1. |
|
|
|
|
х3 |
1. |
|
|
|
|
х3 |
1. |
|
|
|||
|
Ответ: {2, 3, –1}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Задание 7. Найти длину вектора AB , если А(1; 2; 3), В(4; 6; 3). |
|||||||||||||||||||||||||||
|
РЕШЕНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Для нахождения длины заданного вектора вначале найдем его |
|||||||||||||||||||||||||||
координаты |
по |
формуле |
AB = (хВ – хА; уВ – уА; zВ – zА), |
где |
A(хА; yА; zА) и |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
В(хВ; yВ; zВ). Затем по формуле |
a |
= |
|
|
a |
2 |
a 2 |
a 2 , где а1, а2, а3 – координаты |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|||
вектора a = (а1; а2; а3), найдем его длину. В нашем случае имеем:
13

AB = (4 – 1; 6 – 2; 3 – 3) = (3; 4; 0), |
тогда, подставляя координаты в |
||||||
формулу нахождения длины вектора, получаем: |
|||||||
|
|
|
|
|
|
|
|
| AB | = 32 42 02 = |
|
|
|
|
|||
9 16 0 |
= 25 = 5. |
||||||
Задание 8. Вычислить скалярное |
произведение векторов ( a ,b ), если |
||||||
a = (8; 4; 9) и b = (2; 6; 1). |
|
|
|
|
|||
РЕШЕНИЕ
Для вычисления скалярного произведения векторов пользуются следующей формулой:
( a , b ) = a ∙ b = а1b1 + а2b2 + а3b3,
где а1, а2, а3 – координаты вектора a , а b1, b2, b3 – координаты вектора b . В нашем случае имеем:
a ∙b = 8∙2 + 4∙2 + 9∙1 = 16 + 24 + 9 = 49.
Задание 9. Найти cosα между векторами a = (2; 1; 3) и b = (1; 3; 2).
РЕШЕНИЕ
Для того чтобы найти косинус угла между векторами, воспользуемся следующей формулой:
cosα = a 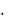 b , a
b , a
 b
b
где в числителе стоит скалярное произведение данных векторов (см. пример 8), а в знаменателе произведение их длин (см. пример 7). Найдем вначале скалярное произведение данных векторов:
a ∙ b = 2∙1 + 1∙3 + 3∙2 = 2 + 3 + 6 = 11.
Теперь найдем их длины:
| a | = 22 |
12 |
32 = |
|
|
|
|
|
|
|
|
||
4 1 9 |
= 14 ; |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
| b | = 12 |
32 |
22 = |
|
|
|
|
||||||
1 9 4 |
= 14 . |
|||||||||||
Подставляем найденные значения в формулу:
cosα = |
a |
|
b |
= |
11 |
|
|
= |
|
11 |
. |
||
|
|
|
|
|
|
|
|
14 |
|||||
|
a |
|
b |
|
14 14 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 10. По координатам вершин пирамиды А1 А2 А3 А4 найти:
а) косинус угла между ребрами А1А2 и А1А4;
б) площадь грани А1А2А3; в) объем пирамиды;
14

г) уравнение плоскости А1А2А3; д) уравнение высоты, опущенной из точки А4 на грань А1А2А3, и ее длину.
А1(0; 4; 5); А2(3; – 2; 1); А3(4; 5; 6); А4(3; 3; 2).
РЕШЕНИЕ
а) Угол между ребрами А1 А2 и А1 А4 находим как угол между двумя векторами А1 А2 и А1 А4 . Для этого требуется знать координаты векторов А1 А2 и
А1 А4 . Найдем их: |
|
|
|
|
|
|
|
||
А1А2 |
= (х2 |
х1; у2 |
y ; |
z2 |
z1 ) = (3 – 0; 2 |
– 4; 1 |
– 5) = (3; – 6; – 4); |
||
|
|
|
|
|
1 |
|
|
|
|
А1 А4 |
= (х |
4 |
х1; у |
4 |
y ; |
z4 |
z1 ) = (3 – 0; 3 |
– 4; 2 |
– 5) = (3; – 1; – 3). |
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Косинус угла между двумя векторами а = (а1; а2; а3) и b = (b1; b2; b3) найдем по формуле
cos |
ab |
|
|
а1b1 |
а2b2 |
а3b3 |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
||
a |
|
b |
|
|
а12 а22 |
а32 |
b12 b22 b32 |
||||
|
|
|
|
|
|
||||||
Для данных векторов имеем:
cos |
|
|
9 |
6 |
12 |
|
|
27 |
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
36 |
16 |
9 |
1 |
9 |
61 |
19 |
|
|
||||||||
б) Известно, что модуль векторного произведения a b численно равен
площади параллелограмма, построенного на векторах a и b . Тогда площадь треугольника
|
|
|
|
|
|
|
|
S |
1 |
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как векторы А1 А2 |
и А1 А3 : |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
а = |
А1 А2 |
= (3; – 6; – 4); |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
b = А1 А3 |
= (4; 1; 1), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b = А1 А2 А1 А3 = |
|
i |
j |
k |
|
= i |
|
6 4 |
|
– |
|
3 4 |
|
+ k |
|
3 6 |
|
= |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 6 4 |
|
|
|
j |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
4 |
|
1 |
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
4 |
1 |
|
|
|
4 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
– 19 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
= 2 i |
|
+ 27 k . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Значит, a b = (– 2; – 19; 27). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2)2 ( |
|
19)2 |
(27)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
b |
|
( |
|
|
|
|
1094 . |
|
|
|
|
|
|
||||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
1 |
|
|
1 |
|
|
|
|||
S |
|
a b |
1094 (ед. кв.). |
|||||||
|
|
|
|
|
||||||
А1 А2 А3 2 |
2 |
|||||||||
|
|
|
|
|
|
|||||
в) Объем пирамиды найдем по формуле
где а
Тогда
V 
|
|
|
|
|
|
1 |
|
|
|
1 |
а1 |
а2 |
а3 |
|
|
|
|
|
|
|
|
|
b1 |
b2 |
b3 |
, |
|||
|
|
|
|
V |
|
6 |
|
a b c |
|
6 |
||||
|
|
|
|
|
|
|
|
с1 |
с2 |
с3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= (а1; а2; а3), b = (b1; b2; b3), c = (с1; с2; с3) |
|
|
||||||||||||
Найдем координаты векторов А1 А2 , А1 А3 , А1 А4 : |
||||||||||||||
|
|
А1 А2 |
= (3; – 6; – 4), А1 А3 |
= (4; 1; 1), А1 А4 = (3; – 1; – 3). |
||||||||||
|
|
6 |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
1 |
4 |
1 |
1 |
11 |
(ед.куб.). |
|
|
|
|
|
||||
6 |
3 |
|
|
|
|
|
||||||||
3 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
Составим уравнение грани А1А2 А3 |
как уравнение плоскости, которая |
||||||||||||||||||||||
проходит через три точки М0(х0, у0, z0); М1(х1, у1, z1); М2(х2, у2, z2): |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
x0 |
y |
y0 |
z |
z0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x1 |
x0 y1 |
y0 z1 |
z0 |
|
= 0. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
x0 y2 |
y0 z2 |
|
z0 |
|
|
|
|
|
|||||||
|
|
Для точек А1, |
А2 |
, А3 имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
х 0 |
у 4 |
z 5 |
|
х 0 у 4 z 5 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 0 |
2 4 |
1 5 |
|
|
3 |
|
|
6 |
|
|
4 |
|
|
|
|
х ( 2) ( y 4) 19 (z 5) 27 |
|||||||||
|
4 |
0 |
5 |
4 |
6 |
5 |
|
|
4 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= – 2х – 19у + 76 +27z – 135 = – 2х – 19у ++27z – 59 = 0. |
||||||||||||||||||||||||||
|
|
Таким образом, |
2x 19 y |
27z |
59 |
|
0 – уравнение грани А1А2 А3 . |
|||||||||||||||||||
|
|
д) Из уравнения плоскости А1А2 А3 |
найдем нормальный вектор плоскости |
|||||||||||||||||||||||
n |
( 2; |
19; 27). Этот вектор является направляющим вектором для высоты, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
опущенной |
из |
точки |
|
А4 (3; 3; 2) |
на |
грань А1А2 А3 , т.е. l ( 2; 19; 27) . |
||||||||||||||||||||
Уравнение высоты имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
y |
3 |
|
|
z |
2 |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
13 |
|
|
|
|
27 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Длину высоты, опущенной из точки А4 |
на грань А1А2А3, найдем как |
|||||||||||||||||||||||
расстояние от точки А4 |
до плоскости А1А2А3 по формуле |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
d = |
|
Ax0 |
By0 |
Cz0 |
D |
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
A2 |
B2 |
|
C 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d = |
|
|
2) |
3 ( |
19) 3 |
27 |
2 |
59 |
|
= |
65 |
|
. |
|||||||
|
( |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( |
2)2 |
|
( 19)2 |
(27)2 |
|
|
1094 |
|||||||||||
Задание 11. Написать общее уравнение прямой на плоскости, проходящей через две точки А(2; – 1) и В (– 3;2).
РЕШЕНИЕ
Уравнение прямой на плоскости, проходящей через две точки, имеет вид:
y |
y1 |
= |
x |
x1 |
, |
|
|
|
|
||
y2 |
y1 |
|
x2 |
x1 |
|
где х1 и у1 – координаты одной из точек, а х2 и у2 –другой. В нашем случае это уравнение примет вид:
y |
( |
1) |
= |
|
|
x |
2 |
; |
|
2 |
( |
1) |
|
3 |
2 |
||||
|
|
|
|
||||||
|
y |
1 |
= |
x |
2 |
. |
|
||
|
3 |
|
|
5 |
|
||||
|
|
|
|
|
|
|
|
||
Отсюда, воспользовавшись свойством пропорции, получим:
– 5у – 5 = 3х – 6, 3х + 5у – 1 = 0 – общее уравнение прямой АВ.
Задание 12. Найти точку пересечения двух прямых на плоскости, заданных общими уравнениями:
l1: 2х – 3у – 1 = 0; l2: 3х + 2у – 8 = 0.
РЕШЕНИЕ
Для нахождения точки пересечения двух прямых нужно составить систему из их общих уравнений и решить ее относительно х и у. Полученные значения и будут координатами точки пересечения данных прямых. В нашем случае имеем:
2x 3y 1 0,
3x 2 y 8 0.
Для решения данной системы умножим первое уравнение системы на
(– 3), а второе на 2: |
|
|
|
6x |
9 y |
3 |
0, |
6x |
4 y |
16 |
0. |
Теперь сложим почленно первое и второе уравнения:
17

13у – 13 = 0.
Получили линейное уравнение, найдем из него у:
у = 1.
Чтобы найти х, подставим у = 1 в любое из исходных уравнений, например, во второе:
3х + 2∙1 – 8 = 0,
3х = 6, х = 2.
Таким образом, точка пересечения данных прямых имеет следующие координаты: (2; 1).
Задание 13. Написать уравнение прямой, проходящей через точку А(2; – 1) параллельно вектору l0 = (3; 4).
РЕШЕНИЕ
Уравнение прямой, проходящей через данную точку М0(х0; у0)
параллельно заданному вектору l0 |
= (т; п), имеет вид: |
||||||||||
|
|
x |
x0 |
|
= |
y |
y0 |
. |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
m |
|
|
|
n |
||||
В нашем случае получаем: |
|
|
|
|
|
|
|
|
|
||
|
x |
2 |
= |
|
y |
( 1) |
. |
||||
3 |
|
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
||||
Отсюда получаем:
4х – 8 = 3у + 3, 4х – 3у – 11 = 0 – искомое уравнение.
Задание 14. Написать уравнение прямой, проходящей через точку А(2; – 1) перпендикулярно вектору n = (3; 4).
РЕШЕНИЕ
Уравнение прямой, проходящей через данную точку М0(х0; у0), перпендикулярно заданному вектору n = (А; В), имеет вид:
А(х – х0) + В(у – у0) = 0.
В нашем случае получаем следующее уравнение:
3(х – 2) + 4(у – (– 1)) = 0, 3х – 6 + 4у + 4 = 0,
3х + 4у – 2 = 0 – искомое уравнение прямой.
Задание 15. Даны координаты точек: А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(– 4; 6; –3). Найти:
а) уравнение плоскости β, проходящей через точку С перпендикулярно вектору AB ;
18

б) канонические уравнения прямой l, проходящей через точку D перпендикулярно плоскости β.
РЕШЕНИЕ
а) Уравнение плоскости, проходящей через точку М0(х0; у0; z0) перпендикулярно вектору n = (А; В; С), имеет вид
А(х – х0) + В(у – у0) + С(z – z0) = 0.
Найдем координаты вектора AB = (2 – 1; 2 – 3; 1 – 6) = (1; – 1; – 5). Составим уравнение плоскости, проходящей через точку С(–1; 0; 1)
перпендикулярно вектору AB = (1; – 1; – 5):
1∙(х – (– 1)) + (– 1)∙(у – 0) + (– 5)∙(z – 1)= 0,
х+ 1 – у – 5z + 5 = 0,
х– у – 5z + 6 = 0 – уравнение плоскости β.
б) Из условия перпендикулярности прямой l и плоскости β следует, что в качестве направляющего вектора прямой s можно взять нормальный вектор n = (1; – 1; – 5) плоскости β. Тогда уравнение прямой l с учетом уравнения
x x0 |
= |
y y0 |
= |
z |
z0 |
, |
m |
n |
|
p |
|||
|
|
|
|
где х0, у0, z0 – координаты точки прямой; т, п, р – координаты направляющего вектора прямой, запишется в виде
x 40 |
= |
y 6 |
= |
z 3 |
. |
|
1 |
1 |
5 |
||||
|
|
|
Тема 2. Введение в математический анализ
1Находить область определения функции, заданной уравнением.
2Определять область значений функции, заданной уравнением.
3Вычислять пределы с применением основных теорем о пределах функций.
4 |
Раскрывать неопределенность вида |
|
|
и |
0 |
. |
|
|
0 |
||||||
|
|
|
|
|
|
|
|
5 |
Знать и применять формулы первого и второго замечательных |
||||||
пределов. |
|
|
|
|
|
|
|
6 |
Раскрывать неопределенность вида |
0 |
|
с помощью эквивалентных |
|||
|
|
|
|
||||
0 |
|
||||||
|
|
|
|
|
|||
бесконечно малых.
7Находить область непрерывности функции.
8Определять точки разрыва функции и их тип.
Задачи для самостоятельного решения
1 Найти область определения функций:
19

а) f (x) |
4 |
x2 ; |
|
|
|
|
||||
б) f (x) |
|
|
|
|
|
|
|
|
||
|
|
x 2 |
|
|
5 x; |
|||||
в) |
f (x) |
|
|
|
1 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
x2 |
5x |
|
|
|||||
|
|
|
|
|
|
|
|
|||
г) |
f (x) |
log 2 (2 x) |
2log x 5. |
|||||||
2Для функции у = 5х найти обратную функцию.
3Вычислить пределы:
а) |
lim (7x2 |
|
9x 1) ; |
б) lim |
2x2 |
x |
6 |
; |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
1 |
|
|
|
|
x |
2 x2 |
x |
6 |
|
|
|
|
|
|
|||||||||
|
|
|
sin 9x |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
в) |
lim |
; |
|
г) |
lim |
|
|
|
|
1 |
; |
|
|
|
|
|
|
||||||||
|
|
x |
|
|
|
|
|
|
|||||||||||||||||
|
x |
0 |
5x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4x |
7x2 |
|
|
|
|
|
|
x2 |
9x |
1 |
|
|
|
|
|
|||||||
д) |
lim |
|
|
; |
е) |
lim |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
7x2 |
|
|
|
|
|
|
|
|||||||||||||||
|
x |
0 |
sin 8x |
|
x |
|
2x |
5 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
4, |
x |
1; |
|
4 Исследовать на непрерывность функцию f (x) = |
x2 |
2, |
1 |
x 1; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x, |
x |
1. |
|||
5 Найти точки разрыва функции, выяснить их тип: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
f (x) |
|
|
x |
4 |
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Образцы решений
Задание 1. Вычислить пределы функций, не используя правило Лопиталя.
а) lim |
3x 2 |
4x 2 |
. |
|
|
|
|
8 |
x |
2 |
|
|
|
||
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Числитель и знаменатель дроби не имеют конечного предела при х |
, |
||||||
значит, выражение под знаком предела представляет собой при х |
|
||||||
неопределенность |
типа |
|
|
. Разделим числитель и знаменатель на |
х2 |
||
|
|
||||||
(наивысшую степень переменной х) и, на основании теорем о пределах, получим
20
