
metod_noi
.pdf
71
Фиг. 13
При вытаскивании конуса, вершиной будет пройден путь от z=0 до
z=H.
Найдем зависимость силы F(z). Пусть конус поднят над поверхностью жидкости на высоту z. Найдем зависимость силы F(z). На конус действуют:
|
ρ gπR2 H |
|
|
1) сила тяжести, равная |
1 |
и направленная вниз; 2)выталкивающая |
|
3 |
|||
|
|
сила жидкости, равная весу жидкости, вытесненной погруженной частью
конуса |
|
ρgπR2 H |
|
|
ρgπR2 z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
− |
|
|
|
, направленная вверх. |
|
|
|
|
|
|
|||||||||||||
3 |
|
3H 2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
При вытаскивании конуса сила F(z) должна уравновешивать сумму |
||||||||||||||||||||||||
этих сил. Следовательно F(z) = |
(ρ |
1 |
− ρ)gπR2 H |
+ |
ρgπR2 z3 |
. |
|
||||||||||||||||||
|
|
|
3 |
|
|
|
3H 2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
H |
|
|
|
H |
(ρ |
|
− |
ρ)gπR2 H |
|
ρgπR2 z3 |
|
|
||||||||||
Получаем A = ∫F(z)dz = ∫ |
1 |
|
|
|
|
|
|
+ |
|
|
|
|
dz = |
|
|
||||||||||
|
|
|
3 |
|
3H |
2 |
|
|
|
||||||||||||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(ρ |
− ρ)gπR2 Hz |
|
ρgπR2 z4 |
|
|
H |
|
|
(ρ − ρ)gπR2 H 2 |
|
ρgπR2 H 2 |
|
||||||||||||
|
|
|
|
||||||||||||||||||||||
= |
1 |
|
|
|
|
+ |
|
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
+ |
|
|
|
. |
|
3 |
|
|
12H 2 |
|
|
|
|
|
3 |
|
|
|
12 |
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определение работы, затрачиваемой на выкачивание жидкости из сосуда
К этому моменту мы предполагаем, что вы немного освоились с методом составления интегральных сумм, поэтому рассуждения станут менее подробными.
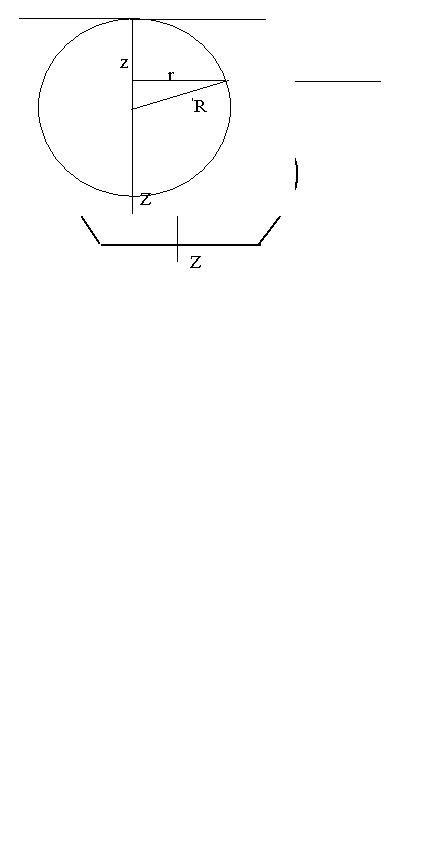
Пусть имеется сосуд глубины H, заполненный жидкостью с плотностью ρ (Фиг. 14). Будем считать, что ось Z направлена перпендикулярно поверхности жидкости, а начало оси находится на ее
72
поверхности. Предполагаем, что площадь сечения сосуда плоскостью, перпендикулярной оси Z, является известной функцией S(z). Требуется определить работу, которую необходимо затратить, чтобы выкачать воду из сосуда.
Фиг. 14.
В начале, определим работу A, которую необходимо затратить на выкачивания слоя толщины z , лежащего на глубине от z до z + z . Толщину слоя z считаем малой величиной. При выкачивании этот слой поднимется на высоту, приближенно равную z. Следовательно, работа A
оценивается величиной |
A ≈ |
Pz , где |
P - вес этого слоя. В свою очередь |
|
P = ρg V , где |
V - объем слоя. Объем указанного слоя приближенно |
|||
равен V ≈ S(z) |
z . Тогда |
A ≈ |
Pz ≈ ρgzS(z) z . Суммируя по всем слоям и |
|
переходя к пределу, получаем
h
A = ∫ρgzS(z)dz .
0
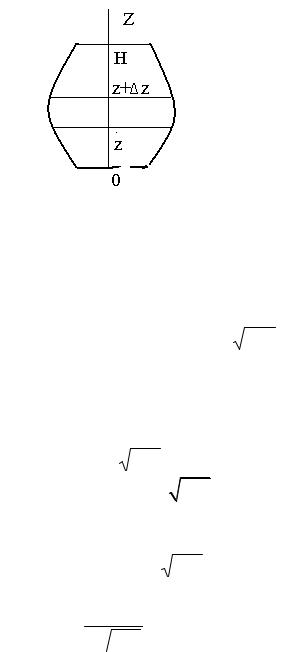
Задача 80. Определить работу, которую нужно затратить, чтобы выкачать жидкость плотности ρ из сосуда, имеющего форму сферы (Фиг. 15) радиуса R.
Фиг. 15.
73
Площадь сечения S(z) равна S(z)=πr 2 . По теореме Пифагора
|
|
|
|
|
|
|
|
|
|
2R |
r 2 = R2 − (R − z)2 = 2Rz − z2 . Следовательно A = ∫ρgzπ(2Rz − z2 )dz = |
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
3 |
z4 |
|
|
2R |
|
4 |
|
4 |
|
|
|
||||||||
|
|
Rz − |
|
|
|
|
= ρg |
|
πR |
|
|
|
|
|
|||||||
= ρgπ |
3 |
4 |
|
|
|
3 |
|
|||
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Определение времени вытекания жидкости из сосуда
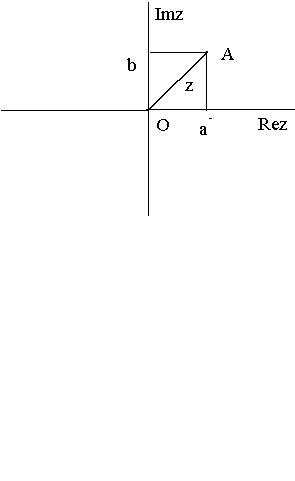
Постановка задачи. Имеется сосуд (Фиг. 16) глубины H, в дне которого имеется отверстие площади F . Требуется определить время вытекания жидкости из данного сосуда.
Фиг. 16.
Ось Z направим перпендикулярно свободной поверхности жидкости, а ее начало совместим с уровнем отверстия. Предположим, что площадь сечения сосуда плоскостью, перпендикулярной оси Z, является известной функцией S(z). Напомним, что скорость v вытекания жидкости из отверстия
вычисляется по формуле v = |
2gh , где h – уровень свободной поверхности |
||||||
жидкости над отверстием. |
|
|
|
||||
Оценим время |
t , за которое жидкость опустится с уровня z + z |
||||||
до уровня z . Объем жидкости в таком слое |
V оценивается соотношением |
||||||
V = S(z) z . Скорость вытекания жидкости |
v в этот момент оценивается |
||||||
величиной v = |
2gz . Объем |
V1 жидкости, вытекшей за время |
t примерно |
||||
равен V1 ≈ Fv |
t ≈ F |
2gz t . Из условия равенства V и V1 получаем |
|||||
оценку времени |
t , за которое жидкость опустится с уровня z + |
z |
|||||
до уровня z : |
t = |
S(z) z |
. |
|
|
|
|
|
|
|
|
||||
|
|
F |
2gz |
|
|
|
|
Тогда полное время t вытекания жидкости из сосуда равно
t = H∫ S(z)dz .
0 F  2gz
2gz
Задача 81. Найти время вытекания жидкости из цилиндрического сосуда радиуса R, высоты H, в дне которого имеется отверстие площади F .
|
|
|
|
|
|
|
|
|
|
74 |
|
Площадь сечения цилиндрического сосуда S(z) - постоянная величина |
|||||||||
равная |
- S(z) =πR2 . Тогда |
|
|
|
||||||
H |
πR2 dz |
|
πR2 |
|
H |
πR2 |
2H |
|
||
|
|
|
||||||||
t = ∫ |
|
|
= |
|
2 |
z |
= |
F |
g |
. |
F |
2gz |
|
||||||||
0 |
|
F 2g |
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
6.Комплексные числа
Валгебраической форме комплексное число z представляется в виде z = a + bi , где a - действительная часть, b - мнимая часть, число i - мнимая
единица, обладающая свойством i2 = −1.
→
Комплексное число удобно представлять вектором OA на комплексной плоскости (Фиг. 17).
Фиг. 17.
Два комплексных числа z1 = a + bi и z2 = c + di считаются равными тогда и
только тогда, когда равны их действительные и мнимые части. То есть z1 = z2 a = c, b = d .
Операции сложения (вычитания) для комплексных чисел определены следующим образом: z1 ± z2 = (a + bi) ± (c + di) = (a ± c) + (b ± d)i , то есть отдельно складываются (вычитаются) действительные и мнимые части. Комплексным нулем называется число вида 0= 0 + 0i . Нетрудно видеть, что для любого z выполнено z + 0 = z .
Операция умножения z1 z2 проводится по следующей схеме z1 z2 = (a + bi) (c + di) = a c + a di + b ci + b d i i
Так как i2 = −1, то
z1 z2 = (a + bi) (c + di) = a c + a di + b ci −b d = (ac −bd) + (ad + bc)i
Комплексной единицей называется число 1 =1 + 0i . Легко проверить, что для любого числа z выполнено 1 z = z .

75
Если комплексное число z равно z = a + bi , то комплексно сопряженным называется число, обозначаемое z , где z = a −bi . Заметим,
что zz = (a + bi)(a −bi) = a2 − (bi)2 = a2 + b2 .
Деление комплексных чисел осуществляется по следующей схеме (числитель и знаменатель умножают на сопряженное к знаменателю):
|
z1 |
= a + bi |
= |
(a + bi)(c − di) = (ac + bd ) + (bc − ad )i = ac + bd |
+ bc − ad i |
|
||||||||||||||||||||||||||||
|
z2 |
|
||||||||||||||||||||||||||||||||
|
c + di |
(c + di)(c − di) |
|
|
|
c2 + d 2 |
z1 |
|
|
|
|
c2 + d 2 |
c2 + d 2 |
|
||||||||||||||||||||
|
|
Задача 82. Вычислить z + z |
|
, z |
z |
|
, |
|
, если z = 2 −3i , z |
|
= 3 + 2i . |
|||||||||||||||||||||||
|
|
|
|
z2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
|
2 |
|
|
|
1 |
|
|
|
2 |
|
|
|
||||
|
|
Решение. z1 + z2 = (2 −3i) + (3 + 2i) = (2 + 3) + (−3 + 2)i =5 −i . |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
z1 z2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= (2 −3i) (3 + 2i) = 2 3 + 2 2i −3 3i −3 2 i i = 6 + 4i −9i + 6 =12 −5i |
||||||||||||||||||||||||||||||||
|
|
|
z1 |
= |
(2 −3i) |
= |
|
|
|
(2 −3i)(3 − 2i) |
= |
|
6 − 4i −9i − 6 |
= |
|
0 −13i |
= −i . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
(3 + 2i)(3 − 2i) |
|
|
13 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
z2 |
(3 + 2i) |
|
|
|
|
|
9 + 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Задача 83. Вычислить z + z |
|
, z |
z |
|
, |
z1 |
, если z =1 +5i , z |
|
|
= 5 − 2i |
||||||||||||||||||||||
|
|
|
|
z2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|||||
|
|
|
z1 + z2 = (1 + 5i) + (5 − 2i) = (1 + 5) + (5 − 2)i = 6 + 3i |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
z1 z2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= (1 + 5i) (5 − 2i) =1 5 −1 2i + 5 5i −5 2 i i =5 − 2i + 25i +10 =15 + 23i |
||||||||||||||||||||||||||||||||
|
|
|
z1 |
= |
(1 + 5i) |
= |
|
|
|
(1 + 5i)(5 + 2i) |
|
= |
|
5 + 2i + 25i −10 = −5 + 27i = − |
|
|
5 |
+ |
27 i |
|||||||||||||||
|
|
|
|
|
|
(5 − 2i)(5 + 2i) |
|
|
|
29 |
||||||||||||||||||||||||
|
|
|
z2 |
(5 − 2i) |
|
|
|
|
|
25 + 4 |
|
|
29 |
|
|
|
29 |
|||||||||||||||||
|
|
Тригонометрическая форма комплексного числа. |
|
|
|
|
|
|
||||||||||||||||||||||||||
Обозначим r |
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
a2 + b2 . Это число |
|
||||||||||||
- модуль вектора OA (Фиг. 16) r = |
|
|||||||||||||||||||||||||||||||||
назовем модулем |
|
z |
|
|
- комплексного числа z = a + bi . Заметим, что |
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
z =  z z .
z z .
→
Угол наклона вектора OA к действительной оси Rez обозначим ϕ и назовем аргументом комплексного числа z. Тогда a = r cosϕ , b = r sinϕ .
Следовательно, z = a + bi = r cosϕ + r sinϕ i = r(cosϕ + isinϕ) .
Представление комплексного числа в виде z = r(cosϕ + isinϕ)
называется тригонометрической формой комплексного числа. Заметим, что аргумент комплексного числа определен с точностью до слагаемого, кратного 2π . Если не будет специальных оговорок, мы будем предполагать, что речь идет о главном значении аргумента ϕ , где 0 ≤ϕ < 2π . В общем
случае два комплексных числа z1 = r1 (cosϕ1 + isinϕ1 ) и
z2 = r2 (cosϕ2 + isinϕ2 ) равны, когда равны их модули, а аргументы отличаются на слагаемое, кратное 2π .

76
Для комплексных чисел, заданных в тригонометрической форме, операции умножения и деления выполняются достаточно просто.
Пусть z1 = r1 (cosϕ1 + isinϕ1 ) , z2 = r2 (cosϕ2 + isinϕ2 ) .
Тогда:
z1 z2 = r1 (cosϕ1 + isinϕ1 ) r2 (cosϕ2 + isinϕ2 ) = r1r2 cos(ϕ1 +ϕ2 )+ isin (ϕ1 +ϕ2 )
( при умножении комплексных чисел модули перемножаются, а аргументы складываются);
z1 |
= |
r1 (cosϕ1 |
+ isinϕ1 ) |
= |
r1 |
cos(ϕ |
−ϕ |
|
)+ isin (ϕ |
−ϕ |
|
) |
||||||
|
|
|
r |
|
|
|||||||||||||
z |
2 |
|
r |
(cosϕ |
2 |
+ isinϕ |
2 |
) |
|
|
1 |
|
2 |
1 |
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
(при делении комплексных чисел модули делятся, а аргументы вычитаются). Из формулы умножения комплексных чисел, заданных в
тригонометрической форме следует, что если z = r(cosϕ + isinϕ) , то zn , где n – целое число равно
zn = r n (cos nϕ + isin nϕ)
Эта формула, называется формулой Муавра.
Если комплексное число задано в тригонометрической форме
z = r(cosϕ + isinϕ) , а нам требуется представить его в алгебраической форме
z = a + bi , то действительная и мнимая части комплексного числа определяются соотношениями a = r cosϕ, b = r sinϕ .
Если комплексное число представлено в алгебраической форме
z = a + bi , а нам требуется представить его в тригонометрической форме z = r(cosϕ + isinϕ) , то модуль и аргумент определяются соотношениями
r = a2 + b2 , cosϕ = |
a |
, sinϕ = |
b |
. Известные значения синуса и |
|
a2 + b2 |
a2 + b2 |
||||
|
|
|
косинуса однозначно определяют главное значение аргумента. Согласно формуле Эйлера eiϕ = cosϕ + isinϕ.
Следовательно, комплексное число z = r(cosϕ + isinϕ) может быть
записано в виде z = reiϕ .
Такое представление называется показательной формой комплексного числа.
Задача 84. Записать в тригонометрической и показательной форме z = 2 −i .
Имеем z = 2 −i . Следовательно a = 2, b = −1. Тогда:
r = a2 + b2 = 4 +1 = 5 ; cosϕ = |
a |
= |
2 |
, sinϕ = |
b |
= − |
1 |
, |
|
a2 + b2 |
5 |
a2 + b2 |
5 |
||||||
|
|
|
|
|
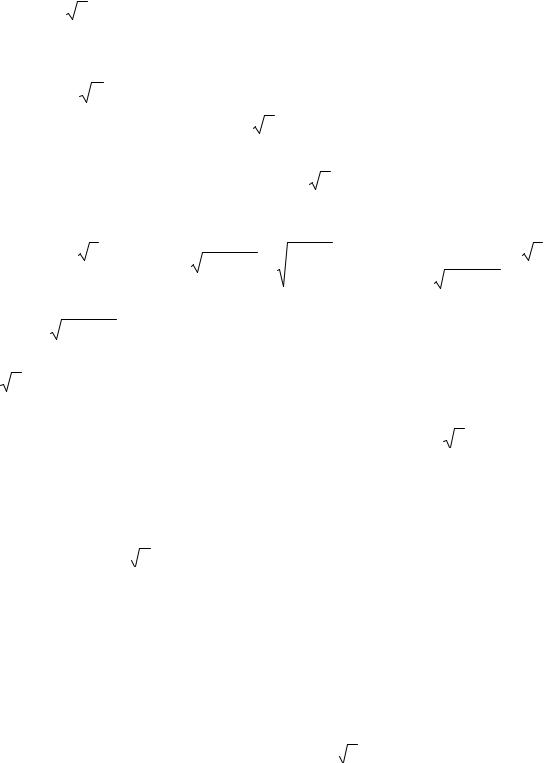
77
tgϕ = −12 . Так как действительная часть положительна, а мнимая отрицательна, то комплексное число находится в четвертой четверти
комплексной плоскости и, следовательно, ϕ = 2π − arctg |
1 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
Тогда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в тригонометрической форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
z = 2 −i = |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5 cos 2π − arctg |
|
|
+ isin 2π |
|
− arctg |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в показательной форме |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i 2π−arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z = 2 −i = 5e |
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
2006 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Задача 85. Вычислить: |
2 |
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Решение. Представим число z = |
|
|
|
3 |
+ |
1 |
i |
|
в тригонометрической |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
форме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||
Имеем a = |
|
3 |
, b = |
|
1 |
, |
r = a2 |
+ b2 |
= |
|
3 |
|
+ |
|
1 |
=1, |
cosϕ = |
|
|
|
|
= |
|
3 |
, |
|
|||||||||||||||||||||||||
2 |
2 |
|
4 |
|
4 |
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
|
||||||||||||||
sinϕ = |
|
|
|
b |
|
= |
1 . |
Тогда ϕ = π . Следовательно, согласно формуле |
|
||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Муавра |
2 + b2 |
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2006 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
1 |
|
|
|
|
π |
|
|
|
π 2006 |
|
|
|
2006 |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|||||||||||||||||||
|
|
+ |
|
|
|
|
= 1 cos |
|
+ isin |
|
|
|
=1 |
|
|
|
|
cos 2006 |
|
|
+ isin |
2006 |
|
|
= |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
i |
|
6 |
|
|
|
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
= cos 334π + |
|
+ isin |
334π |
+ |
|
|
= cos |
|
|
|
+ isin |
|
|
= |
|
+ |
|
|
|
i . |
|
|
|
|
|
|
|
||||||||||||||||||||||||
3 |
|
|
3 |
3 |
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Вычисление корня n -ой степени из комплексного числа |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
По определению n |
|
z |
называется число z , такое , что z n = z (n – целое |
|
|||||||||||||||||||||||||||||||||||||||||||||||
положительное число). |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Пусть в тригонометрической форме число z имеет вид |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
z = r(cosϕ + isinϕ) . Будем искать z1 |
в виде z1 = ρ(cosψ + isinψ) . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Поскольку z1n = z , то, согласно формуле Муавра r(cosϕ + isinϕ) = ρn (cos nψ + isin nψ ) .
Из условия равенства комплексных чисел, заданных в тригонометрической форме, следует:
1)равенство модулей r = ρn , то есть ρ = n r ;
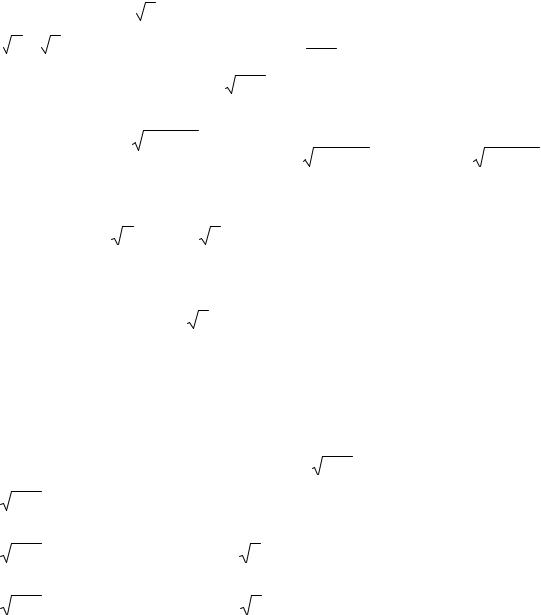
78
2)аргументы могут отличаться на слагаемое, кратное 2π , то есть nψ =ϕ + 2πk , где k – целое число.
Отметим, что в полученном выражении для аргумента ψ смысл имеют значения 0 ≤ k ≤ n −1. При дальнейшем увеличении k значения аргумента ψ будут отличаться от полученных ранее на величину, кратную 2π .
Следовательно, n z принимает n значений вида
n z = n r (cosψk + isinψk ) , где ψk = ϕn + 2πnk , 0 ≤ k ≤ n −1.
Задача 86. Вычислить 3 −8i .
Представим число z = −8i в тригонометрической форме. Имеем |
|
||||||||||||||||||||||||||||||||||||||||
a = 0, b = −8, |
|
r = |
|
|
|
a2 |
+ b2 |
=8 , |
cosϕ = |
|
|
a |
|
= 0 , |
sinϕ = |
|
b |
= −1. |
|||||||||||||||||||||||
|
|
|
a2 |
+ b2 |
|
a2 + b2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
3π |
|
|
|
|||||||||
Тогда ϕ = |
|
|
. Следовательно |
−8i =8 cos |
|
+ isin |
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
Будем искать 3 z |
|
|
в виде 3 z = ρ(cosψ + isinψ) . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Следовательно ρ |
3 |
(cos3ψ |
|
+ isin 3ψ) = |
|
|
|
|
3π |
|
|
|
|
3π |
|
|
|
||||||||||||||||||||||||
|
|
8 cos |
|
+ isin |
. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||||
Получаем ρ3 |
|
=8 ρ = 3 |
|
8 = 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3ψ = |
3π |
|
+ 2πk, 0 ≤ k ≤ 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем три значения аргумента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ψ1 = π + |
2π 0 |
= |
π |
, |
ψ2 = π + |
2π 1 |
= |
7π |
, ψ3 |
= π |
+ |
|
2π 2 |
= |
11π |
|
|||||||||||||||||||||||||
|
|
2 |
3 |
|
|
6 |
|
|
|||||||||||||||||||||||||||||||||
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
6 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
||||||||||
Следовательно, имеются три значения 3 |
−8i : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
−8i |
= |
|
|
|
|
π |
+ isin |
π |
= 2i ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
2 cos |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−8i |
|
|
|
|
|
|
7π |
+ isin |
7π |
|
|
3 −i ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
= |
2 cos |
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
−8i |
|
|
|
|
|
11π |
|
|
+ isin |
11π |
3 −i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
= |
2 cos |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
79
Литература
1.Я.С. Бугров, С.М. Никольский. Высшая математика т.2. Дифференциальное и интегральное исчисление. Дрофа. М. 2003. 510 с.
2.В.А. Ильин, А.В. Куркина. Высшая математика. Издательство МГУ. М. 2004. 594 с.
3.Н.С. Пискунов. Дифференциальное и интегральное исчисление.Т.1. М.
Наука. 2003.
4.Демидович Б.П. Задачи и упражнения по математическому анализу. М.
Астрель.2001.496 с.
5.И.П. Натансон. Краткий курс высшей математики. Изд. «Лань» М.2005.736с.
Содержание. |
|
Введение. |
3 |
1.Неопределенный интеграл |
3 |
2.Определенный интеграл |
39 |
3.Несобственный интеграл |
45 |
4.Геометрические приложения определенного интеграла |
56 |
5.Механические приложения определенного интеграла |
69 |
6.Комплексные числа |
74 |
Литература. |
79 |
