
metod_noi
.pdf
61
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
π |
|
|
|
|
9 |
∫2 (1 − cos2t − cos2 2t + cos3 2t)dt = |
9 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
9 |
∫2 |
|
|||||||||||||||||||||
= = |
t |
2 |
− |
|
sin 2t |
|
|
2 − |
(1 + cos4t) + |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
0 |
8 |
|
|
|
|
|
|
|
|
0 |
8 |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|||||
|
9 |
∫2 |
|
|
|
|
|
|
|
9π |
|
|
|
9 |
|
|
|
9 |
|
|
|
|
|
|
|
9 |
|
∫2 |
|
|
|
|
|||||||||
+ |
(1 −sin2 2t)cos2tdt = |
− |
t |
|
2 |
− |
sin 4t |
|
2 |
+ |
|
(1 −sin2 2t)d (sin 2t) = |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
4 |
0 |
|
|
|
|
|
|
|
8 |
8 |
|
|
0 |
|
32 |
|
|
|
|
|
0 |
|
8 |
|
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9π |
|
9π |
|
9 |
|
|
sin3 2t |
|
2 |
|
|
|
9π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
− |
|
+ |
|
|
− |
|
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8 |
16 |
8 |
sin 2t |
|
3 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
Задача 68. Найти площадь эллипса |
|
+ |
|
|
|
=1. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Эллипс с полуосями a, |
b (Фиг. 7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
- фигура, симметричная относительно |
|||||||||||||||||||||||||||||||||||||||||
всех координатных осей, поэтому достаточно найти площадь в первой координатной четверти.
Фиг. 7
Впервой четверти зададим эллипс параметрически x = a cost
y =bsin t
Тогда значению x = 0соответствует t = |
π |
, значению x = a соответствует |
|||||||
t = 0. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
Следовательно S = 4∫ydx = −4∫bsin t asin tdt =2ab ∫2 |
(1 − cos2t)dt = |
||||||||
|
|
|
|
|
0 |
π |
|
0 |
|
|
|
|
|
π |
|
2 |
|
|
|
|
sin 2t |
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
||
= 2ab t − |
|
|
|
|
=πab . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||

62
Рассмотрим задачу о вычислении площади криволинейного сектора.
Фиг. 8 Криволинейным сектором (фиг. 8) называется область, ограниченная
линиями, уравнения которых в полярной системе координат ( r,ϕ ) имеют вид:
1)два луча ϕ =α, ϕ = β (α < β) ; 2)линия r = f (ϕ) .
На фигуре 8 (предполагается, что ось X совпадает с полярной осью) лучу ϕ =α соответствует ОА (угол AOX равен α), лучу ϕ = β соответствует ОВ (угол ВOX равен β), линии r = f (ϕ) соответствует кривая АВ.
Разделим область на части лучами ϕ0 (ϕ0 =α) , ϕ1 ,…, ϕi (луч OCi ),
ϕi+1 (луч OCi+1 ),…, ϕn (ϕn = β) . Обозначим |
ϕi =ϕi+1 −ϕi . Площадь |
криволинейного сектора Ci+1OCi обозначим |
Si . |
Тогда полная площадь S криволинейного сектора ВОА может быть |
|
n−1 |
|
представлена в виде S = ∑ Si . |
|
i=0 |
|
Оценим значение Si , предполагая, что |
ϕi =ϕi+1 −ϕi - достаточно |
малая величина. Выберем значение угла ϕ =γi , где ϕi ≤γi ≤ϕi+1 (луч ODi ). Заменим криволинейный сектор Ci+1OCi круговым сектором радиуса ODi , где ODi = f (γ i) . При малом значении ϕi =ϕi+1 −ϕi есть все основания полагать, что их площади отличаются незначительно. Соответствующая
площадь кругового сектора радиуса OD равна |
1 |
f 2 (γ |
i |
) |
ϕ |
i |
. Тогда имеем |
|||
|
||||||||||
|
|
|
i |
2 |
|
|
|
|
||
n−1 |
n−1 |
1 f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S = ∑ |
Si ≈ ∑ |
(γi ) ϕ i . |
|
|
|
|
|
|
|
|
i=0 |
i=0 |
2 |
|
|
|
|
|
|
|
|
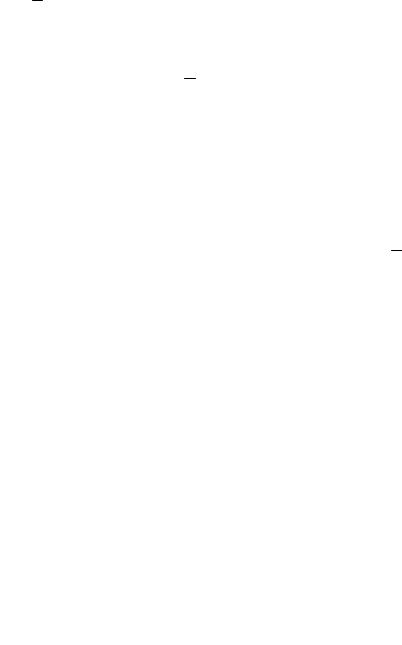
63
Полученная сумма является интегральной суммой для функции y = 12 f 2 (ϕ) на отрезке α ≤ϕ ≤ β . Переходя к пределу, при стремлении максимального значения ϕi к нулю, получаем
S = β∫1 f 2 (ϕ)dϕ.
α 2
Замечание.
Пусть область ограничена линиями, уравнения которых в полярной системе координат ( r,ϕ ) имеют вид:
1)два луча ϕ =α, ϕ = β (α < β) ;
2)линии r = f2 (ϕ), r = f1 (ϕ) , где f1(ϕ) ≤ f2 (ϕ) при α ≤ϕ ≤ β .
Тогда ее площадь вычисляется по формуле S = β∫1[f22 (ϕ) − f12 (ϕ)]dϕ
α 2
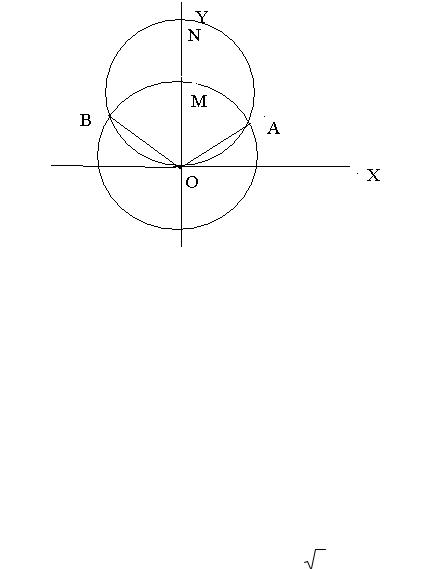
Задача 69. Найти площадь фигуры, ограниченной линией: r =sin 4ϕ.
Данная фигура схематично изображена на рисунке (Фиг. 9).
Фиг. 9.
Данный «цветок» состоит из четырех совершенно одинаковых «лепестков». (Напомним, что по смыслу полярной системы координат значение r ≥ 0 , поэтому для тех значений угла ϕ , при которых sin 4ϕ < 0 , точек на линии не существует). Поэтому достаточно найти площадь одного лепестка и умножить ее на четыре. «Первый лепесток» ограничен лучами
ϕ = 0 , ϕ = |
π |
и кривой r =sin 4ϕ. . Следовательно |
|
|
|
|
|
|||||||
π |
|
|
4 |
π |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
sin8ϕ |
|
π |
|
π |
|
|||
4 |
|
|
2 |
4 |
|
|
|
4 |
|
|
||||
S = 4∫ |
|
sin |
|
4ϕdϕ = ∫(1 |
− cos8ϕ)dϕ = |
ϕ − |
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|||||||||
0 |
2 |
|
|
|
0 |
|
|
8 |
|
0 |
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
64
Задача 70. Найти площадь фигуры, ограниченной линиями: r = 2sinϕ, r =1 (r ≥1).
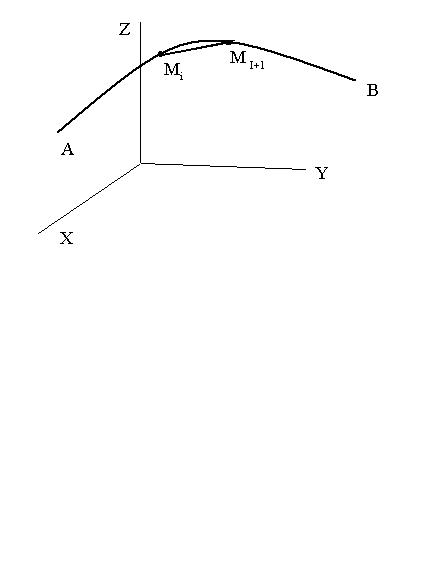
Данная фигура схематично изображена на рисунке (Фиг. 10).
Фиг. 10.
Она ограничена кривыми BNA и BMA . Найдем точки пересечения кривых r = 2sinϕ, r =1. Получаем 2sinϕ =1. На отрезке [0;2π] уравнение имеет два
корня ϕ 1 |
= π |
, ϕ |
2 = |
|
5π |
. Следовательно, в полярной системе координат луч |
|||||||||||||||||||||||
6 |
|||||||||||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5π |
|
|
|
|
|
||||
ОА имеет уравнение ϕ = π , луч ОВ - |
ϕ = |
, кривая BNA - r = 2sinϕ, |
|||||||||||||||||||||||||||
6 |
|||||||||||||||||||||||||||||
кривая BMA - r =1. |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
5π |
|
|
[4sin2 ϕ −1]dϕ = |
5π |
|
|
|
|
|
|
5π |
|
|||||||||
|
|
|
Тогда S = ∫6 |
1 |
∫6 |
1 [1 − 2cos2ϕ]dϕ = 1 |
|
|
|
|
|||||||||||||||||||
|
|
|
[ϕ −sin 2ϕ] |
6 |
= |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
2 |
|
|
|
|
|
|
|
π |
2 |
|
|
2 |
|
π |
|
||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
|
5π |
−sin |
5π |
|
|
1 |
|
π |
−sin |
π |
|
π |
|
|
|
3 |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
− |
|
|
|
|
= |
|
+ |
|
|
|
|
|
|
|
|
|||||||||
2 |
6 |
|
2 |
|
3 |
3 |
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вычисление объема тела по известным площадям параллельных сечений.
Пусть имеется некоторое тело в пространстве. Обозначим Q(z) -
площади его сечений плоскостями, перпендикулярными оси Z. Требуется определить объем тела.
Будем предполагать, что плоскости пересекают данное тело при значениях z, лежащих на отрезке [a;b]. Разобьем отрезок [a;b] на n частей

|
65 |
|
точками z0 |
( z0 =a), z1, …, zi , zi+1,…, zn |
( zn =b). Обозначим: zi = zi+1 − zi , |
Vi - объем слоя толщины zi , заключенного между сечениями z= zi и |
||
z= zi+1. Если |
zi достаточно мало, то приближенно этот объем можно |
|
оценить как объем цилиндра высоты zi |
и площади основания Q(ci ) , где |
|
zi ≤ ci |
≤ zi+1 , то есть Vi ≈Q(ci ) zi . |
Тогда полный объем V приближенно равен |
|
n−1 |
n−1 |
V ≈ ∑ |
Vi =∑Q(ci ) zi . |
i=0 |
i=0 |
Полученная сумма является интегральной суммой для функции Q(z) на отрезке [a;b]. Окончательная формула для объема имеет вид
b
V = ∫Q(z)dz
a
Замечание. В частности, если тело получено вращением относительно оси X криволинейной трапеции, ограниченной линиями: x = a, x =b ,
|
y = f1(x), |
y = f2 (x) , где 0 ≤ f1 (x) ≤ f2 (x) при a ≤ x ≤b , то площадь сечения |
|
||||||||||||||||||||||||||||||||||
равна Q(x)=π[f2 |
2 (x) − f12 (x)] |
и объем соответственно равен |
|
|
|
|
|||||||||||||||||||||||||||||||
V =π∫b [f22 (x) − f12 (x)]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
. |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
|
z2 |
|
|
|
|
|
|
|||||
|
|
|
|
Задача 71. Найти объем эллипсоида |
|
+ |
|
|
+ |
=1. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Рассмотрим сечения данного эллипсоида плоскостями, |
|
|
|
|
|||||||||||||||||||||||||||||
перпендикулярными оси Z. Преобразуем уравнение эллипсоида |
|
|
|
||||||||||||||||||||||||||||||||||
|
x2 |
+ |
|
y2 |
|
+ |
z2 |
=1 |
|
x2 |
+ |
y2 |
= |
1 − |
z2 |
|
|
x2 |
|
|
|
|
|
|
+ |
|
|
y2 |
|
|
=1. |
|
|
||||
|
a2 |
|
b2 |
c2 |
a2 |
b2 |
c2 |
|
|
|
z2 |
2 |
|
|
|
z2 |
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 1 |
− |
|
|
|
|
|
|
b |
1 − |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
c2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, сечением эллипсоида является эллипс с полуосями a 1− |
z2 |
, |
|||||||||||||||||||||||||||||||||||
c2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b 1 − |
|
z2 |
. Как было показано ранее, площадь эллипса с полуосями a,b равна |
||||||||||||||||||||||||||||||||||
|
c2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
πab . Следовательно площадь сечения эллипсоида Q(z) выражается формулой
|
|
z2 |
|
|
|
|
− |
|
|
|
, где − c ≤ z ≤ c . |
|
2 |
||||
Q(z) =πab 1 |
c |
|
|||
|
|
|
|
|
|
c |
|
|
z |
2 |
|
|
z |
3 |
|
|
c |
|
4 |
|
|
|
|
|
|
||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
= |
πabc . |
|||
|
|
2 |
|
|
2 |
|
|||||||||
Тогда V = ∫πab 1 |
c |
dz =πab z − |
3c |
|
|
|
3 |
||||||||
−c |
|
|
|
|
|
|
|
|
−c |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
66
Задача 72. Найти объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями.
y = cos1 x ; y = 0; x = 0; x = π4 .
π |
|
|
|
|
|
4 |
1 |
|
|
π |
|
Решение. V =π ∫0 |
dx =πtgx |
|
04 |
||
|
|||||
cos2 x |
|||||
|
=π .
Вычисление длин кривых.
Предположим, что в пространстве (X,Y,Z) параметрически задана
x =ϕ(t)
кривая y =ψ(t) . Требуется определить длину дуги данной кривой, если
z = χ(t)
значения параметра t при этом изменяются на отрезке [a;b] (дуга АВ на фиг. 11).
Фиг. 11.
Относительно функций ϕ(t),ψ(t), χ(t) будем предполагать, что они являются непрерывными и имеют непрерывные производные на отрезке [a;b].
Разобьем отрезок [a;b] |
на n частей точками t0 |
(t0 =a), t1 , …, ti , ti+1 ,…, tn |
|||
(tn =b). Обозначим: |
ti |
=ti+1 −ti , |
si - длина дуги M i M i+1 , где координаты |
||
точек соответственно равны M i (ϕ(ti );ψ(ti ); χ(ti )), |
|||||
M i+1(ϕ(ti+1);ψ(ti+1); χ(ti+1)). Если |
ti достаточно мало, то приближенно si - |
||||
длину дуги M i M i+1 |
можно заменить величиной |
li - длиной секущей |
|||
M i M i+1 . |
|
→ |
|
|
|
|
|
|
zi }, где |
|
|
Рассмотрим вектор |
M i M i+1 ={ xi ; |
yi ; |
|
||
xi =ϕ(ti+1) −ϕ(ti ) , |
yi =ψ(ti+1) −ψ(ti ) , |
zi = χ(ti+1) − χ(ti ) . |
|||
|
|
|
|
→ |
|
Значение li равно модулю вектора M i M i+1 , то есть

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
l |
i |
= x |
2 + y |
2 |
+ z 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
i |
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Согласно теореме Лагранжа |
|
|
|
|
|
|
|
|||||||||||
xi =ϕ(ti+1) −ϕ(ti ) =ϕ′(τ1i ) ti , |
yi =ψ(ti+1 ) −ψ(ti ) =ψ′(τ2i ) ti , |
|||||||||||||||||||
zi |
= χ(ti+1) − χ(ti ) = χ′(τ3i ) ti , где точки τ1i ,τ2i ,τ3i лежат на отрезке [ti , ti+1 ]. |
|||||||||||||||||||
|
|
Тогда L - длина дуги АВ приближенно равна |
||||||||||||||||||
|
|
n−1 |
[ |
|
|
1i |
|
] |
[ |
|
2i ] |
|
|
[ |
|
|
3i |
|
] |
i |
|
|
∑ i |
′ |
|
|
′ |
2 |
|
′ |
|
|
|||||||||
L ≈ |
l ≈ ϕ |
|
|
) |
2 |
+ ψ |
|
+ |
|
|
|
) |
2 |
t . |
||||||
(τ |
|
|
|
(τ ) |
|
|
χ (τ |
|
|
|||||||||||
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная сумма не является интегральной суммой, поскольку точки |
||||||||||||||||||||
τ1i ,τ2i ,τ3i |
не обязаны совпадать. Однако, поскольку τ1i ,τ2i ,τ3i лежат на |
|||||||||||||||||||
отрезке длиной ti , то можно показать, что ее предел при стремлении к |
||||||||||||||||||||
нулю максимального значения |
|
ti |
равен пределу интегральной суммы для |
|||||||||||||||||
функции |
′ |
|
2 |
+[ψ |
′ |
2 |
′ |
|
2 |
на отрезке [a;b] . |
||||||||||
[ϕ (t)] |
(t)] |
[χ (t)] |
||||||||||||||||||
Следовательно |
L = ∫b |
[ϕ′(t)]2 +[ψ′(t)]2 +[χ′(t)]2 dt . |
||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
С точки зрения математики вопрос о длине кривой, это не совсем простой вопрос. Фактически мы определяем длину кривой, как предел длин секущих и показываем, что этот предел равен полученному определенному интегралу.
Замечание 1. Если кривая задана параметрически на плоскости
x =ϕ(t)
y =ψ(t)
L = ∫b |
[ϕ′(t)]2 +[ψ′(t)]2 dt . |
a |
|
Замечание 2. Если кривая на плоскости задана уравнением y = f (x) ,
где a ≤ x ≤b , то можно считать, что роль параметра t играет независимая переменная x . Тогда длина кривой вычисляется по формуле
b |
′ |
2 |
|
L = ∫ |
|||
1 +[f (x)] dx . |
|||
a
Задача 73. Найти длину кривой, заданной уравнением: y = 12 (ex + e−x ), 0 ≤ x ≤1.
|
|
|
1 |
|
′ |
2 |
1 |
ex |
− e−x |
2 |
1 |
e2x + 2 + e−2x |
dx = |
||||||||
Решение. L = ∫ |
1 +[f (x)] |
dx = ∫ |
1 + |
2 |
|
dx = ∫ |
|
|
4 |
||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||||
1 |
ex + e−x |
2 |
1 ex + e−x |
ex − e−x |
|
1 |
e − e−1 |
|
e2 −1 |
|
|
||||||||||
|
|
|
|
||||||||||||||||||
= ∫ |
|
|
|
dx = ∫ |
|
|
|
dx = |
|
|
|
|
= |
|
|
= |
|
|
. |
|
|
2 |
|
2 |
|
2 |
|
|
2 |
2e |
|
||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 74. Найти длину кривой, заданной уравнениями:
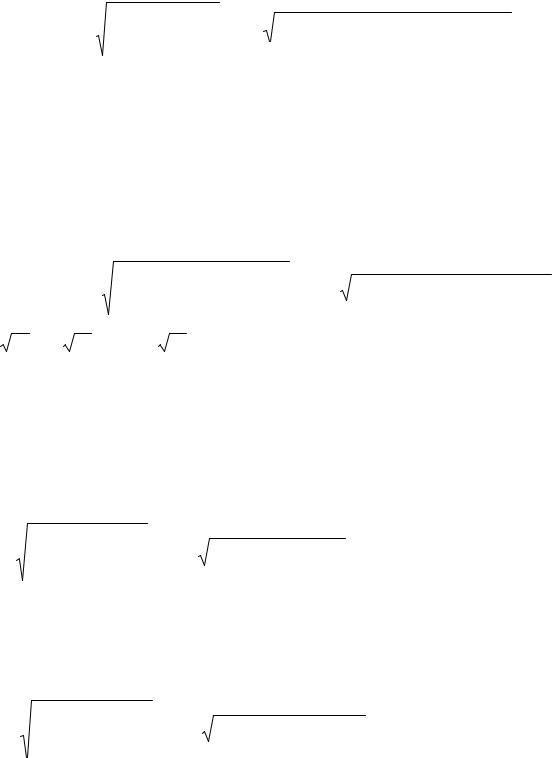
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
t, |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 2sin |
|
|
|
0 ≤ t ≤ |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y = 2cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
π |
|
|
|
2 |
dy 2 |
|
|
π |
|
[6sin |
|
|
|
|
+ [− 6cos |
|
|
|
|||
|
2 |
dx |
|
|
2 |
|
2 |
|
2 |
2 |
2 |
dt = |
||||||||||
Решение. L = ∫ |
|
|
|
|
+ |
dt = ∫ |
|
|
t cost] |
|
t sin t] |
|||||||||||
|
0 |
dt |
|
dt |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
π |
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
= ∫2 |
6sint costdt =3∫2 sin 2tdt = − |
3 cos2t |
|
|
3 cosπ |
|
3 cos0 =3 . |
|
||||||||||||||
|
2 |
= − |
+ |
|
||||||||||||||||||
0 |
|
0 |
|
|
|
|
|
2 |
|
|
|
0 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Задача 75. Найти длину кривой, заданной уравнениями: |
|
||||||||||||||||||||
|
x = 2cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 ≤t ≤ 2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y = 2sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z =3t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
dx 2 |
dy |
|
2 |
dz |
2 |
|
2π |
|
|
2 |
|
2 |
2 |
|||||||
Решение. L = ∫ |
|
|
|
|
|
+ |
|
+ |
|
|
dt = |
∫ |
[− 2sin t] +[2cost] |
+[3] dt = |
||||||||
|
0 |
dt |
dt |
|
|
dt |
|
|
0 |
|
|
|
|
|
|
|||||||
2π |
2π = 2π 13 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ∫ 13dt = 13t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Если кривая задана уравнением в полярной системе координат r = f (ϕ) , где α ≤ϕ ≤ β , то, поскольку x = r cosϕ, y = r sinϕ , ее
x = f (ϕ)cosϕ
можно рассматривать как заданную параметрически ,
y = f (ϕ)sinϕ
где роль параметра играет угол φ (α ≤ϕ ≤ β ). Тогда длина кривой вычисляется по формуле
β |
dx 2 |
dy |
2 |
β |
2 |
′ |
2 |
||||
L = ∫ |
|
|
|
+ |
|
|
|
dϕ = ∫ |
[f (ϕ)] |
+[f (ϕ)] dϕ . |
|
|
|
|
|||||||||
α |
dϕ |
dϕ |
|
α |
|
|
|
||||
Задача 76. Найти длину кривой, заданной уравнением r = 4sinϕ, где
0 ≤ϕ ≤π .
Решение.
π |
dx 2 |
dy 2 |
π |
2 |
2 |
π |
||||
L = ∫ |
|
|
|
+ |
|
|
dϕ = ∫ |
[4sinϕ] |
+[4cosϕ] |
dϕ = ∫4dϕ = 4π |
|
|
|||||||||
0 |
dϕ |
dϕ |
0 |
|
|
0 |
||||
69
5. Механические приложения определенного интеграла
Вычисление силы давления жидкости на вертикально погруженную в нее пластину
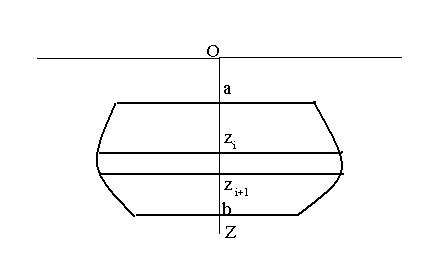
Пусть имеется пластина, вертикально погруженная в жидкость (Фиг. 12). Будем предполагать, что ось Z перпендикулярна свободной поверхности жидкости, а ее начало совпадает со свободной поверхностью. Верхний край пластины находится на глубине z = a , нижний на глубине
z =b . Пусть ширина пластины l в направлении, перпендикулярном оси Z, - переменная, являющаяся известной функцией l =l(z) . Плотность жидкости
обозначим ρ . Требуется определить силу давления жидкости на пластину. (Напомним из курса физики, что давление p на глубине z равно p = ρ g z ,
где g =9,81 м/ сек2 - ускорение свободного падения.)
Фиг. 12
Разделим пластину на n частей прямыми, параллельными свободной поверхности: z = z0 (z0 = a) , z = z1 , …, z = zi , z = zi+1 ,…., z = zn (zn =b) .
Обозначим zi = zi+1 − zi .
Оценим Fi - значение силы, действующей на часть пластины, лежащую между прямыми z = zi и z = zi+1 .
Если zi = zi+1 − zi достаточно мало, то давление pi на таком узком слое можно приближенно считать постоянным и принять равным pi ≈ ρgzi .
Сам слой можно приближенно считать прямоугольным, |
а его площадь Si |
|
принять равной |
Si ≈l(zi ) zi . Тогда значение силы Fi |
можно выразить |
соотношением |
Fi ≈ pi Si ≈ ρgzil(zi ) zi . |
|
Следовательно, суммарная сила F, действующая на пластину
n−1
приближенно равна F ≈ ∑ρgzil(zi ) zi . Полученная сумма является
i=0
интегральной суммой для функции ρ g z l(z) на отрезке a ≤ z ≤b .

70
b
Окончательно получаем F = ∫ρ g z l(z)dz .
a
Задача 78. Найти силу давления жидкости плотности ρ на
вертикально погруженную в нее пластину, имеющую форму трапеции с верхним основанием а, нижним основанием b, высотой h, если верхнее основание находится на поверхности воды.
Поскольку пластина имеет форму трапеции, то ее ширина l(z) является линейной функцией z вида l(z) = kz + c . Так как l(0) = a , l(h) =b , то
l(z) = b −h a z + a .
Следовательно
h |
b − a |
|
b − a |
|
3 |
|
z2 |
|
h |
(2b + a)h2 |
|
|||
|
|
|
|
|||||||||||
F = ∫ρgz |
h |
z + a dz = ρg |
3h |
z |
|
+ a |
|
|
|
= ρg |
|
. |
||
|
2 |
6 |
||||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Вычисление работы переменной силы
Пусть переменная сила F(x) перемещает точку по прямой из положения x=a в положение x=b. Требуется определить работу, совершенную данной силой. Разобьем весь путь из положения x=a в положение x=b на n частей
точками x0 |
(x0 = a) , x1 , …, xi , xi+1 ,…., xn (zn =b) . Обозначим |
xi = xi+1 − xi . |
|
Работу по перемещению из положения xi в xi+1 обозначим Ai . Если |
|
xi = xi+1 − xi |
достаточно малая величина, то силу при перемещении из |
положения xi |
в xi+1 можно приближенно считать постоянной и равной |
F(xi ) . Тогда значение Ai ≈ F (xi ) xi . Тогда полная работа A приближенно
n−1
равна - A ≈ ∑F (xi ) xi .
i=0
Полученная сумма является интегральной суммой для функции F(x) на отрезке [a;b]. Следовательно, выражение для работы может быть записано в
b
виде A = ∫F (x)dx .
a
Задача 79. Найти работу, которую нужно затратить, чтобы вытащить из жидкости плотности ρ конус радиуса R, высоты H, плотности ρ1 , если в
начальный момент вершина конуса находится на поверхности, а плоскость основания параллельна поверхности жидкости.
Решение. Ось Z направим перпендикулярно поверхности жидкости, а ее начало поместим на ее поверхности (Фиг. 13).
