
8.6 Меры сложности алгоритмов. Классы задач р, ехр и np. Np полные задачи
Хотя теория алгоритмов развивается только несколько десятков лет, а решением задач человечество занималось всегда, задача, как математический объект представляется более загадочной, чем алгоритм.
Одну и ту же задачу могут решать много алгоритмов. Эффективность работы каждого из них описывается разнообразными характеристиками.
При анализе алгоритма определяется количество "времени", необходимое для его выполнения. Это не реальное число секунд или других промежутков времени, а приблизительное число операций, выполняемых алгоритмом. Число операций и измеряет относительное время выполнения алгоритма. Таким образом, иногда мы будем называть "временем" вычислительную сложность алгоритма. Фактически количество секунд, требуемое для выполнения алгоритма на компьютере непригодно для анализа, поскольку нас интересует только относительная эффективность алгоритма, решающего конкретную задачу. Действительно алгоритм не становится лучше, если его перенести на более быстрый компьютер, или хуже, если его исполнять на более медленном компьютере.
Во-вторых, фактическое количество операций алгоритма на тех или иных вводимых данных не предоставляет большого интереса и мало его характеризует. Вместо этого важной характеристикой является зависимость числа операций конкретного алгоритма от размера входных данных. Мы можем сравнить два алгоритма по скорости роста числа операций от роста входных данных. Именно скорость роста играет ключевую роль.
При анализе алгоритмов учитывается сложность алгоритмов по времени, однако нужно учитывать и то, сколько памяти нужно тому или иному алгоритму. На ранних этапах развития компьютеров этот анализ носил принципиальный характер. Нередко приходилось выбирать более медленный алгоритм, если он требовал меньше памяти. Разработчики современных программ не ощущают потребность в экономии памяти, в результате чего компьютер морально устаревает задолго до их физической негодности.
Скоростью роста алгоритма называется скорость роста числа операций при возрастании объёма входных данных. Нас интересует только общий характер поведения алгоритма, а не подробности этого поведения. Подводя итоги, при анализе алгоритмов нас будет интересовать скорее класс скорости роста, к которому относится алгоритм, нежели точное количество выполняемых им операций аддитивного и мультикативного типа.
Некоторые часто встречающиеся классы функций приведены в таблице. В этой таблице приведены значения функций из данного класса на широком диапазоне значений аргумента. Видно, что при небольших размерах входных данных значения функций отличаются незначительно, однако при росте этих размеров разница существенно возрастает. Во-вторых, быстродействующие функции доминируют над функциями с более медленным ростом. Поэтому если мы обнаружим, что сложность алгоритма представляет собой сумму двух или нескольких таких функций, то будем часто отбрасывать все функции кроме тех, которые растут быстрее всего. Если, например, установлено, что алгоритму нужно х3-30х операций, то будем считать, что сложность алгоритма растёт как х3. Причина этого в том, что уже при 100 входных данных разница между х3 и х3 -30х составляет лишь 0,3%.
Таблица классов роста функций
|
n |
log2n |
n2 |
n3 |
2n |
n! |
|
1 |
0 |
1 |
1 |
2 |
1 |
|
2 |
1 |
4 |
8 |
4 |
2 |
|
5 |
2.3 |
25 |
125 |
32 |
120 |
|
10 |
3.3 |
100 |
1000 |
1024 |
362880 |
|
15 |
3.9 |
225 |
3375 |
32768 |
1,307*1012 |
|
20 |
4.3 |
400 |
8000 |
1048576 |
2,432*1018 |
|
30 |
4.9 |
900 |
27000 |
1073741824 |
2,652*1032 |
Скорость роста сложности алгоритма играет важную роль, скорость роста определяется старшим, доминирующим членом формулы. Отбросив все младшие члены, мы получаем то, что называется порядком функции или алгоритма, скоростью роста сложности которого она является. Алгоритмы можно сгруппировать по скорости роста их сложностей.
Справедливо отметив, что для любой разрешимой задачи существует множество различных алгоритмов, ее решающих, предположим, что сложность самого простого из таких алгоритмов можно считать сложностью задачи.Процесс поиска для данной задачи алгоритма минимальной сложности был назван оптимизацией алгоритма. К сожалению, в большинстве случаев этот процесс не удается довести до конца и вместо оптимизации получаем лишь некоторое улучшение. Поэтому оценивать сложность задачи через анализ текста оптимального алгоритма обычно не возможно, а другого способа у нас пока нет.
Компьютерные науки делают пока только первые шаги в классификации задач по сложности. Естественно, что начинаем с дихотомии: попытки разделить все задачи на два класса – легкие и трудные. Границу между ними можно проводить по-разному, но все сошлись во мнении, что задачи, для решения которых требуется выполнить O(n), O(n2), O(n3), … операций – это легкие задачи (здесь n –параметр сложности исходных данных). Задачи же с оценкой сложности 0(2n) и более — сложные. Первую группу задач называют задачами полиномиальной сложности, поскольку их временная сложность ограничивается сверху некоторым полиномом (быть может, очень большой, но конечной степени п). Обозначим множество таких задач Р. Вторую группу называют задачами экспоненциальной сложности, поскольку в общем случае (т. е. для исходных данных, наиболее «неудобных» для любого из алгоритмов, решающих задачу) требуется количество операций, увеличивающееся с ростом п по крайней мере экспоненциально. Обозначим множество этих задач ЕХР.
Такое разграничение практически оправдано. Представим себе, что на самом быстром из доступных нам компьютеров решаем две задачи, полиномиальную Р1 с параметром сложности исходных данных n1 и экспоненциальную Р2 с параметром n2. Эти две задачи решаются примерно одинаковое время Т и находятся на грани того, чтобы испытывать наше терпение: согласны ждать время Т, но ни секунды больше! И вот, наконец, мы получили новый компьютер, работающий в несколько (k) раз быстрее, чем старый. Вопрос: насколько более сложные задачи можно решать на новом компьютере (как изменятся n1 и n2 ?), если наши возможности ожидания решения не изменились ?
Простой анализ показывает, что доступная сложность полиномиальной задачи увеличилась в несколько РАЗ, стала равной m*n1, а доступная сложность экспоненциальной задачи увеличилась НА несколько ЕДИНИЦ, стала равной п2 + l. Здесь m и l вычисляются через k. Например, если первая задача имеет линейную сложность, а вторая — 2n, то ускорение компьютера в два раза (k = 2) приводит к значениям 2n1, и n2 + 1. Это действительно качественно различные результаты.
Известны многие представители класса задач полиномиальной сложности: вычисление скалярного произведения векторов, произведение матриц, решение системы линейных уравнений, сортировка массива чисел, вычисление наибольшего общего делителя, вычисление факториала, ... Хотелось бы, чтобы все задачи были легкими, но сегодня для ряда задач известны только экспоненциальные алгоритмы! В связи с попыткой классификации сразу возникает много вопросов. Существуют ли неполиномиальные задачи или для любой задачи может быть построен полиномиальный алгоритм? Если существуют, то где проходит граница между полиномиальными и неполиномиальными задачами, как ее описать (иными словами, найти легко вычислимую характеристическую функцию множества Р)?
Изобразим условно взаимоотношение классов задач полиномиальной и экспоненциальной сложностей (рис. 8.3).
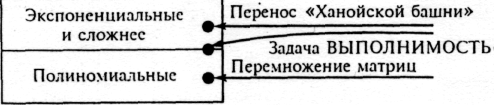
Рис. 8.3. Сложность некоторых задач
Здесь каждая точка области, ограниченной прямоугольником, представляет некоторую задачу. Две точки — это примеры задач из разных классов. Выше было выяснено, что для переноса «Ханойской башни» требуется 0(2n) операций, а для перемножения матриц не более, чем 0(n3) операций. О третьей точке — задаче ВЫПОЛНИМОСТЬ — речь пойдет ниже.
Где проходит граница между классами задач полиномиальной сложности Р и экспоненциальной сложности ЕХР ? Ответ на этот вопрос, т. е. описание границы (например, задачи с такими-то свойствами входят в класс Р, а все остальные входят в класс ЕХР) в настоящее время не известен. Чтобы разведать границу, математики придумали еще один класс задач — NP. Интуитивно предполагается, что он может оказаться «нарушителем границы». Это класс задач, которые можно решить за полиномиальное время (Р), но на машине, более мощной, чем обычная однопроцессорная машина — на недетерминированном (N) вычислителе. Недетерминированный вычислитель исполняет так называемые недетерминированные алгоритмы. Напомним свойство детерминированности определенность (детерминированность) алгоритма означает, что для каждого шага могут быть по набору исходных для шага данных однозначно вычислены результаты выполнения шага и эти результаты не зависят ни от каких случайных факторов. Соответственно этому и алгоритм в целом по окончании работы исполнителя выдает вполне определенный результат.
Недетерминированный алгоритм лишен этого свойства. Разрешаем шаги с неоднозначным результатом — шаги, вырабатывающие сразу несколько значений для одной и той же переменной. Эти несколько значений далее могут быть использованы одним из двух способов.
Первый способ. Создать несколько параллельно выполняющихся процессов (по процессу для каждого значения) для продолжения вычислений. Это возможно на многопроцессорной машине с неограниченно большим количеством параллельно работающих процессоров.
Второй способ. Угадать, какое из нескольких значений, полученных на данном шаге, является правильным (задающим искомое решение) и использовать в дальнейшем только его, игнорируя все остальные. В этом случае требуется только один процессор, но дополненный угадывающим устройством.
С точки зрения теории сложности не важно, каким именно из двух способов производить вычисление (временная сложность одинакова). Первый способ соответствует дереву возможностей и параллельному движению по всем ветвям дерева, а второй способ состоит в угадывании того, по какой ветви нужно двигаться и в движении по угаданной ветви.
Задача о переносе «Ханойской башни» по самой постановке не может быть распараллелена, так как в один момент времени только один диск переносится с иглы на иглу. Поэтому, даже при появлении такой мощной техники как недетерминированные машины эта задача остается в классе ЕХР.
Задача, решаемая за полиномиальное время на обычной машине, может быть решена за полиномиальное время и на недетерминированной машине, т. е.
P NP.
Верно ли обратное (и тогда Р = NP) или существуют задачи, решаемые за полиномиальное время на недетерминированной машине, но требующие экспоненциального времени на однопроцессорной машине (тогда Р NP, NP \ Р ) ?
В первом случае ничего нового в классификации задач от введения класса NP не получим. Но появляется много надежд. Дело в том, что для некоторых задач из класса NP известны только экспоненциальные алгоритмы для их решения на однопроцессорной машине. Если Р = NP, т. е. надежда разработать и полиномиальные алгоритмы. Вопрос этот не праздный. На карту поставлено не только машинное время. В криптографии (науке о шифровании информации) существует целое направление — шифрование с открытым ключом. В его основе использование математических задач, решаемых алгоритмами экспоненциальной сложности. Если вдруг для них найдутся эффективные полиномиальные алгоритмы, то многие секреты перестанут быть секретами.
Но и во втором случае появляется много вопросов. Что собой представляет класс NP \ Р ? Чем задачи из этого класса отличаются от других задач из ЕХР? В настоящее время развита довольно большая теория задач класса NP в предположении, что NP Р. Кому-то может показаться, что это сродни теории привидений. Не известно, есть ли привидения, а уже обсуждается их одежда, вкусы, походка и любимый род занятий.
Однако такой взгляд не верен. Нерешенная проблема не должна тормозить развитие науки. В математике, в компьютерных науках существует несколько недоказанных (или недоказуемых) фундаментальных утверждений-гипотез, принятие которых позволило получить большое количество важных результатов. Достаточно вспомнить тезис Тьюринга, тезис Черча
Введем еще один класс задач - NP-полные (NPС задачи (проблемы). Проблема Т называется NP-полной, если она удовлетворяет двум условиям:
1) Т NP;
2) Если R NP то R сводится к T за полиномиальное время.
NP-полные проблемы являются своего рода универсальными. Не нужно придумывать алгоритмы для других задач, достаточно свести эти задачи к какой-либо NP-полной проблеме и воспользоваться алгоритмом ее решения.
С тех пор как С. Кук доказал в 1971 г., что проблема выполнимости для пропозиционального исчисления является NP-полной, множество NPC пополнилось сотнями проблем.
NP-полные проблемы, как следует из определения, являются наиболее трудными в классе NP.
Значение класса NP-полных проблем состоит еще и в том, что ему принадлежат очень многие известные и важные в прикладном отношении задачи. Перечислим некоторые из них.
