3. Приведение дифференциальных уравнений высших порядков к нормальному виду

Пусть система n-го порядка описывается уравнением:

. (3.11)

Чтобы уравнение (3.11) имело единственное решение необходимо задание начальных условий.

x(t₀)=x₀,

, (3.12)

.

Введя новые неизвестные функции, можно привести уравнение (3.11) к системе nдифференциальных уравнений первого порядка. Такую систему называют нормальной системой дифференциальных уравнений:

Пусть

x(t)=x₁(t),

тогда

_,

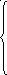
… (3.13)

_,

_.

Совокупность уравнений (3.13) можно записать следующим образом:

.(3.14)

Уравнение (3.14) в матричном виде:

. (3.15)

Решение нормальных систем дифференциальных уравнений возможно любым из изложенных выше методов.

4. Приведение матричного уравнения к новым координатам

Аналитическое решение системы нормальных дифференциальных уравнений (3.15) осложняется в случае, если матрица А недиагональная. Так как

.

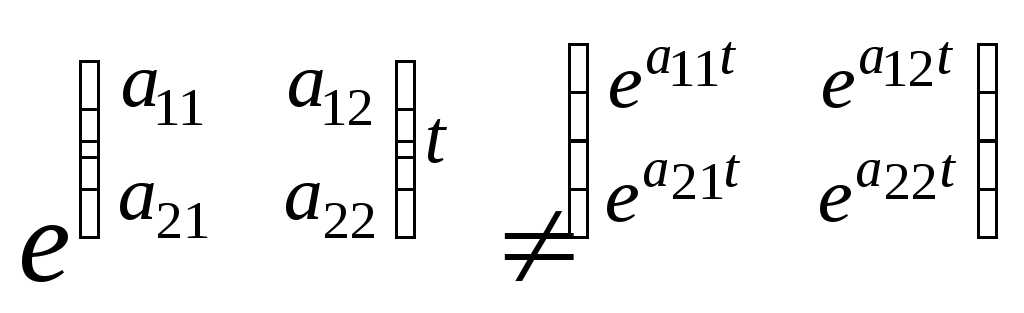Для нахождения значений можно привести уравнение (3.15) к новым координатам, в которых матрица, подобная А была бы диагональной.

Уравнение n-го порядка (3.15) в векторно-матричном виде подвергнем неособым преобразованиям,

x(t) = Тy(t),(3.16)

где Т– неособая матрица (имеет обратную матрицу) перехода к новой системе координатy. Откуда

,

подставим в исходное уравнение (3.15):

.

Последнее выражение умножим на Т^-1слева:

.

Обозначим

, (3.17)

где – диагональная матрица собственных значений матрицыA.

Окончательно приходим к уравнению:

. (3.18)

В уравнении (3.18) две неизвестные матрицы – иТ^-1. Элементы матрицы– собственные значения матрицыАможно найти двумя способами:

1. из характеристического уравнения:

, (3.19)

здесь Е– единичная диагональная матрица.

2. В MathCadдля расчета собственных значений матрицы используется функцияeigenvals(A). АргументАфункцииeigenvals– матрица. Функция возвращает собственные значения аргумента.

Для нахождения матрицы Тусловие (3.17) умножим слева наТ:

,

. (3.20)

Для того чтобы получить Ттакое, чтобы оно диагонализировало матрицуА, необходимо найти решение уравнения (3.20).

В MathCadможно воспользоваться функцией расчета нормализованной матрицы (составленной из собственных векторов матрицы-аргумента) с помощью функцииeigenvecs(A). АргументАфункцииeigenvecs– исходная матрица А. Функция возвращает системообразующую матрицу Т, преобразующую матрицу А к канонической (диагональной) форме Это возможно, если корни характеристического уравнения различные.

После определения элементов матриц – иТ. можно воспользоваться известной формулой решения систем дифференциальных уравнений в матричном виде (3.9). Для уравнения (3.15) в случае размера матриц 2 х 2 решение имеет вид:

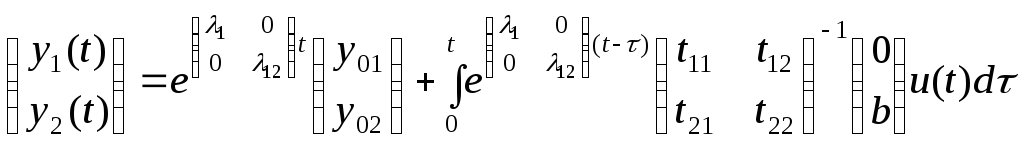, (3.22)

где

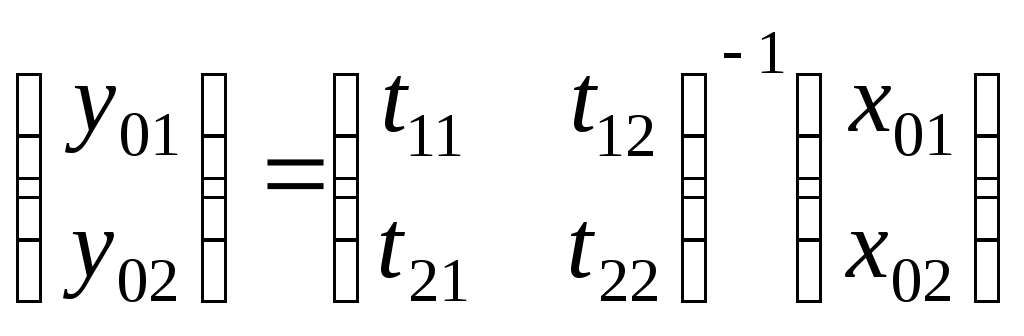. (3.22)

Искомая функция x(t):

.

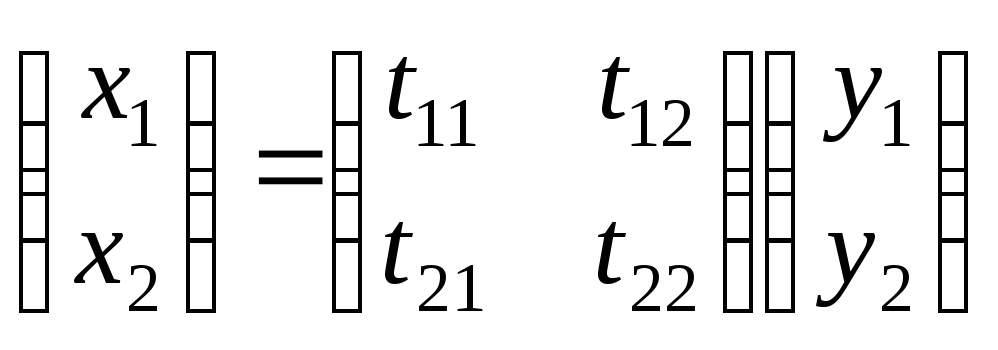5. Решение матричного уравнения с помощью теоремы Лагранжа-Сильвестра

Метод позволяет получить аналитическое решение системы нормальных дифференциальных уравнений (3.15) в случае, если матрица А недиагональная, не прибегая к линейному преобразованию координат. Матрица e^Atпредставляет собой фундаментальную матрицу системы Ф(t). Рассчитать значения элементов матрицы Ф(t) можно с помощью теоремы Лагранжа-Сильвестра.

.

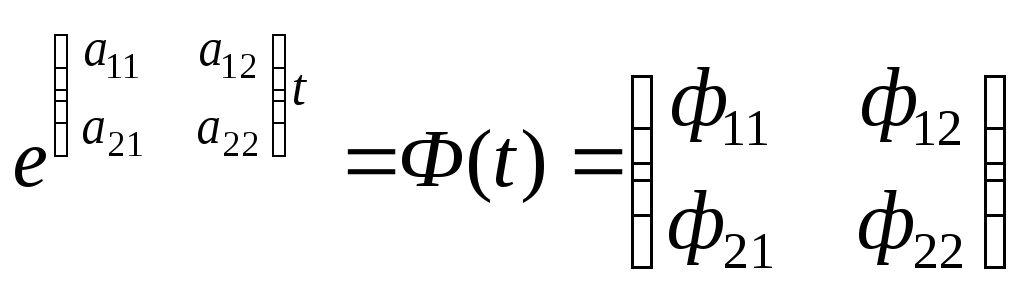Теорема утверждает, что ряд от матрицы сходится к конечной сумме, где_i– собственные значения матрицы А.

. (3.23)

Для функции f(A) = e^Atс учетом (3.23) получаем:

. (3.24)

Таким образом, для матрицы А, размером 2х2 имеем:

, (3.25)

для матрицы размером 3х3:

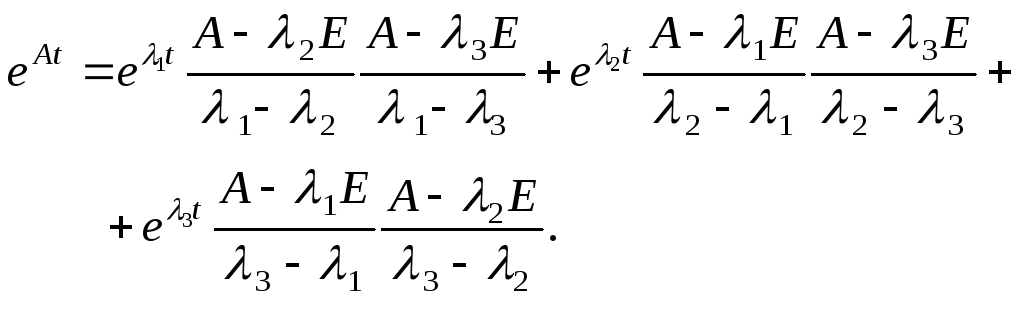. (3.26)