Информатика / лекции

program ddd; var x,y,z:real; begin

writeLn('табуляция функции cos(y*sin(x*x*x)):'); y:=-2;

while y<=1 do begin

x:=13;

while x<=15 do begin

z:=cos(y*sin(x*x*x)); if z<0.6 then

writeLn('z(',x:6:3,', ',y:6:3,') =',z:6:2); x:=x+0.8;

end;

y:=y+1;

end;

end.

В результате на консоли появится сообщение:

табуляция функции cos(y*sin(x*x*x)): z(13.000, -2.000) = -0.14

z(13.800, -2.000) = -0.40 z(14.600, -2.000) = -0.28 z(13.800, -1.000) = 0.55 z(13.800, 1.000) = 0.55

Рассмотрим еще одну интересную задачу.

ПРИМЕР

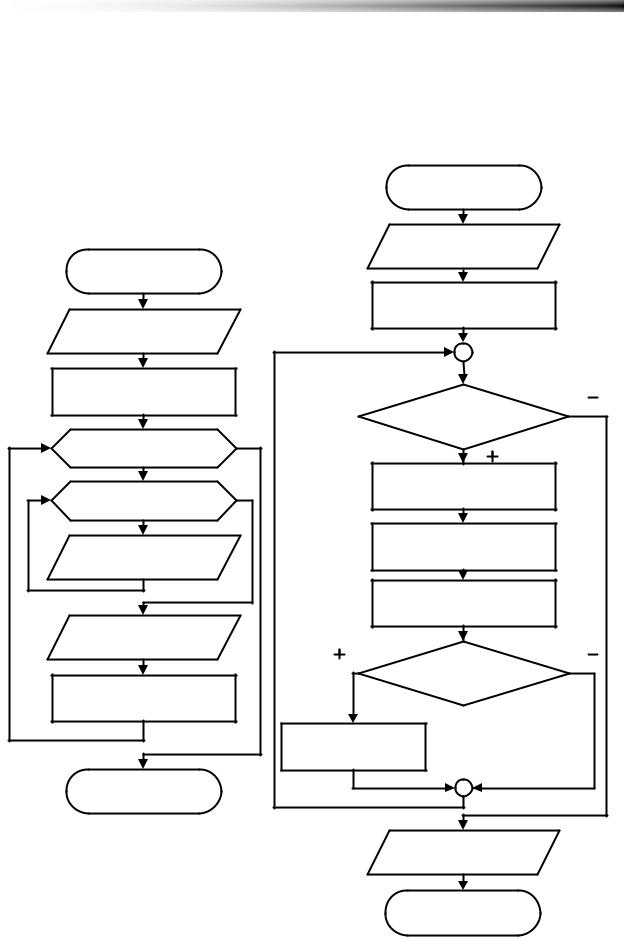
Для функции y =ex / x2 где x изменяется от точки x =1 с шагом x = 0,5 в положительном направлении, определить на каком шаге будет выполнено условие y >104 .

Решение задачи достаточно простое и представлено на блок-схеме

(Рисунок 4.10).

Программная реализация: program ddd;

var x,y:real; k:integer;

begin

x:=1; k:=0; repeat

y:=exp(x)/sqr(x);

inc(k);

x:=x+0.5; until y>1e4;

writeLn('условие достигается в точке ', x:8:1); writeLn('на ',k,'-м шаге' );

end.

82 4.2 Задачи на использование циклов

Стоит отметить, что даже поиск максимума, по своей сути рекуррентен, поскольку каждое последующее его значение основано на предыдущем (хотя и не так явно, как в операциях присваивания).

Практически всегда, когда производят расчет суммы, за начальное значение принимают ноль. Рассмотрим, например, такую задачу:

ПРИМЕР

6

Найти значение суммы S = ∑k 2 . Расписывается эта сумма достаточно

k =1

просто S =12 + 22 +32 + 42 +52 +62 . В результате будем иметь 91. Блок схема изображена на (Рисунок 4.11 а)).

Рисунок 4.11 Задачи на поиск суммы (а)) и произведения (б))

program SumS; var s:real;

k,N:integer; begin

s:=0;

for k:=1 to 6 do s:=s+sqr(k);

writeLn('сумма равна ', s:8:2); end.

При решении задач на произведения в качестве начального значения принимают 1.

ПРИМЕР

Найти значение выражения P = 2N не используя операцию возведения в

N

степень. Эта задача эквивалентна расчету такой формулы: ∏2 = 2 2 2 ... 2

k =1

(всего N двоек). Решение показано на (Рисунок 4.11 б)). program PrP;

var k,N:integer; P:longInt;

begin

writeLn('введите N'); readLn(N);

p:=1;

readLn(N); S_ext:=0;

for k:=1 to N do begin

S_int:=0;

for j:=k to 2*k do S_int:=S_int+cos(j);

S_ext:=S_ext+k*S_int; end;

writeLn('сумма равна ', S_ext:8:2); end.

Иногда, несмотря на кажущуюся сложность, задача решается несколько проще, чем полагалось изначально.

ПРИМЕР

Найти значение суммы S = ∑N k 2 .

k =1 k!

Здесь для подсчета внешней суммы потребуется на каждой новой итерации вычислять факториал для текущего значения k . На первый взгляд, без вложенного цикла на произведение не обойтись. Однако, если посмотреть внимательно на формулу и вспомнить замечательное свойство факториала заключающееся в том, что для вычисления последующего значения достаточно знать предыдущее, то алгоритм запишется намного короче (Рисунок 4.13 а)). И, что самое главное, без вложенных циклов.

На комбинацию program ddd; var s:real;

f,k,N:integer; begin

cls; writeLn('введите N'); readLn(N);

s:=0;

f:=1;

for k:=1 to N do begin

f:=f*k;

s:=s+sqr(k)/f;

end;

writeLn('сумма равна ', s:8:2); end.

ПРИМЕР

Найти значение выражения x + x + x +... (всего 20 корней).

Для вычисления этого выражения необходимо самостоятельно придумать рекуррентную формулу. Это уже будет и не сумма и не произведение, а нечто более сложное. Чтобы понять, какая формула здесь

S := S + k2/f

Вывод S

Вывод S

Конец

Рисунок 4.13 Сложная сумма - а) и нестандартная рекуррентная формула - б)

применяется, можно последовательно начать расписывать вычисляемое значение на каждом шаге. Итак,

начальное значение, достаточно просто составить алгоритм для вычисления

S (Рисунок 4.13 б)).

Программа представлена ниже: program sqrtS;

var k:integer; x,s:real;

begin cls;

writeLn('введите x'); readLn(x);

s:=0;

for k:=1 to 20 do s:=sqrt(x+s);

writeLn('s равно ', s); end.

При x=30 сумма получается равной 6, а, например, при x=7, она становится такой: 3.19258240356725.

Весьма интересными являются задачи на перекрестные рекуррентные зависимости. Перекрестными рекуррентными зависимостями называют такие, у которых каждое последующее значение вычисляется на основе нескольких предыдущих значений. Самый простой пример – это авторегрессионные последовательности. Наиболее известная последовательность задаваемая рекуррентно на основе двух предыдущих значений является последовательность Фибоначчи. Последовательность задается таким образом: a1 =1 , a2 =1, a3 = a1 + a2 , a4 = a3 + a2 , ak = ak −2 + ak −1 .

ПРИМЕР

Вывести 10 первых членов последовательности Фибоначчи.

Решается задача в один цикл. Решение представлено на (Рисунок 4.14

а)).

Ниже идет программа: program ddd;

var ak_3,ak_2,ak_1,ak:real; k:integer;

begin ak_2:=1; ak_1:=1; k:=2;

writeln(1:5,' z=',ak_1); writeln(2:5,' z=',ak_2); repeat

ak:=ak_1+ak_2; ak_2:=ak_1; ak_1:=ak; inc(k);

writeln(k:5,' z=',ak); until k=10;

end.

8z=21

9z=34

10z=55

Можно несколько модифицировать предыдущую последовательность и сделать так, чтобы в авторегрессионной формуле участвовало три предыдущих члена.

ПРИМЕР

Вывести N ( N ≤3 ) первых членов последовательности заданной рекуррентно ak = ak −1 + ak −2 + ak −3 , a1 =1 , a2 = 2 , a3 =3.

При решении этой задачи важно понять суть перехода от пары переменных к трем. В алгоритме на каждой итерации применяется так называемый циклический сдвиг переменных. Т.е. переменные принимают значения тех, которые им предшествуют. Ну а самая последняя, т.е. текущая переменная принимает свое значение согласно заданной рекуррентной формуле (Рисунок 4.14 б)). Имена переменным даны согласно порядку их расположения в последовательности, т.е. ak = ak , ak −1 = ak _1, ak −2 = ak _ 2 ,

ak −3 = ak _ 3 . Программа такова:

program ddd;

var ak_3,ak_2,ak_1,ak:real; k,N:integer;

begin

writeLn('введите N'); readLn(N);

while N<=3 do begin

writeLn('введите N'); readLn(N);

end; ak_3:=1; ak_2:=2; ak_1:=3; k:=3;

writeln(1:5,' z=',ak_3); writeln(2:5,' z=',ak_2); writeln(3:5,' z=',ak_1); repeat

ak:=ak_1+ak_3+ak_2; ak_3:=ak_2; ak_2:=ak_1; ak_1:=ak;

inc(k);

writeln(k:5,' z=',ak); until k=N;

end.