Калинин / Приборостроителям / Математика 1 (6)

8

Даны вершины треугольника. Найти:

1. длину стороны ВС;

2. уравнение высоты ВС;

3. уравнение высоты, проведённой из вершины А;

4. длину высоты, проведённой из вершины А;

5. угол В.

Сделать чертёж.

Дано: А(-8;3), В(4;-2), С(7;2).

РЕШЕНИЕ

1. Длину стороны ВС находим по формуле 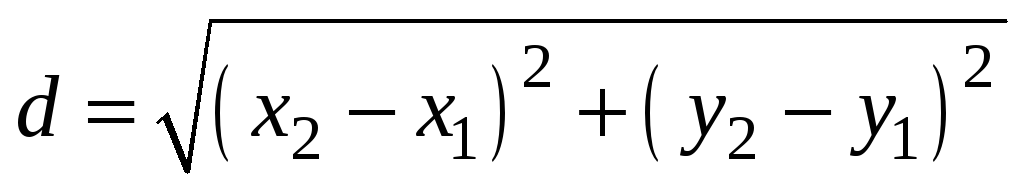. По условию имеем В(4;-2), С(7;2).

2. Найдём уравнение стороны ВС. Найдём уравнение прямой, на которой лежит сторона ВС. Используем уравнение прямой, проходящей через две точки 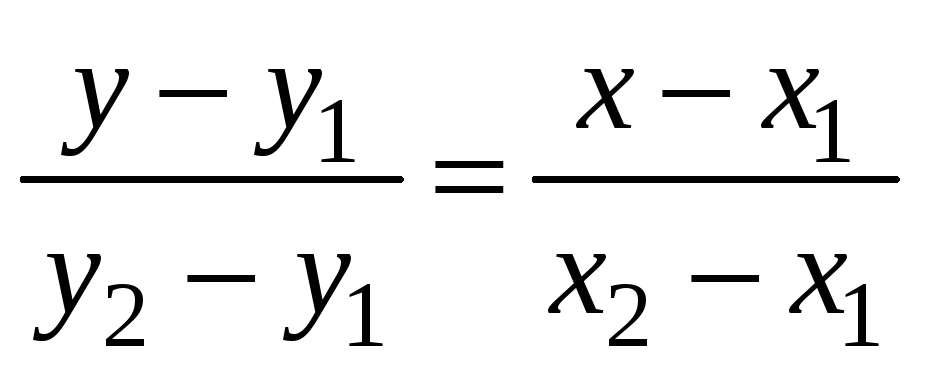, полагая

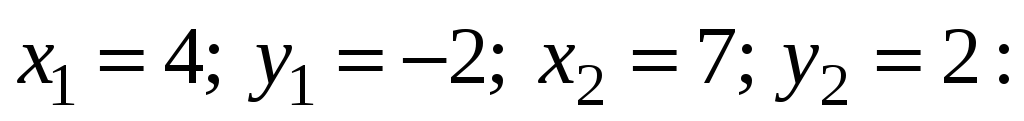
3. Найдём уравнение высоты, проведённой из вершины А. При составлении уравнения прямой, на которой лежит высота треугольника, воспользуемся формулой 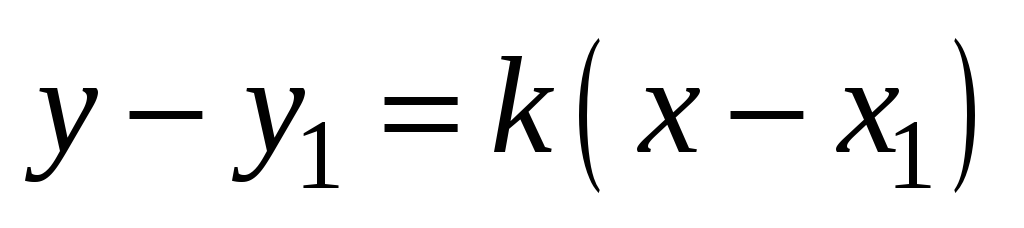и условием перпендикулярности двух прямых :

Определим угловой коэффициент прямой ВС. Для этого разрешим уравнение стороны ВС относительно у:

Следовательно, высота, проведённая из точки А, имеет угловой коэффициент

Тогда, уравнение высоты, опущенной из вершины А(-8;3) на сторону ВС:

4. Найдём длину высоты, проведённой из вершины А. Она равна расстоянию от точки А(-8;3) до прямой ВС заданной уравнением . По формуле 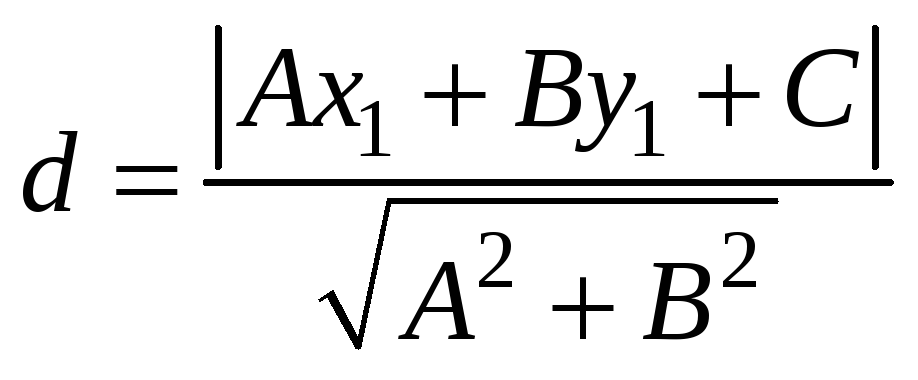вычисляем расстояние от точки А до прямой ВС, полагая

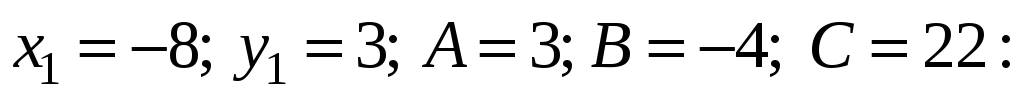
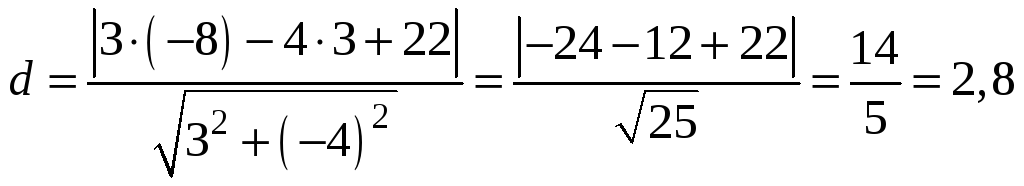
5. Найдём угол В. Угол В равен углу между прямыми ВС и АВ и может быть найден с помощью формулы 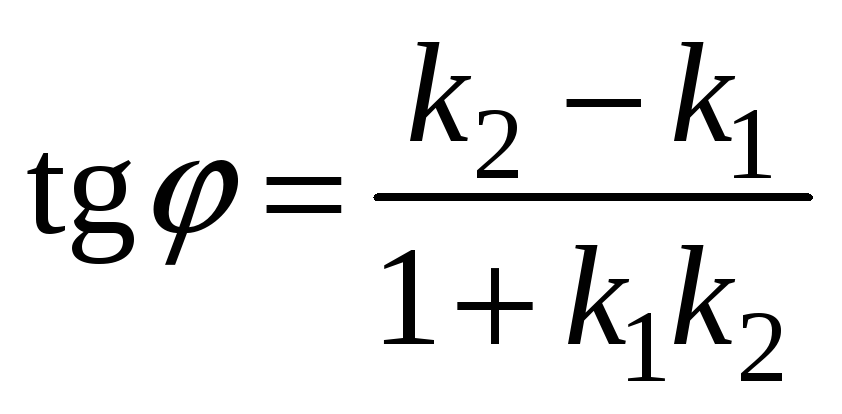. Угловой коэффициент прямо ВС известен и равен 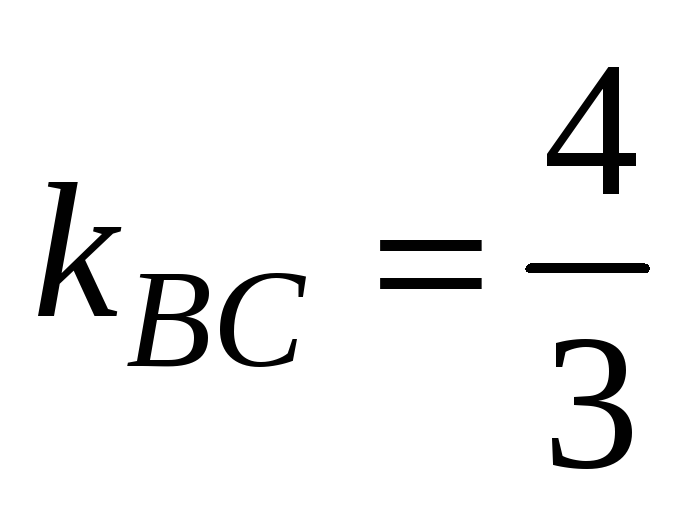. Найдём угловой коэффициент прямой АВ по формуле:

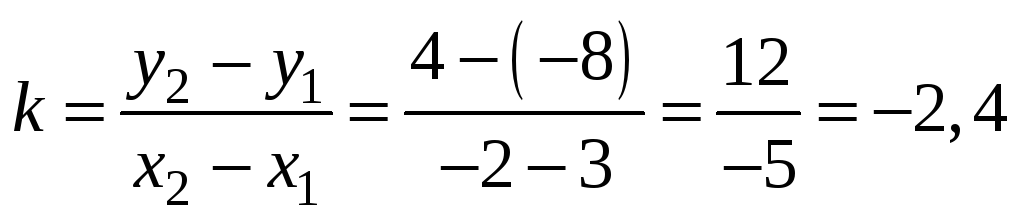
Тогда получаем,

И угол равен

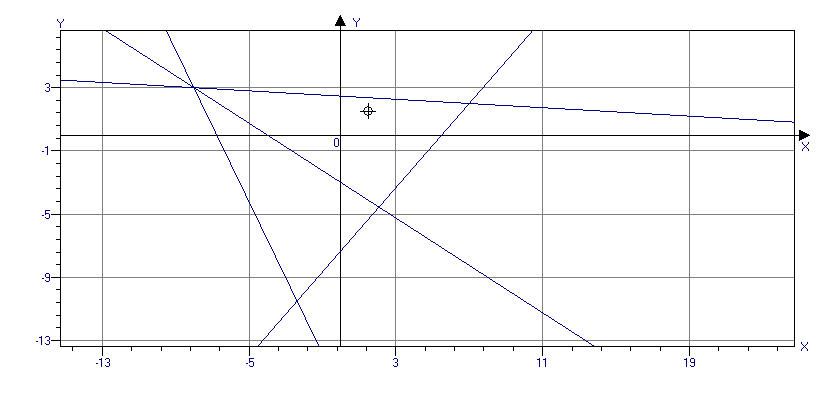
Выполним чертёж. В прямоугольной декартовой системе координат хОу строим исходные точки и получаем треугольник АВС. Затем из вершины А опустим перпендикуляр на сторону ВС, получим АК.

18

Даны координаты вершин пирамиды А₁А₂А₃А₄. Найти:

1. координаты вектора и длину ребра ;

2. угол между рёбрами 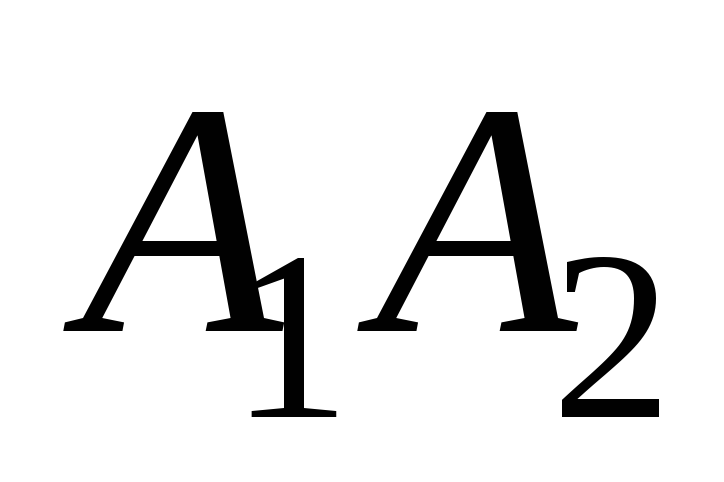и ;

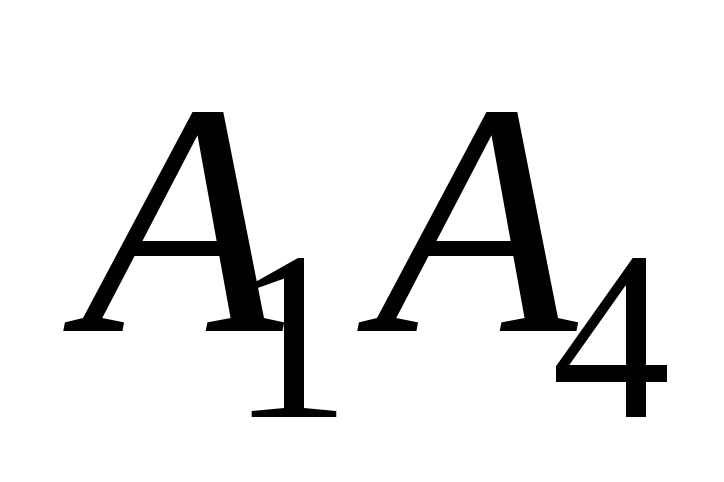3. площадь грани ;

4. объём пирамиды;

5. уравнение плоскости ;

6. уравнение прямой ;

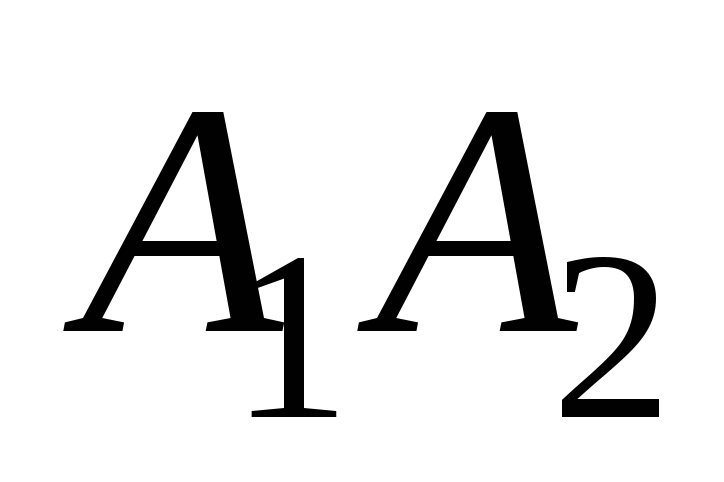7. угол между ребром 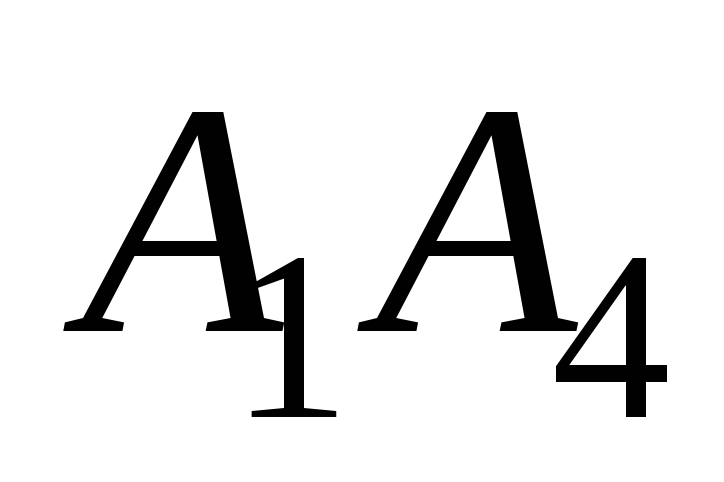и гранью ;

8. уравнение высоты, опущенной из вершины на грань ;

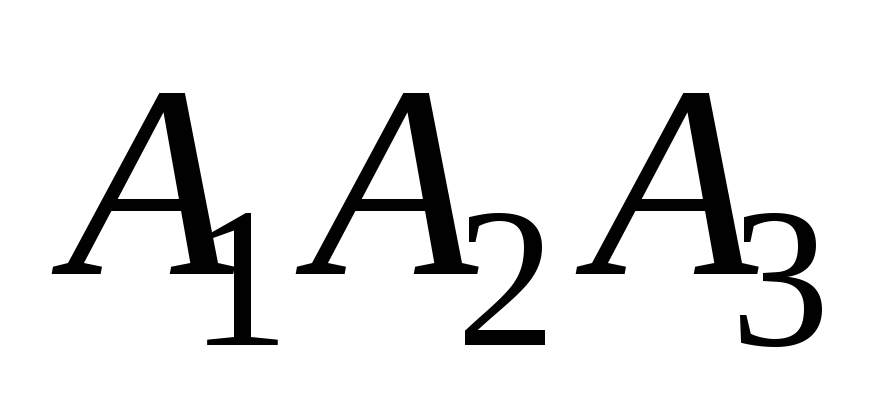Сделать чертёж.

Дано: А₁(7;2;2), А₂(5;7;7), А₃(5;3;1), А₄(2;3;7).

РЕШЕНИЕ

1. Вектор 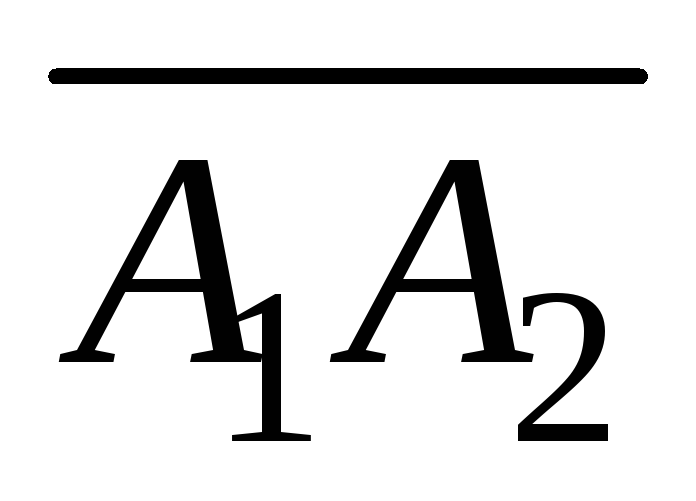равен

Длину ребра можно найти как расстояние между двумя точками и , оно равно

Получаем

2. Угол между рёбрам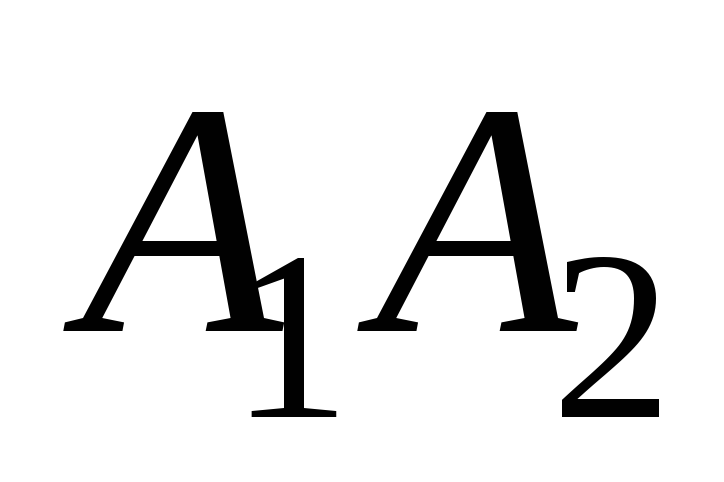и и 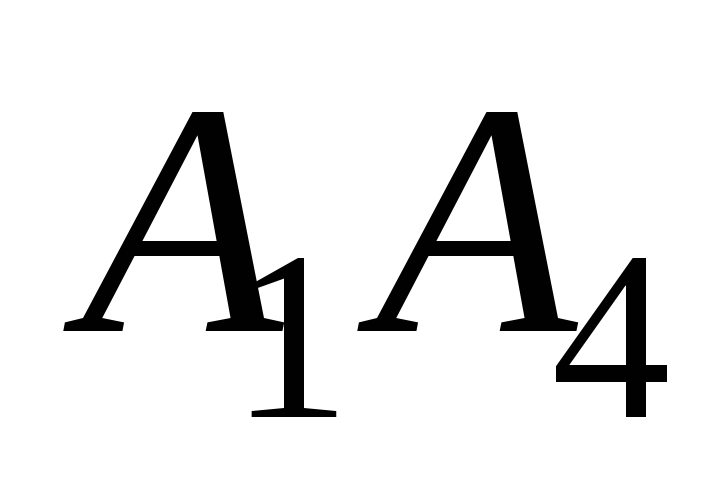найдём как угол между векторам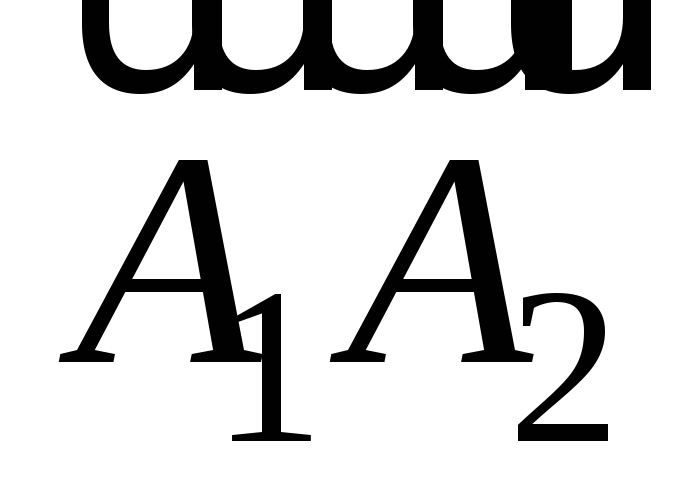и и .

Вектор

Таким образом, имеем два вектора и , угол между ними найдём по формуле:

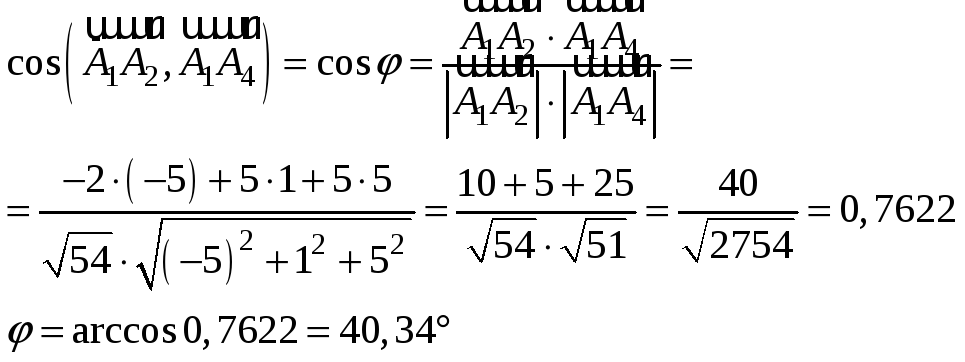
Скалярное произведение двух векторов в числителе дроби находили как сумму произведений одноимённых координат (проекций).

3. Площадь грани равна половине площади параллелограмма, построенного на векторах, как на сторонах. И площадь треугольника 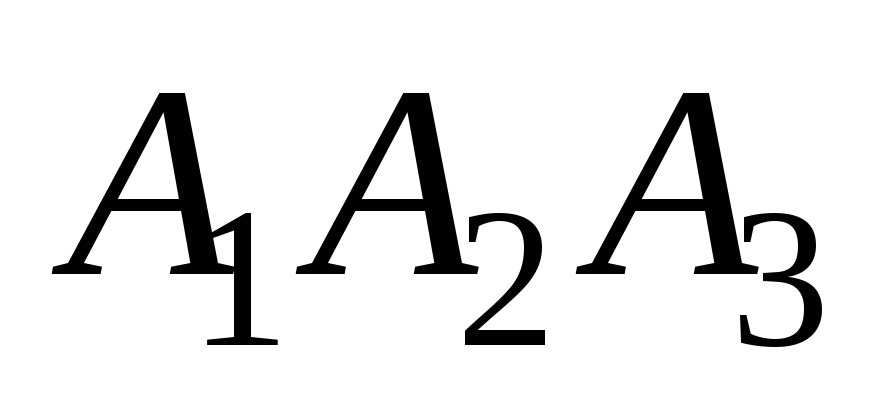можно вычислить через векторное произведение

Координаты вектора или

Векторное произведение вычислим через определитель 3-го порядка, разложив его по элементам первой строки:

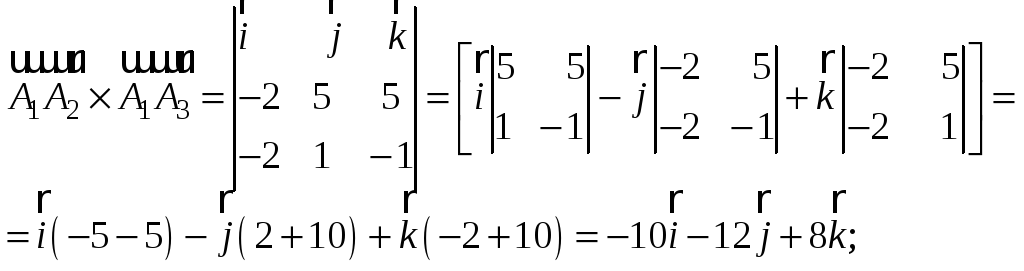
Модуль векторного произведения

4. Объём треугольной пирамиды А₁А₂А₃А₄ можно рассматривать как одну шестую часть объёма параллелепипеда, построенного на векторах , и как на рёбрах:

Смешанное произведение трёх векторов равно

5. Уравнение плоскости имеет вид

или для нашей задачи

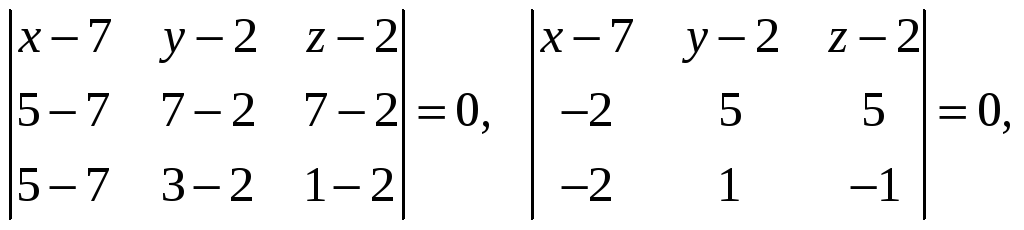
Разложим определитель по элементам первой строки:

6. Уравнения прямой найдём в канонической форме, для этого воспользуемся уравнением прямой, проходящей через две заданные точки и :

,

7. Углом ψ между ребром и гранью 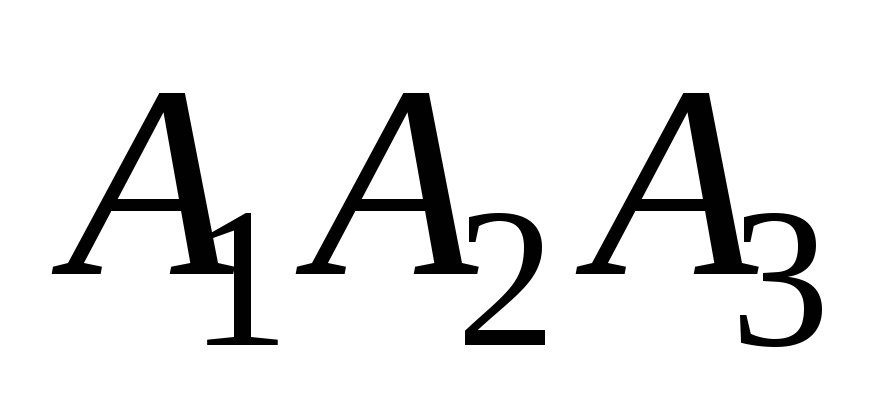будет острый угол между прямой и её проекцией на плоскость 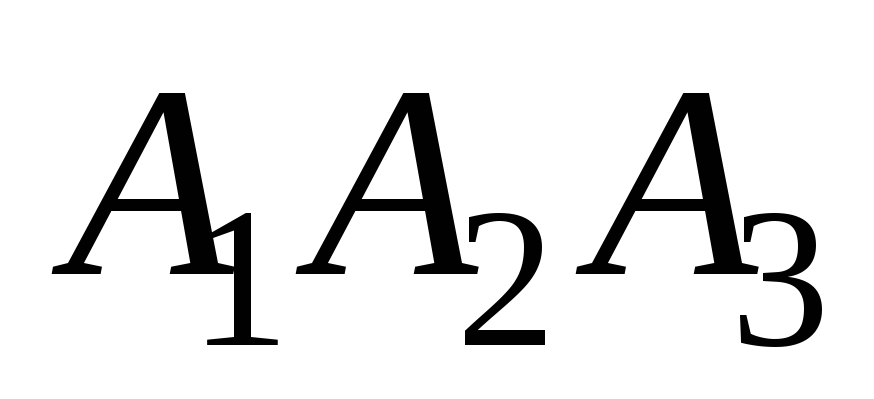. Для нахождения угла ψ воспользуемся формулой

Канонические уравнения прямой получим как:

Отсюда l=5; m=1; n=-5, где l, m, n – координаты направляющего вектора прямой :

;

Уравнение плоскости было получено в пункте 5:

Отсюда А=5; В=7; С=-4, где А, В, С – координаты нормального вектора плоскости :

Тогда получаем

8. Уравнения высоты, опущенной из вершины на грань .

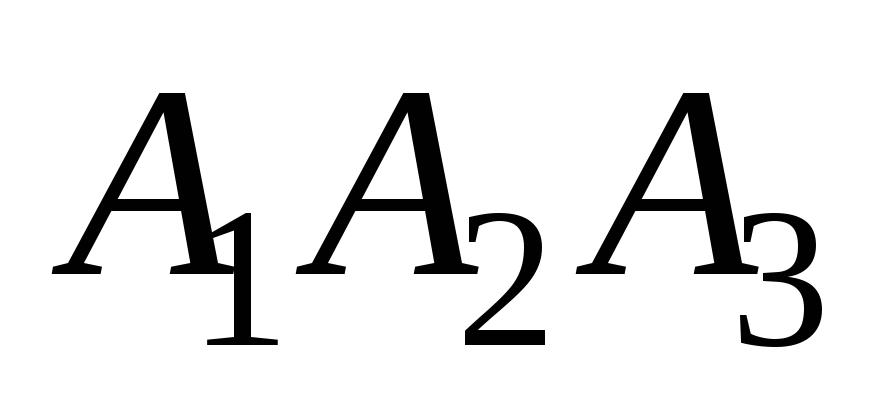Канонические уравнения прямой, проходящей через точку , имеют вид , где l, m, n – координаты направляющего вектора прямой.

Так как высота перпендикулярна плоскости , то из условия перпендикулярности прямой и плоскости координаты направляющего вектора прямой, перпендикулярной плоскости можно заменить координатами нормального вектора плоскости l=A=5; m=B=7; n=C=-4.

Окончательно получим

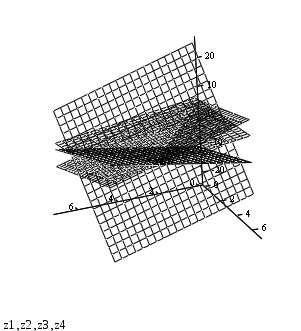
Выполним чертёж пирамиды как пересечения плоскостей её граней:

Грань А₁А₂А₄:

Грань А₁А₂А₃:

Грань А₁А₃А₄:

Грань А₂А₃А₄:

28

Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности

РЕШЕНИЕ

В системе координат хОу строим ось ординат х=0 и окружность

Пусть точка М(х; у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляры на ось ординат и на окружность.

Тогда расстояние от произвольной точки М(х; у) до оси ординат – абсцисса точки М(х; у), а расстояние от точки М(х; у) до окружности . Приравнивая эти расстояния и снимая знак модуля, получаем

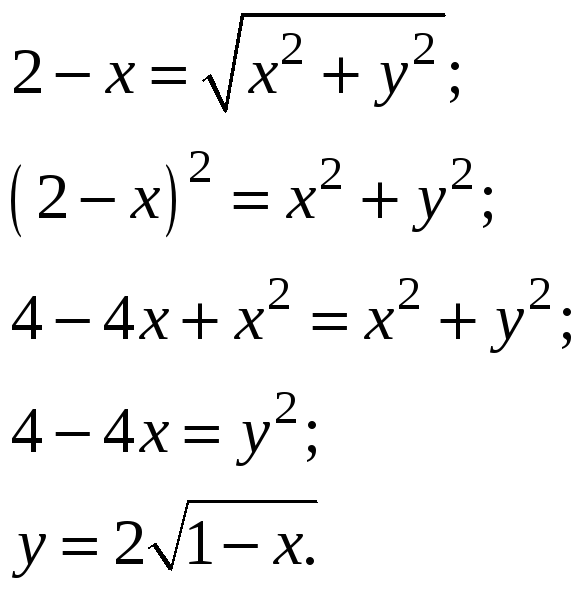
Получили уравнение параболы, строим верхнюю часть окружности и параболы, так как чертёж симметричный: