Задание к-7. Определение абсолютной скорости и абсолютного ускорения точки при сложном движении

Прямоугольник ABCDвращается вокруг оси, проходящей через вершинуА, по закону. Ось вращения перпендикулярна плоскости прямоугольника (рис. 5). По круговому каналу радиусаR=10cм с центром в точке С, расположенному на прямоугольнике, движется точка М. Дуговая координата точки меняется по законусм. Дано:АВ=12см,ВС=15 см.Найти абсолютную скорость и абсолютное ускорение точки при.

Движение точки М представим в виде относительного движения по круговому каналу и переносного движения вместе с вращающимся прямоугольником.

Рис.5

1. Вычисляем значение дуговой координаты прии определяем положение точки в подвижной системе координат. За времяточка проходит по дуге окружности путьсм. Центральный угол, соответствующий этой дуге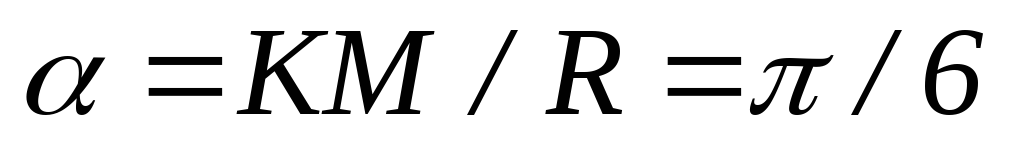. Изображаем точку в этом положении (рис.6).

2. Дифференцируя по времени, получаем выражение относительной скорости точки, а подставив, определим ее значение в заданный момент времени

Вектор направлен по касательной к траектории относительного движения точки.

3. Вычисляем радиус траектории переносного движения точки

4. Находим переносную скорость точки. Переносной скоростью точки является скорость той точки прямоугольной пластинки, с которой в данный момент времени совпадает движущаяся точка М. Переносная угловая скорость равна

.

Отсюда .

Рис.6

5. Определяем модуль абсолютной скорости точки. Для этого проецируем векторное равенство на подвижные оси координатxиy, жестко связанные с движущейся пластинкой.

Тригонометрические функции угла рассчитываем по формулам

Модуль абсолютной скорости точки

6. Вычисляем относительное ускорение. Ускорение точки, движущейся относительно пластинки по дуге окружности, имеет нормальную и тангенциальную составляющие

Модуль относительного ускорения

Вектор относительного нормального ускорения точки направлен по радиусу окружности к точкеС, вектор относительного касательного ускорениянаправлен по касательной к траектории относительного движения точки в сторону увеличения дуговой координатыКМ, так как(Рис. 7).

Рис.7

7. Вычисляем переносное ускорение точки . Траектория переносного движения точки – окружность радиусас центром в точкеА. Прямоугольник вращается с угловой скоростьюи угловым ускорением

Отсюда получаем

Модуль переносного ускорения точки

Вектор переносного центростремительного ускорения направлен по радиусу кривизны к центру кривизны траектории переносного движения, т.е. к точкеА. Вектор переносного вращательного ускорениянаправлен также как и переносная скорость точки, так как знаки переносной угловой скоростии переносного углового ускоренияодинаковы.

Рис.8

8. Находим ускорение Кориолиса. Модуль вектора ускорения определяем по формуле, где- угол между векторами переносной угловой скоростии относительной линейной скорости. Векторперпендикулярен плоскости чертежа, т.е.. Имеем

Направление вектора ускорения Кориолиса получаем по правилу Жуковского – поворотом на вектора относительной скорости точки по направлению переносного вращения, т.е. против часовой стрелки (рис. 8).

9. Находим абсолютное ускорение точки по векторному выражению

,

проецируя его на оси координат. Так как все составляющие вектора абсолютного ускорения точки лежат в плоскости чертежа, то достаточно спроецировать их на две оси и(см. рис. 7).

Находим модуль ускорения

.

Ответы заносим в таблицу. Радиус траектории переносного движения – в , скорость – в, ускорение – в.

Таблица 5

9,44	15,71	28,33	14,21	39,75	87,07	94,25	50,97