2.2.2. Определение скорости точки при задании её движения координатным способом

Учитывая известную из математики теорему о том, что проекция производной от вектора на какую-либо неподвижную ось равна производной от проекции вектора на ту же ось, а также выражение для вектора скорости через его проекции на оси координат

, (11)

и уравнения(3), (6) и (10) получим выражения для определения проекций скорости на оси координат

; ; (12)

Проекции скорости точки на неподвижные оси координат равны первым производным от соответствующих координат точки по времени.

Сокращённо можно получить:

, ,.(13)

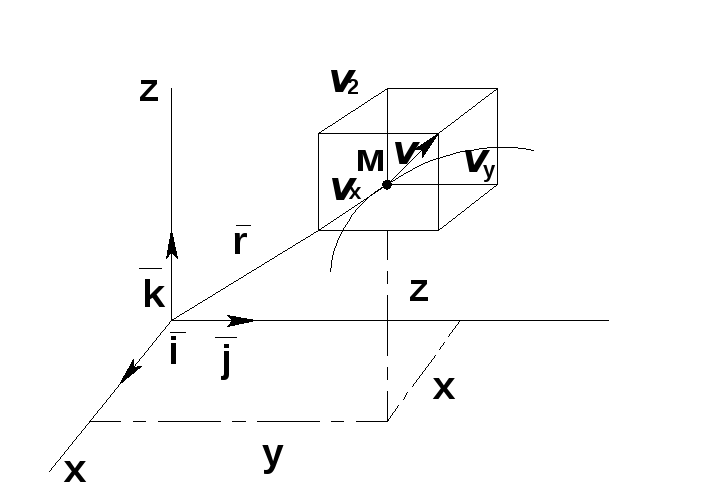
Построив прямоугольный параллелепипед, рёбра которого параллельны осям координат, а диагональ совпадает со скоростью , получим проекции скорости на соответствующие оси координатv_X, v_Y, v_Z.

Тогда модуль скорости точки:

. (14)

Направление вектора можно вычислить по соответствующим формулам:

(15)

2.2.3. Определение скорости точки при задании её движения естественным способом

Для определения скорости точки в случае, когда движение задано естественным способом, необходимо чтобы было известно: траектория движения АВ, начало и направление отсчёта дуговой координаты, и уравнение движения точки (см. рис. 6).

П

Рис. 6

усть в момент времениt точка

занимает положение М, в момент времени t₁ = t + ∆t – положение М₁. Соответственно дуговые координаты этих положений точки имеют значения:

S = OM; S₁ = OM₁ = OM + MM₁ = S + S,

где S – приращение дуговой координаты

S =ММ₁.

Проведя из центра С в точку М радиус-вектор , определим скорость точки в момент времениt

. (16)

Так как радиус-вектор зависит от дуговой координатыS, т.е. , то:

, (17)

где .

По направлению вектор совпадает с вектором, но, т.е. векторимеет модуль, равный единице и направлен по касательной к кривойАВ в сторону увеличения дуговой координаты. Кроме того, вектор является ортом этого направления. Обозначим этот орт(см. рис. 6). Используя формулу(17) можно показать, что

, (18)

где производная представляет собой проекцию вектора скоростина касательную:

. (19)

Тогда модуль вектора скорости равен абсолютному значению производной от дуговой координаты точки по времени:

(20)

2.3. Определение ускорения точки

2.3.1. Определение ускорения точки при векторном способе задания ее движения

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления вектора скорости точки.

П

Рис. 7

усть в некоторый момент времениt движущаяся точка находится в положении М и имеет скорость _, а в момент времени t₁ приходит в положение М₁ и имеет скорость , тогда за промежуток времени Δt = t₁-t скорость точки получает приращение . Векторвсегда направлен в сторону вогнутости траектории точки.

Отношение приращения вектора скорости к соответствующему промежутку времениΔt определяет вектор среднего ускорения точки за этот промежуток времени:

(21)

Вектор среднего ускорения имеет, очевидно, то же направление, что и вектор, то есть направлен в сторону вогнутости траектории точки.

Ускорением точки в данный момент времени t называется векторная величина, к которой стремится среднее ускорение при стремлении промежутка времениΔt к нулю.

(22)

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Найдем как располагается вектор по отношению к траектории точки. При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения , также как и вектор лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то векторбудет направлен в сторону вогнутости траектории и будет лежать в плоскости, проходящей через касательную к траектории в точкеМ и прямую, параллельную касательной в соседней точке М₁. В пределе, когда точка М₁ стремится к М эта плоскость занимает положение так называемой соприкасающейся плоскости. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.