Bilety / 37

37. Дифференцируемость и полный дифференциал ФНП. Необходимые признаки дифференцируемости (непрерывность и частные производные). Примеры.

Полное приращение и полный дифференциал ФНП

Полным приращением функции двух переменных z = f (x, y) в точке (x, y), вызванным приращениями аргументов  и , называется выражение .

Функция z = f (x, y) называется непрерывной в точке (x, y), если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции.

Если обозначить  – расстояние между близкими точками  и (х, у), то  – это определение непрерывности ФНП на языке приращений.

Если функция z = f (x, y) непрерывна в любой точке (х, у)ÎD, то она называется непрерывной ФНП в области D.

 Функция z = f (x, y), полное приращение Dz которой в данной точке (x, y) может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно и , и величины, бесконечно малой более высокого порядка малости относительно , называется дифференцируемой ФНП в данной точке, а линейная часть ее полного приращения называется полным дифференциалом ФНП.

Если , где  –бесконечно малые при , то полный дифференциал функции z = f (x, y) выражается формулой: 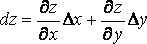, или:  (1)

(приращения независимых переменных совпадают с их дифференциалами: Dх = dx, Dy = dy).

Из определения полного дифференциала следует его связь с полным приращением: при малых  и  полное приращение функции Dz примерно равно ее полному дифференциалу:  с точностью до бесконечно малых более высокого порядка малости относительно .

Полный дифференциал функции z = f (x, y) зависит как от точки M(x0, y0), в которой он вычисляется, так и от приращений  и .

Производные ФНП высших порядков

Пусть функция z = f (x, y) имеет в точке (x, y) и её окрестности непрерывные частные производные первого порядка  и . Так как  и  являются функциями тех же аргументов x и y, то их можно дифференцировать по x и по y. При этом возможны следующие 4 варианта:

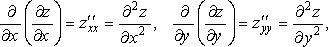
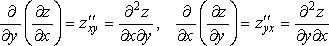
– эти частные производные называются частными производными второго порядка от функции z (x, y).

Частные производные  и  называются смешанными частными производными второго порядка.

Пример. Дана ФНП . Вычислим все её частные производные второго порядка.

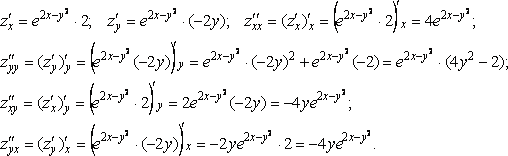
Основное свойство смешанных частных производных: если функция z = f (x, y) и её частные производные , ,  и  определены и непрерывны в точке (x, y) и некоторой её окрестности, то в этой точке =, то есть смешанные частные производные при условии их непрерывности не зависят от порядка, в котором производится дифференцирование.

 

Задача 2. Вычислить пределы числовых последовательностей.

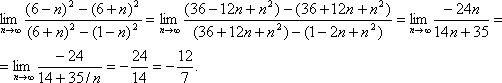
Задача 3. Вычислить пределы числовых последовательностей.

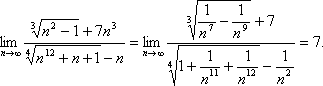
Задача 4. Вычислить пределы числовых последовательностей.

……u=А₁x₁+…+А_nx_n+_x₁+…+_nx_n (2), где A₁,...,A_n=const, _i=_i(x₁,...,x_n) – бесконечно малая при (x₁,…,x_n)->0, т.е. i : lim(_i(x₁,..,x_n))=0 при (x₁,…,x_n)->0. Причем при (x₁,…,x_n)=0 будем полагать (₁,...,_n)=0.

Другие формы условия дифференцируемости (2): Пусть =(x+x, x) – расстоянию между х и х+х. Т.е. =(x₁² +…+ x_n²)^1/2. Очевидно, что lim=0 при (x₁,…,x_n)->0. |_x₁+…+_nx_n| = |_x₁/+…+_nx_n/|  (|₁|*|x₁|/+…+|_n|*|x_n|/)  (|₁|+…+|_n|)=o() при ->. Таким образом, условие дифференцируемости может быть записано следующим образом: u=А₁x₁+…+А_nx_n + o() (3), где -> при х->. и при этом условии считать, что

o()=0 при =0. Условия (2) и (3) эквивалентны