Bilety / 34

34. Вычисление объемов тел по их поперечным сечениям при помощи определенного интеграла. Вычисление объемов тел вращения. Теоремы Гульдина. Объемы трехосного эллипсоида, эллипсоида вращения и тора.

Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [x_i-1, x_i] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M_i и m_i.

  Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_ix_i и m_ix_i здесь x_i = x_i - x_i-1.

  Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно  и .

  При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

  Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.

  Пример: Найти объем шара радиуса R.

В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле .

Тогда функция площадей сечений имеет вид: Q(x) = .

Получаем объем шара:

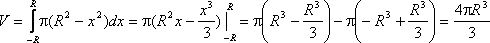
Вычисление объема тела вращения

Рассмотрим криволинейную трапецию, т.е. фигуру, образованную прямыми , , осью и функцией .

Требуется найти объем тела вращения, образованного вращением криволинейной трапеции вокруг оси .

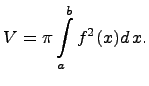
Объем данного тела вычисляется по формуле, содержащей определенный интеграл:

Если криволинейная трапеция прилежит к оси (прямые , , ось и функция ), тогда объем тела также определяется по формуле, содержащей интеграл:

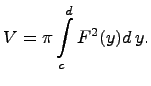
Теоремы Гульдина–Паппа

Выведем теоремы, связывающие площадь поверхности (соответственно, объем тела) вращения с центром тяжести вращающейся дуги (соответственно, криволинейной трапеции).

Пусть поверхность образована вращением дуги , имеющей длину . Мы знаем, что ордината центра тяжести этой дуги выражается формулой

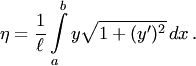
Так как площадь поверхности вращения выражается интегралом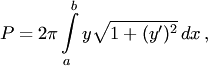

то из этого равенства следует, что .

Мы доказали следующее утверждение, называемое первой теоремой Гульдина–Паппа.

Площадь поверхности, полученной от вращения кривой вокруг непересекающей ее оси, равна произведению длины дуги этой кривой на длину окружности, описанной центром тяжести этой кривой.

Аналогично, из формулы, выражающей ординату центра тяжести криволинейной трапеции

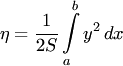и формулы объема тела вращения

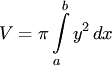
получаем , т. е. следующее утверждение, называемое второй теоремой Гульдина–Паппа:

Объем тела, полученного от вращения плоской фигуры вокруг непересекающей ее оси, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести этой фигуры.

Пользуясь этими двумя теоремами, можно в ряде случаев упростить процесс вычисления поверхности или объема тела вращения

ЭЛЛИПСОИД

Пример: найти объём эллипсоида, получающегося при вращении эллипса вокруг оси Ox. Решение: эту задачу проще решить, если применить параметрические уравнения эллипса: . Верхняя дуга эллипса получается при изменении t от 0 до , при этом точке крайней левой точке эллипса соответствует значение параметра t₀ , равное , крайней правой точке соответствует значение t_k = 0. Формула 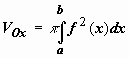для кривой, заданной параметрически,примет вид 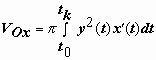, поэтому 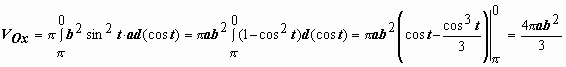. Если требуется найти объём тела, которой получается при вращении плоской фигуры ABCD вокруг оси Oy, рассуждаем по другому. Разбиваем тело на полые цилиндры радиуса x, толщины , высоты f(x). Объём этого цилиндра равен произведению длины окружности на толщину и высоты f(x); суммируя эти объёмы и переходя к пределу при , получим

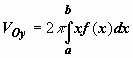
Объём тела вращения

Пусть функция f(x) непрерывна и неотрицательна на отрезке [a, b]. Тогда тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y = f(x), имеет объём

                   (52)

Пример 20. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).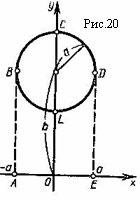

Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD  

Используя формулу (52), получаем для объёма тора v выражение