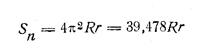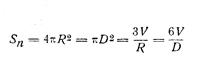Bilety / 35

35. Вычисление площадей поверхности вращения. Теоремы Гульдина. Поверхности тора и сферы.

Первая теорема Гульдина:

Величина поверхности, полученной от вращения кривой около некоторой не пересекающей ее оси, равна длине дуги этой кривой, умноженной на длину окружности, описанной центром тяжести С кривой (рис. 1)

Р = S·2πη

Эта теорема позволяет установить координату η центра тяжести кривой, если известны ее длина S и площадь Р описанной ею поверхности вращения.

Рассмотрим следующие примеры:

). Найти статический момент обвода эллипса x2/a2 + у2/b2 = 1 относительно оси x (предполагая а > b).

Для верхнего (или нижнего) полуэллипса этот момент только отсутствием множителя 2π отличается от величины соответствующей поверхности вращения. Поэтому

статический центр тяжесть гульдин

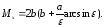
). Если рассматриваемая дуга симметрична относительно некоторой прямой, то центр тяжести дуги необходимо лежит на этой прямой.

Для доказательства примем ось симметрии за ось у, а точку ее пересечения с кривой - за начальную точку для отсчета дуг. Тогда функция х = Ф(s) окажется нечетной функцией от s и, если на этот раз длину всей кривой обозначить через 2S, будем иметь

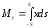=0,

откуда и ξ = 0.

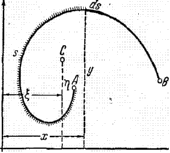
3). Пользуясь первой теоремой Гульдина, определить положение центра тяжести дуги (рис. 2) круга радиуса r.

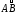
Так как эта дуга симметрична относительно радиуса ОМ, проходящего через ее середину М, то ее центр тяжести С лежит на этом радиусе, и для полного определения положения центра тяжести необходимо лишь найти его расстояние η от центра О. Выбираем оси, как указано на рисунке, и обозначим длину дуги через s, а ее хорды АВ (=А⁄В⁄) - через d. От вращения рассматриваемой дуги вокруг оси х получается шаравой пояс, площадь поверхности Р которого равна 2πrd.

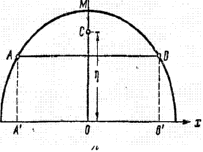
Рис.2

По теореме Гульдина, та же поверхность равна 2πηs, так что Sη = rd и

η = rd/s.

В частности, для полуокружности d = 2r, s = πr и η = 2r/π = 0,637r.

). В тех случаях, когда наперед ясно положение центра тяжести, теоремой Гульдина можно воспользоваться для определения площади поверхности вращения. Пусть, например, требуется определить величину поверхности кольца (тора), т.е. тела образованного вращением круга около оси, не пересекающей его (рис. 3).

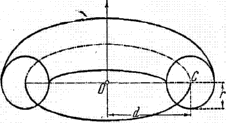
Рис.3

Так как очевидно, что центр тяжести окружности совпадает с ее центром, то (при обозначении рисунка) имеем P=2πr·2πd=4π2rd.

III. Нахождение статических моментов и центра тяжести плоской фигуры

Рассмотрим плоскую фигуру АА⁄В⁄В (рис. 4), ограниченную сверху кривой АВ, которая задана явным уравнением y = f(x). Предположим, что вдоль по этой фигуре равномерно распределены массы, так что поверхностная плотность их ρ (т.е. масса, приходящаяся на единицу площади) постоянна. Без существенного умаления общности можно тогда принять, что ρ = 1, т.е., что масса любой части нашей фигуры измеряется ее площадью. Это всегда и подразумевается, если говорят просто о статических моментах (или о центре тяжести) плоской фигуры.

Рис.4

Желая определить статические моменты Мх, Му этой фигуры относительно осей координат, мы выделим, как обычно, какой-нибудь элемент нашей фигуры в виде бесконечно узкой вертикальной полоски (рис. 4). Приняв эту полоску приближенно за прямоугольник, мы видим, что масса ее (выражаемая тем же числом, что и площадь) будет ydx. Для определения соответствующих элементарных моментов dМx, dМy предположим всю массу полоски сосредоточенной в ее центре тяжести (т.е. в центре прямоугольника), что, как известно, не изменяет величины статических моментов. Полученная материальная точка отстоит от оси х на расстоянии 0,5у, от оси y - на расстоянии (х + 0,5dx); последнее выражение можно заменить просто через х, ибо отброшенная величина 0,5dx, умноженная на массу ydx, дала бы бесконечно малую высшего порядка. Итак, имеем

, .

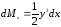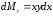Просуммировав эти элементарные моменты, придем к результатам

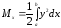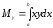, , (4)

причем под у разумеется функция f(x), фигурирующая в уравнении кривой АВ.

Как в случае кривой, по этим статическим моментам рассматриваемой фигуры относительно осей координат легко определить теперь и координаты ξ, η центра тяжести фигуры. Если через Р обозначить площадь (а следовательно, и массу) фигуры, то по основному свойству центра тяжести

, ,

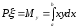откуда

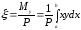, (5)

И в данном случае мы получаем важное геометрическое следствие из формулы для ординаты η центра тяжести. В самом деле, из этой формулы имеем

.

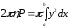Правая часть этого равенства выражает объем V тела, полученного от вращения плоской фигуры АА/ВВ/ около оси х, левая же часть выражает произведение площади этой фигуры Р на 2πη − длину окружности, описанной центром тяжести фигуры. Отсюда вторая теорема Гульдина.

Вторая теорема Гульдина:

Объем тела вращения плоской фигуры около не пересекающей ее оси равен произведению площади этой фигуры на длину окружности, описанной центром тяжести фигуры:

V=Ρ·2πη.

Заметим, что формулы (4), (5) распространяются на случай фигуры, ограниченной кривыми и снизу и сверху (криволинейная трапеция). Например, для этого случая

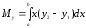, ; (4а)

отсюда ясно уже, как преобразуются формулы (5). Если вспомнить формулы

,

то легко усмотреть, что теорема Гульдина справедлива также и для этого случая.

Рассмотрим следующие примеры:

. Найти статические моменты Мх, Му и координаты центра тяжести фигуры, ограниченной параболой у2 = 2рх, осью х и ординатой, соответствующей абсциссе х.

Так как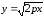, то по формулам (4)

, .

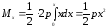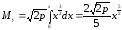С другой стороны, площадь 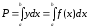, т.е.

.

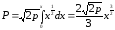В таком случае по формулам (5)

, .

Пользуясь значениями ξ и η, легко найти - по теореме Гульдина - объем тела вращения рассматриваемой фигуры вокруг осей координат или вокруг конечной координаты. Например, если остановиться на последнем случае, так как расстояние центра тяжести от оси вращения есть 2х/5, то искомый объем будет

.

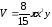. Если фигура имеет ось симметрии, то центр тяжести фигуры необходимо лежит на этой оси.

Докажем это для случая фигуры, ограниченной снизу и сверху кривыми y1 = f1(x) и y2 = f2(x). Если взять ось симметрии за ось y,то обе функции y1 и y2 окажутся четными; промежуток же изменения x в этом случае будет иметь вид [-а, а]. Тогда, по второй из формул (4а) ( Пусть f непрерывна в симметричном промежутке [-а; а] (а>0). Тогда в случае четной функции

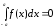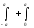, а в случае нечетной . В обоих случаях интеграл представляется в виде суммы интегралов и к первому из них применяется подстановка x= -t).

.

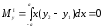Подобно первой теореме Гульдина и вторая теорема также может быть использована в том случае, когда положение центра тяжести ясно, для определения объема соответствующего тела вращения. Например, для тора (3) получается объем V= 2π2r2d.

Top (кольцо кругового сечения) r — радиус кругового сечения R —расстояние центра сечения от центра кольца	Поверхность тора	Объем тора
Шар R и D — радиус и диаметр шара	Поверхность шара, Sп	Объем шара