Bilety / 39

39. Геометрический смысл полного дифференциала ФДП. Касательная плоскость и нормаль к поверхности, их уравнения. Примеры.

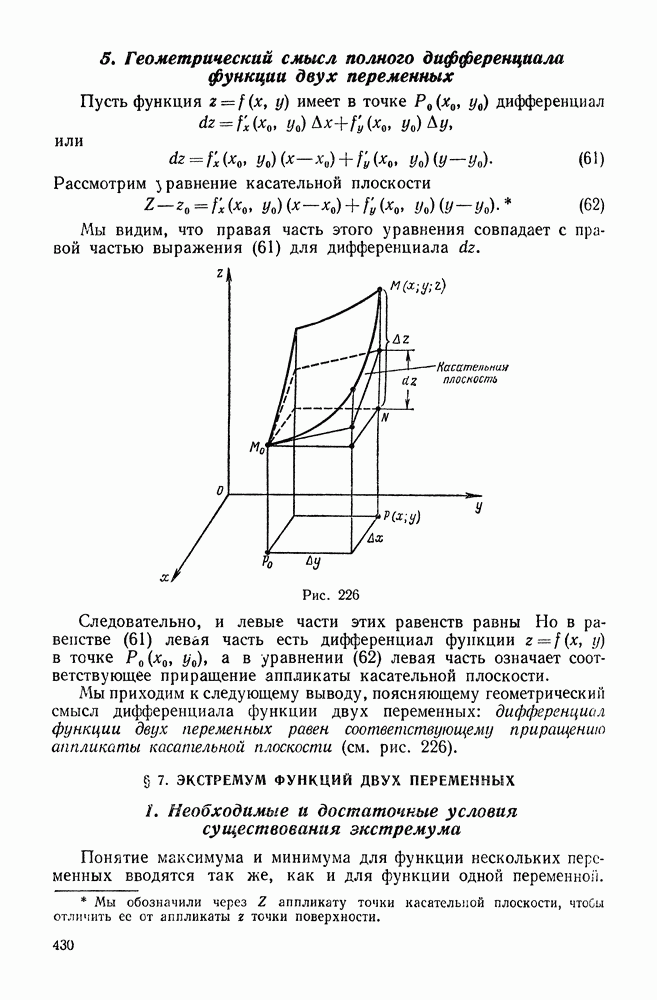
Задача № 7. Касательная плоскость и нормаль к поверхности.

Касательная плоскость к поверхности в её точке  (точка касания) есть плоскость, проходящая через и содержащая в себе все касательные, проведённые вточке  ко всевозможным кривым, проведённым на поверхности через точку 

Нормалью к поверхности в точке  называется прямая, проходящая через точку  и перпендикулярная к касательной плоскости, проведённой в этой точке.

Если уравнение поверхности имеет вид F(x, y, z)=0, то уравнение касательной плоскости в точке  имеет вид:

Уравнение нормали к этой поверхности в точке  есть

В случае явного задания поверхности уравнением (8.1) и (8.2) примут вид

Пример решений

Пример 7.1. Найти уравнение касательной плоскости и уравнение нормали к поверхности в точке 

Решение: Имеем

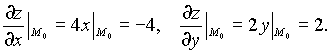
Тогда, согласно (8.3) уравнение касательной плоскости к данной поверхности в указанной точке будет иметь вид: z - 6 = - 4(x + 1) + 2(y - 2), то есть 4x - 2y + z + 2 = 0, а уравнение нормали

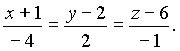
Пример 7.2. Найти уравнение касательной плоскости и нормали к косинусу

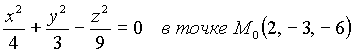
Решение. Имеем

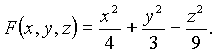
Тогда

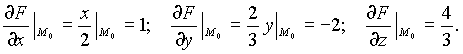
Уравнение касательной плоскости запишем в виде