36. Частные производные ФНП, их нахождение. Частные производные ФДП, их геометрический смысл. Примеры.

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.  Частные производные функции z(x,y) находятся по следующим формулам:  Вторые частные производные функции z(x,y) находятся по формулам:   

Смешанные частные производные функции z(x,y) находятся по формулам: 

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: – эточастное приращение функции z по аргументу x;  – это частное приращение функции z по аргументу у.  Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:   – это частная производная функции z по аргументу x;   – это частная производная функции z по аргументу у.  Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z = 2x⁵ + 3x²y + y² – 4x + 5y - 1

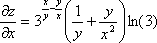
Пример 2. Найти частные производные  функции z = f(x;y) в точке A(x₀;y₀).    Находим частные производные:      Найдем частные производные в точке А(1;1)      Находим вторые частные производные:      Найдем смешанные частные производные: 

Геометрический смысл частных производных функции двух переменных

Остановимся на функции двух переменных.

Если каждой паре значений x, y из множества D ставится в соответствие одно определённое значение z из множества E, то z называется функцией двух независимых друг от друга переменных x и y и обозначается z= f(x, y).

Множество D называется областью определения функции z, а множество E – множеством её значений. Переменные x и y по отношению к функции z называются её аргументами.

Частным значениям аргументов

Соответствует частное значение функции

Пример 4.Область определения функции S = xy, выражающей зависимость площади многоугольника от длин его сторон, может быть записана двумя неравенствами

и

которые определяют I квадрант на плоскости xOy. Частное значение этой функции при x = 3, y = 5 составляет

В общем случае область определения функции двух переменных геометрически может быть представлена некоторым множеством точек (x; y) плоскости xOy.

Подобно тому, как функция y = f(x) геометрически изображается графиком, можно геометрически истолковать и уравнение z = f(x, y).

Ставя в соответствие каждой точке

аппликату z = f(x, y), мы получим некоторое множество точек (x; y; z) трёхмерного пространства – чаще всего некоторую поверхности. Поэтому равенство z = f(x, y) называют уравнением поверхности.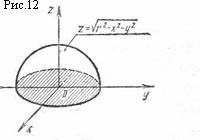

Пример 5. Пусть задана функция

Её область определения найдём из равенства

т.е.    

Это круг с центром в начале координат и радиусом r. Графиком функции

является верхняя половина сферы

(разрешив уравнение сферы относительно z, получим две однозначные функции z: и