Задача №1
Требуется определить статистические вероятности безотказной работы P(t) и отказа Q(t) устройства для заданного значения вероятности безотказной работы P*(t) по первым 20 значением наработки до отказа. Затем для заданной наработки t рассчитать математическое ожидание числа работоспособных устройств –Np(t) при общем числе находившихся в эксплуатации форсунок.
Значения
наработки устройства до отказа и заданные
значения
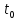 и
и
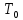 .
.
|
Вариант |
Массив
значений наработки до отказа T,
|
Заданное
значение t,
|
Значение
|
|
3 |
13,12,15,17,13,15,14,11,13,15,14,15,13,14,10,12,17,18,10,12,9,14,16,7,18,15,15,11,8,13,11,14,16,11,13,14,18,9,10,12,13,17,10,14,16,8,12,11,12,18 |
14,5 |
6,5 |
Объем партии устройств и заданное значение K
|
Вариант |
3 |
|
Объем партии |
300 |
|
Значение k |
5 |
Статистически вероятность безотказной работы устройства для наработки t определяется
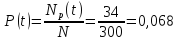
Вероятность отказа устройства за наработку t статистически определяется:

Проверка:

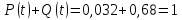
Оценка вероятности безотказной работы по первым 20 значениям наработки до отказа:
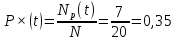
Математическое ожидание числа объектов к работе:
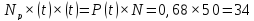
Задача№2
Требуется рассчитать среднюю наработку до отказа Т рассматриваемых форсунок. Первоначально вычисления произвести непосредственно по выборочным значениям Т, а затем с использованием статистического ряда.
Преобразование значений наработки до отказа в статистический ряд.
|
№ |
Интервал |
Число попаданий на интервал, n |
Статистическая вероятность |
|
1 |
6,5-9,5 |
5 |
0,1 |
|
2 |
9,5-12,5 |
15 |
0,3 |
|
3 |
12,5-15,5 |
20 |
0,4 |
|
4 |
15,5-18,5 |
10 |
0,2 |
Статистическая вероятность Q попадания случайной величины на i-ый интервал рассчитывается:
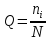
Средняя наработка до отказа:
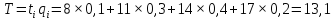
Среднее значение T случайной величины T непосредственно по выбранным значением t:

Оценка ошибки в расчетах:
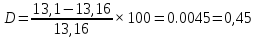
Задача №3
Требуется
рассчитать интенсивность отказов λ(t)
для заданных значений t
и
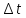 .
.
Интенсивность отказов λ(t) рассчитывается по формуле:
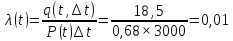
 то
наработка до отказа распределена по
экспоненциальному (показательному)
закону.
то
наработка до отказа распределена по
экспоненциальному (показательному)
закону.
В этом случае вероятность безотказной работы блока:
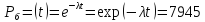
Вероятность безотказной работы подсистемы:
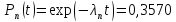
Средняя наработка блока до отказа:
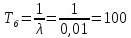
Интенсивность отказов подсистемы:

Наработка подсистемы до отказа:
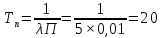
Задача №4
Для наработки t=T П требуется рассчитать вероятность безотказной работы Рс(Т П) системы (рис.3) состоящий из двух подсистем, одна из которых является резервной.
Вероятность отказа одной подсистемы:
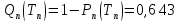
Вероятность отказа всей системы:
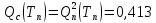
Вероятность безотказной работы системы:
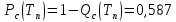
или иначе:

Задача №5
Требуется определить зависимости от наработки (пробега автомобиля) математического ожидания (среднего значения) износа шатунных шеек коленчатого вала ДВС –y(t) и дисперсии износа Д(у(t)), полученные уравнения необходимо записать. Параметры искомых зависимостей следует рассчитать с использованием правила определения уравнения прямой, проходящей через две точки с известными координатами.
Результаты обработки измерения износа шатунных шеек коленчатых валов двигателя автомобиля.
|
Расчетная величина |
Первое измерение |
|
Пробег
|
50 |
|
Средний
износ
|
0,090 |
|
Дисперсия
износа Д( |
0,157 |
|
|
Второе измерение |
|
Пробег
|
115 |
|
Средний
износу |
0,174 |
|
Дисперсия
износа Д( |
0,251 |
Линейные функции для описания зависимости износа от пробега автомобиля:
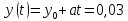

Параметры зависимости а и b:
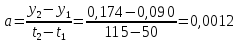
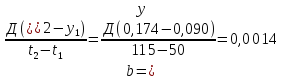
Параметры
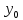 и Д(
и Д(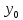 ):
):
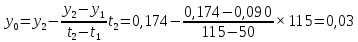

Находим
y(t)
и Д(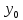 ):
):
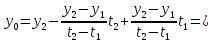
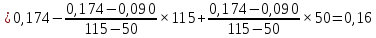
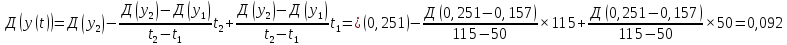


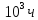
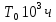
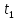 ,
тыс.км
,
тыс.км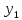 ,мм
,мм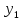 ),
),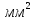
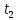 ,
тыс.км
,
тыс.км ,мм
,мм ),
),