
pervajalekcijafizikamatemdljalechfaka
.pdf
ФУНКЦИЯ ОДНОГО ПЕРЕМЕННОГО.
Понятие функции
Понятие функции связано с установлением зависимости между элементами двух множеств. Пример: А – множество натуральных чисел, а В – множество квадратов натуральных чисел или А – множество треугольников, а В – множество периметров этих треугольников.
Если каждому элементу х множества Х по определенному правилу можно поставить в соответствие одно или несколько значений элемента у множества У, то говорят, что задана
функция y от x ( |
y f (x) |
), где f есть некоторое |
|
правило, х носит название аргумента функции, а у – значения функции.
Совокупность значений x для которых правило вычисления значений y имеет смысл, называется областью определения функции или областью существования функции, а
область изменения У называется множеством значений функции.
Способы задания функции.
1. Табличный способ задания функции.
При этом способе выписываются в определенном порядке значения аргумента и соответствующие значения функции.
х |
х1 |
х2 |
… |
Хn |
y |
Y1 |
Y2 |
… |
yn |
Примером таких таблиц могут служить таблицы тригонометрических функций, таблицы логарифмов, результаты экспериментов.
2. Графический способ задания функции.
Если в прямоугольной системе координат на плоскости изобразить в виде линии некоторую совокупность точек
так, что y f (x) , где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется
графиком функции.
Откладывая на оси абсцисс необходимое значение x и восстанавливая перпендикуляр из точки x до пересечения
с кривой, а затем, проводя прямую, параллельную оси абсцисс до пересечения ее с осью
ординат, получим значение функции |
y f (x) |
в точке x. |
|
|
|
||
3. Аналитический способ задания функции. |
|
|
|
При аналитическом способе задания |
функция представляется аналитическим |
||
выражением, то есть через совокупность известных математических операций, которые производятся в определенной последовательности над числами и символами. Пример:
|
у x3 |
5 , |
у lg x cos x . |
|
|
|
|
||
|
Элементарные функции. Свойства функций. |
|
|
||||||
|
|
|
|
|
|
|
|
||
№ |
Обозна- |
Область |
Область |
Четность, |
Монотон- |
Перио- |
|
||
чение |
опреде- |
значений |
нечет- |
Графики функций |
|||||
п/п |
ность |
дичность |
|||||||
функ- |
ления Х |
У |
ность |
|
|||||
|
|
|
|
||||||
1
1
1
2
3
ции |
|
|
|
|
2 |
3 |
4 |
5 |
6 |
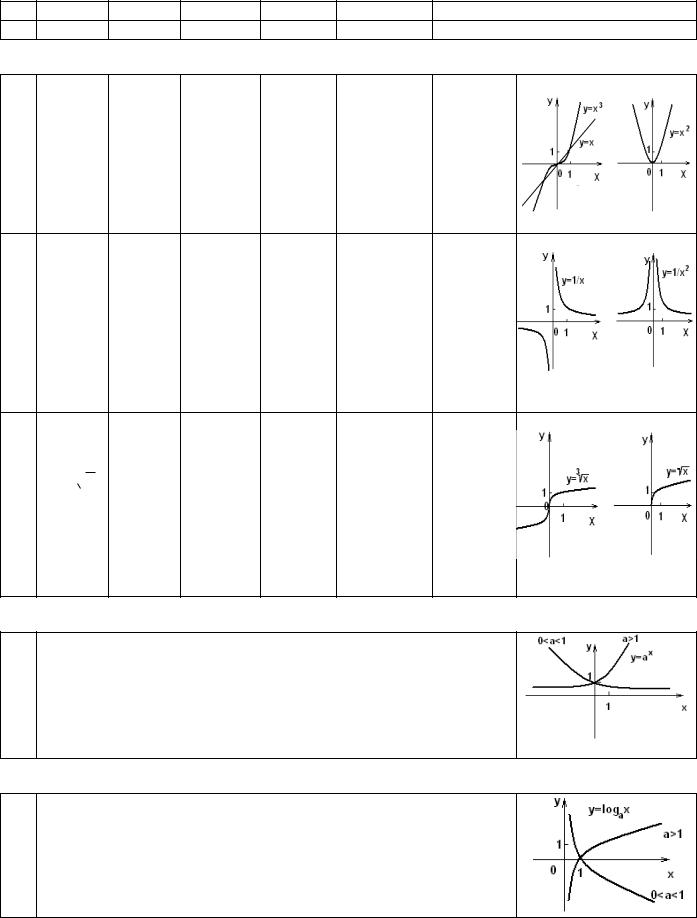
1. Степенная функция
у х n n N
ух n n N
уn х n N n 1
х n N n 1
( , )
( ,0)(0, )
( , ) ,
если n – нечетно;
0, ,
если n - четно
|
|
|
Возрастает на |
|
( , ) , |
|
Нечетная, ( , ) , если |
||
если n – |
|
если n – |
n – нечетно. |
|
|
нечетно; |
|||
нечетно; |
Убывает на |
|||
|
||||
0, , |
|
четная, |
,0 и |
|
если n - |
возрастает на |
|||
если n - |
||||
четно |
|
(0, ) , если n |
||
|
четно |
|||
|
|
|
||
|
|
|
– четно. |
|
|
|
|
Убывает на |
|
( ,0) |
, |
Нечетная, |
( ,0) и на |
|
|
(0, ) , если |
|||
(0, ) |
если n – |
|||
|
||||
если n – |
|
нечетно; |
n – нечетно. |
|
нечетно; |
|
Возрастает |
||
0, , |
|
четная, |
на ( ,0) и |
|
если n - |
если n - |
убывает на |
||
четно |
|
четно |
(0, ) , если |
|
|
|
|
n – четно. |
|
( , ) ,
если n – нечетно;
0, ,
если n - четно
Нечетная, если n – нечетно; не является четной или нечетной, если n - четно
Возрастает
на ( , ) ,
если n – нечетно.
Возрастает на0, , если n – четно.
2. Показательная функция
7 |
8 |
Непериодическая
Непериодическая
Непериодическая
4
5
|
|
|
|
|
|
Не |
|
Возрастает |
|
||
у а |
х |
|
|
|
|
|
на ( , |
) , |
|
||
|
|
|
|
является |
|
|
|||||
|
|
|
|
|
|
если |
а>1 и |
Неперио- |
|||
|
|
|
|
( , ) |
(0, ) |
|
|||||
а 0, |
|
|
четной |
|
|||||||
|
|
|
убывает |
на |
дическая |
||||||
а 1 |
|
|
|
|
|
или |
|
||||
|
|
|
|
|
|
( , ) , |
|
|
|||
|
|
|
|
|
нечетной |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
если 0<a<1. |
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
3. Логарифмическая функция |
|
|
|
|
|
||||||
|
|
|
|
|
|
Не |
|
Возрастает |
|
||
|
|
|
|
|
|
|
|
||||
у log |
|
x |
|
|
|
на |
(0, ) , |
|
|||
a |
|
|
является |
|
если |
а>1 и |
Неперио- |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
a 0, |
|
|
|
(0, ) |
( , ) |
четной |
|
||||
|
|
|
|
убывает |
на |
дическая |
|||||
a 1 |
|
|
|
|
|
или |
|
||||
|
|
|
|
|
|
(0, ) , если |
|
||||
|
|
|
|
|
нечетной |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0<a<1 . |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
4.Тригонометрические функции |
|
|
|
|
|
||||||
2
1
6
7
2
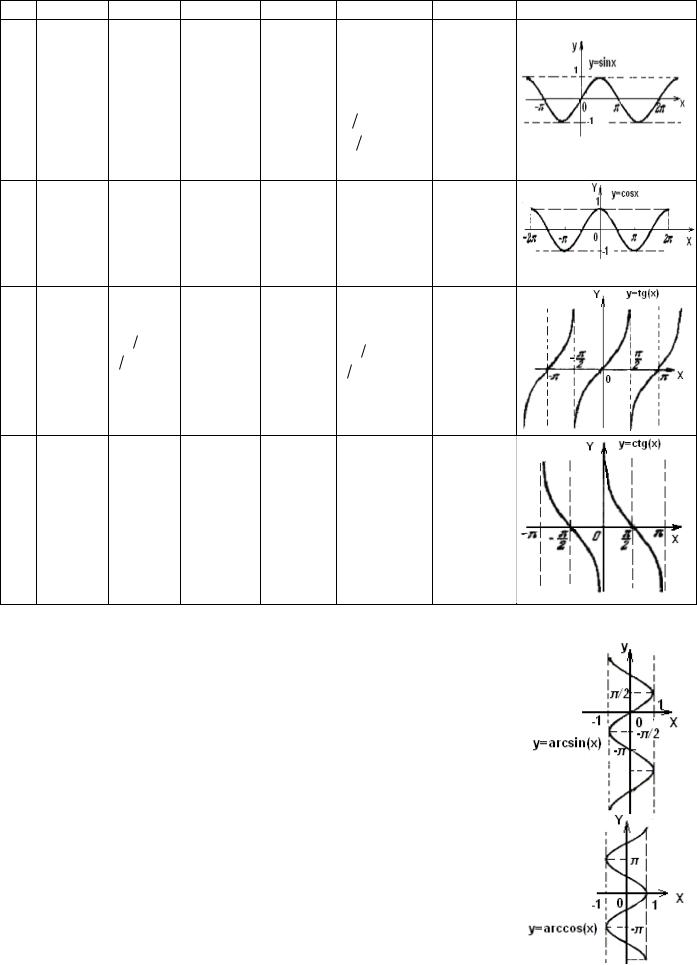
уsin(x)
уcos(x)
3
( , )
( , )
4
[-1, 1]
[-1, 1]
5 6
Возрастает на
[ 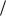 2 2 n,
2 2 n,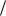 2 2 n].
2 2 n].
Нечетная Убывает на
[ |
2 2 n, |
3 |
2 2 n], |
n Z |
|
7 |
8 |
Период
T 2
|
Возрастает на |
|
|
[ 2 n,2 n]. |
Период |
Четная |
Убывает на |
|
|
[2 n, 2 n], |
T 2 |
|
|
|
|
n Z |
|
8 |
у tg(x) |
9 у сtg (x)
( |
2 n, |
2 n), |
|
n Z |
|
( n, n), n Z
( , )
( , )
Нечетная
Нечетная
Возрастает на
( |
2 n, |
2 n), |
|
n Z |
|
Убывает на
[ n, n], n Z
Период
T
Период
T
5. Обратные тригонометрические функции
|
|
|
|
Не |
|
|
|
|
|
|
|
( , ) |
является |
Функция не |
Функция не |
|
|
10 |
у arcsin x |
[-1, 1] |
четной |
|
|
|||
однозначна |
однозначна |
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
или |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
нечетной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не |
|
|
|
|
|
|
|
( , ) |
является |
Функция не |
Функция не |
|
|
11 |
у arccos x |
[-1, 1] |
четной |
|
|
|||
однозначна |
однозначна |
|
|
|||||
|
|
|
|
или |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
нечетной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
1
12
2
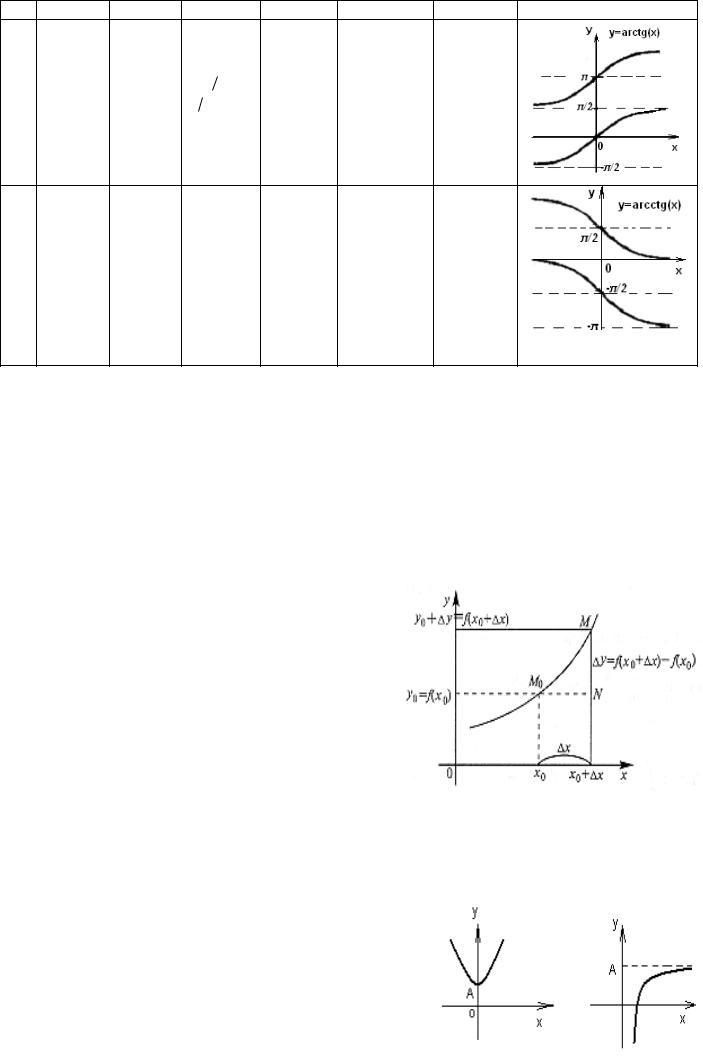
у arctgx
3
( , )
4
( |
2 n, |
2 n), |
|
n Z |
|
5 |
6 |
7 |
8 |
Не является Функция не Функция не
четной однозначна однозначна или
нечетной
13 Y=arcctgx
( , )
|
Не |
|
|
[ n, n], является |
Функция не Функция не |
||
n Z |
четной |
||
однозначна однозначна |
|||
|
или |
||
|
|
||
|
нечетной |
|
|
Функция |
y f (x |
выполняется равенство f ( x) f (x) .
) f
называется
( x) f (x)
четной, если для всех допустимых значений х и называется нечетной, если выполняется правило
Функция |
y f (x) , называется периодической, если существует такое постоянное |
число Т, при прибавлении или вычитании которого от аргумента значение функции не меняется, т.е. f (x T ) f (x) , f (x T ) f (x) . Наименьшее такое число Т называется периодом функции.
Функция называется возрастающей на интервале, если большему значению аргумента из этого интервала соответствует большее значение функции, то есть при ∆Х>0
имеем ∆У>0, где ∆Х |
называется |
||
приращением |
аргумента функции и |
||
определяется |
как |
разность |
между |
последующим |
и предыдущим |
значением |
|
аргумента х х х0 , |
а ∆У |
называется |
|
приращением функции и находится как разность у f (х) f (х0 ) f (x0 x) f (x0 ) .
Функция называется убывающей на интервале, если большему значению аргумента из этого интервала соответствует меньшее значение функции, то есть при ∆Х>0 приращение функции ∆У<0.
Предел функции.
Говорят, что функция у=f(x) имеет предел А при х→а, если при приближении х к а значение

функции как угодно близко подходит к А, то есть
A lim х a
f
(x)
.
Для
A lim x
первого графика, изображенного на рисунке,
у(x) .
A lim x 0
у(x)
, а для второго
Вычисление пределов.
Для вычисления пределов используют основные теоремы и правило Лопиталя (при возникновении «неопределенности» вида 0/0 или ∞∕∞), согласно которому предел частного двух функций равен пределу отношений производных этих функций:
lim |
(x) |
|
(x) |
||
x a |
lim |
(x) |
|
(x) |
||
x a |
, при условии, что этот предел существует. Если после использования
этого правила снова возникает неопределенность, то его применяют вторично.
Пример:
Решение:
Найти предел функции:
lim(x |
2 |
7x 4) lim(x |
2 |
) |
|
|
|||
x 3 |
|
x 3 |
|
|
lim(x |
2 |
7x |
|
||
x 3 |
|
|
7 lim(x) 4 |
||
x 3 |
|
|
4) .
8 .
Пример: Найти предел функции:
lim x 0
sin(2x) x
.
Решение: При подстановке х=0 получаем неопределенность 0/0. Тогда по правилу
Лопиталя:
lim |
sin(2x) |
lim |
(sin(2x)) |
lim |
2 cos(2x) |
|
x |
(x) |
1 |
||||
x 0 |
x 0 |
x 0 |
2 lim cos(2x) x 0
2
.
Непрерывность функции.
Большинство функций, изучаемых в математическом анализе, являются непрерывными, то есть при небольших изменениях аргумента х функция у меняется также мало, и график такой функции является непрерывной кривой. Однако, у некоторых функций при определенных значениях х непрерывность может нарушаться и график прерываться, тогда говорят, что функция в данных точках имеет разрыв. Значения аргумента, при которых происходит разрыв функции, называются точками разрыва.
Функция y=f(x) непрерывна в точке x0, если в этой точке у нее существует предел
lim f (x) f (x0 ) .
x x0
Функция у=f(x) называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Сложная функция.
Пусть заданы две функции у g(х) |
и z f ( y) , причем область определения |
функции f содержит множество значений функции g. В этом случае функция z f (g(x)) называется сложной функцией, составленной из функций g и f.
5

Подобным образом можно рассматривать сложные функции, составленные из более чем двух функций.
Пример:
у
log |
3 |
(sin |
|
|
x)
,
у
у
|
2x |
|
|
arccos |
x |
2 |
|
1 |
|
||
|
|
|
|
x lg( 2x 3) |
|||
,
.
ФУНКЦИЯ НЕСКОЛЬКИХ АРГУМЕНТОВ.
Понятие функции двух переменных
Функция не всегда зависит от одной переменной. Например, объем прямоугольного параллелепипеда зависит от длины его трех взаимно перпендикулярных ребер ( V x y z ), то есть является функцией трех переменных, а площадь прямоугольного треугольника
зависит от длины двух его катетов
(
S
1 2
x
y
), то есть является функцией двух
переменных.
Если каждой упорядоченной паре чисел (х, у), таких, что х принадлежит множеству Х, а у – множеству У, по определенному правилу поставлено в соответствие одно или несколько чисел z, где z принадлежит множеству Z, то говорят, что задана функция двух независимых переменных z=f(x,y).
При этом число z называют значением функции f в точке (х,у), переменные х и у –
независимыми аргументами функции, множество (х, у) - областью определения
функции, а множество Z – множеством значений функции.
Пример: Найти область определения функции |
z |
x y |
|
2x y |
|||
|
|
||
Решение. |
|
|
.
Выражение, стоящее справа, теряет смысл при тех значениях х и у, при которых знаменатель обращается в нуль. Отсюда областью определения функции является вся плоскость, из которой выброшена прямая у=2х.
Функция двух переменных изображается в пространстве в виде поверхности, которая определяется множеством точек (х,у,z), где z является зависимой переменной и находится по формуле z=f(x,y).
Пример:
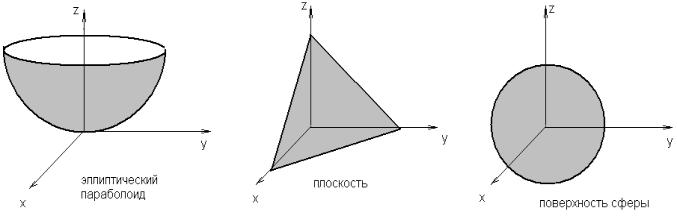
z x2 y 2 - эллиптический параболоид (см. рисунок),
z x 4y 8 - плоскость,
6
z |
2 |
x |
2 |
y |
2 |
9 |
|
|
|
|
- поверхность сферы.
Таким образом, сама формула, задающая функцию, и есть уравнение поверхности.
Так как построение графиков функции нескольких переменных в большинстве случаев представляет значительные трудности, то основным способом задания функции нескольких аргументов является аналитический способ.
Частное и полное приращение функции двух переменных.
Частным приращением
|
х |
z |
|
|
функции Z=f(x,y) по ее аргументу х называется
приращение, которое получает эта функция, аргумент у остается неизменным: х z f (x
если ее аргумент х имеет приращение ∆х, а
x, y) f (x, y) .
Частным приращением
|
y |
z |
|
|
функции Z=f(x,y) по ее аргументу у называется
приращение, которое получает эта функция, аргумент х остается неизменным: y z f (x,
если ее
y y)
аргумент у имеет приращение ∆у, а f (x, y) .
Полным приращением
|
z |
функции Z=f(x,y) по ее аргументам х и у называется
приращение, которое получает эта функция, если оба ее аргумента получают приращения:
z f (x x, y у) f (x, y) . |
|
|
|
|
|
|
|
ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. |
|||||||
Понятие производной функции |
|
|
|
|
|
|
|
Производной функции |
y f (x) |
в точке х0 |
|
называется |
предел при х 0 |
||
отношения приращения |
функции в |
этой точке |
к |
приращению аргумента (при |
|||
условии, что этот предел существует), то есть у |
|
f |
|
f |
. |
||
|
(x) lim |
x |
|||||
|
|
|
|
|
х 0 |
|
|
Нахождение производной называется дифференцированием функции. Необходимым
условием дифференцируемости функции является ее непрерывность.
7

Находить производную функции, используя ее определение, слишком сложно, поэтому были разработаны формулы и правила дифференцирования.
Формулы дифференцирования
1) |
(c) |
|
0 |
|
2) |
(x) 1 |
||||
|
|
|
|
|
|
3) |
(x |
n |
) |
|
|
|
|||||
|
|
||||
4) |
(ln x) |
||||
5) |
(loga |
x) |
|||
;
;
n
1 x
x |
n 1 |
|
;
1 |
|
|
ln a |
||
|
;
1 x
;
6) |
(a |
x |
) |
|
a |
x |
ln a ; |
||||
|
|
|
|||||||||
7) |
(e |
x |
) |
|
e |
x |
; |
|
|
||
|
|
|
|||||||||
|
|
|
|
|
|||||||
8) |
(sin x) |
|
cos x ; |
||||||||
|
|||||||||||
9) |
(cos x) sin x ; |
||||||||||
10) (tg x) |
|
1 |
; |
||||||||
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
cos |
x |
||
|
|
|
|
|
|
|
|
|
|||
11) |
(ctg x) |
1 |
|
|
; |
|
|
|
|
||||
|
2 |
x |
|
|
|
|
|||||||
|
|
|
|
sin |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
12) |
(arcsin x) |
|
|
1 |
|
|
; |
|
|
||||
1 x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
13) (arccos x) |
|
|
|
1 |
|
|
|
; |
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
1 x2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
14) |
|
(arctg x) |
|
|
|
1 |
|
|
; |
|
|
|
|
|
1 x |
2 |
|
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15) |
(arcctg x) |
|
1 |
|
. |
|
|
|
|||||
x |
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Правила дифференцирования
1.Производная алгебраической суммы (или разности) дифференцируемых функций равна алгебраической сумме (или разности) производных этих функций:
|
|
|
|
(u v w) |
u |
v |
w . |
2. Постоянный множитель можно выносить за знак производной:
(С
f (x)) C
f
(x)
.
3.Производная произведения двух функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую:
(u v) u v
v u
.
4.Производная частного двух функций равна дроби, числитель которой равен разности произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя исходной дроби:
u |
|
|
u |
|
|
|
||
|
|
|
v v u |
. |
||||
|
|
|
|
|
|
|
||
|
|
|
|
v2 |
||||
v |
|
|
|
|
|
|||
5.Производная сложной функции. Если функция u= (x) имеет производную в точке xo , а функция y=f(u) имеет производную в соответствующей точке uо= (xo), то сложная функция у=f [ (x)] дифференцируема в точке xo и справедлива следующая формула:
y (x0 ) f (u0 ) (x0 ) .
Таким образом, при нахождении производной сложной функции необходимо ввести промежуточный аргумент u= (x), позволяющий свести данную функцию к виду основных элементарных функций у= f [ (x)]=f(u), взять производную этой функции, а затем умножить ее на производную от промежуточного аргумента u.
Пример: Найти производную функции y=3x 2 +ln(x)+4
Решение: y (3x2 ln x 4) 3(x2 ) 1x 0 6x 1x
8

Сначала воспользовались формулой для производной суммы функций: (u
Затем вынесли постоянный множитель 3 за знак производной |
(3x |
2 |
|
3(x |
2 |
|
) |
|
)
v)
.
u
v
.
|
|
|
|
2 1 |
|
Из таблицы производных нашли (x |
2 |
) |
2x |
2x и (ln x) |
|
|
|
И, наконец, учли, что производная константы равна нулю
|
1 |
. |
|
x |
|||
|
|
||
|
|
0 . |
|
(4) |
|||
Пример: Найти производную функции
y sin(3x |
2 |
|
1)
.
Решение:
y |
cos(3x |
2 |
1) |
6x |
|
||||
x |
|
|
|
|
Сложную функцию y sin(3x2 1) представили как y sin , где (3x2 1) . Тем самым мы привели ее к виду основных элементарных функций. По формуле производной
сложной |
|
|
|
|
функции |
|
|
записали: |
|
|
|
|
|
2 |
|
cos 6x cos(3x |
2 |
1) |
6x . |
yx |
y x |
(sin ) (3x |
|
1)x |
|
||||
Физический и геометрический смысл производной.
Физический смысл производной - скорость протекания процесса в данной точке или мгновенная скорость изменения функции в данной точке.
Пример: Развитие патологического процесса со временем описывается уравнением
y t |
3 |
t |
2 |
1. Найти его скорость через 2 секунды от начала развития. |
||||||||||||||
|
|
|||||||||||||||||
Решение: |
Скорость развития патологического процесса, |
есть производная от функции, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
t |
2 |
1) |
|
|
3t |
2 |
2t . |
|
описывающей этот процесс: v(t) y (t) (t |
|
|
|
|
||||||||||||||
Мгновенная скорость через 2 секунды: |
|
|
|
3 2 |
2 |
2 |
2 12 4 8 . |
|||||||||||
y (2) |
|
|||||||||||||||||
Геометрический смысл производной - |
направление процесса в данной точке. |
|||||||||||||||||
Докажем это с помощью графика непрерывной |
|
|
|
|
|
|
||||||||||||
функции y=f(x), представленного на рисунке. |
|
|
|
|
|
|
||||||||||||
Возьмем |
|
любое |
значение |
переменной |
х0 . Ему |
|
|
|
|
|
|
|||||||
будет соответствовать значение функции |
f( |
х0 ). |
|
|
|
|
|
|
||||||||||
Аргументу х0 |
зададим приращение |
x. |
В точке |
|
|
|
|
|
|
|||||||||
х0 х |
|
функция имеет |
значение |
f( х0 х ). |
|
|
|
|
|
|
||||||||
Приращению |
|
аргумента |
x |
соответствует |
|
|
|
|
|
|
||||||||
приращение |
функции |
y=f( х0 х )-f( |
х0 ). |
|
|
|
|
|
|
|||||||||
Отношение y/ x очевидно есть тангенс угла |
|
|
|
|
|
|
||||||||||||
( x). |
|
|
При |
x 0, секущая |
MN примет |
|
|
|
|
|
|
|||||||
положение касательной к графику функции y=f(x) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |

в точке М, а угол ( x) - значение угла 0 - |
угла между касательной, проведенной к |
графику функции y=f(x) в точке с координатами |
( х0 , f( х0 )) и осью абсцисс. |
Таким образом, производная функции в какой-либо точке
х |
0 |
|
численно равна
тангенсу угла наклона касательной, проведенной к графику функции y=f(x) в этой точке х0 , и осью абсцисс.
Отсюда следует важный практический вывод: чтобы найти мгновенную скорость изменения одной величины при изменении другой при заданном значении аргумента, достаточно найти тангенс угла наклона касательной, проведенной к графику функции при данном значении ее аргумента.
Физический смысл второй производной – ускорение процесса в данной точке.
ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ АРГУМЕНТОВ.
Понятие частной производной функции
Частной производной функции z=f(x,у) по аргументу х в точке (х0,у0) называется предел отношения частного приращения х z функции к соответствующему приращению
ее аргумента |
∆х при стремлении |
последнего к |
нулю |
|
при условии, что этот предел |
||||||||||||
|
|
|
z |
lim |
|
|
z |
lim |
f (x x, y |
|
) f (x |
, y |
|
) |
|
||
существует: |
zx |
|
|
х |
|
0 |
|
0 |
|
0 |
|
0 |
|
. |
|||
x |
x |
|
x |
|
|
|
|
||||||||||
|
|
|
x 0 |
x 0 |
|
|
|
|
|
|
|||||||
Частной производной функции z=f(x,у) по аргументу у в точке (х0,у0) называется
предел отношения частного приращения |
у z функции к соответствующему приращению |
||||||||||||
ее аргумента ∆у при стремлении |
последнего к |
нулю |
при условии, что этот предел |
||||||||||
существует: z y |
z |
lim |
y z |
lim |
f (x |
, y |
0 |
y) f (x |
, y |
0 |
) |
|
|
|
|
0 |
|
|
0 |
|
|
. |
|||||
y |
y |
|
|
|
y |
|
|
|
|
||||
|
y 0 |
y 0 |
|
|
|
|
|
|
|
|
|||
Частная производная функции нескольких переменных по какому-либо из ее аргументов характеризует скорость изменения данной функции при изменении этого аргумента.
Вычисление частных производных функции
Частные производные функции нескольких переменных находят, используя те же правила и формулы, что и для нахождения производных функции одной переменной, однако при нахождении частной производной функции нескольких переменных по какому-либо аргументу все остальные аргументы этой функции считают постоянными величинами.
Пример: Найти частные производные функции z 
 xy
xy
10
