§4.3. Многокритериальный выбор альтернатив на основе пересечения нечетких множеств

Пусть имеется множество альтернатив и множество критериев, при этом оценки альтернатив по каждому-му критерию представлены нечеткими множествами, которые будем записывать в виде.

Правило выбора лучшей альтернативы можно представить как пересечение нечетких множеств, соответствующих критериям: . Функция принадлежности нечеткого множестваимеет вид. Лучшей считается альтернатива, имеющая наибольшее значение функции принадлежности. Если критерииимеет различную важность, то их вклад в общее решение можно представить как взвешенное пересечение:, где- весовые коэффициенты соответствующих критериев, которые должны удовлетворять следующим условиям: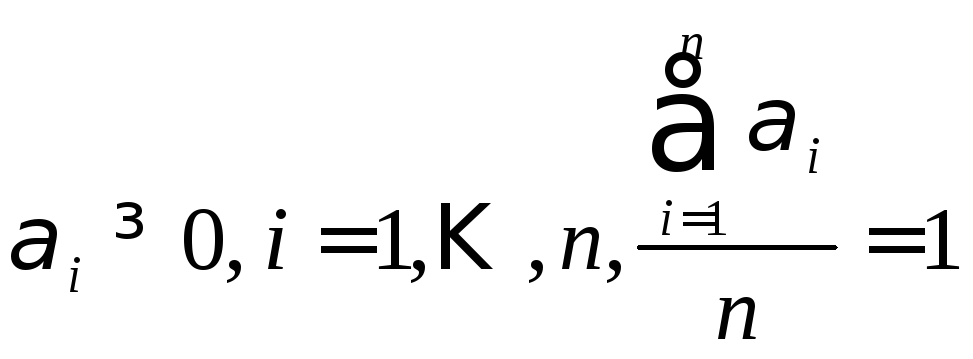. Коэффициенты относительной важностиможно определить, используя процедуру попарного сравнения критериев.

Пример. Цель решаемой задачи – выбор лучшего банка для размещения денежных средств физическим лицом. Было выбрано три банка: альтернативы . Определено шесть критериев выбора:- процентная ставка;- расположение банка;- активы банка;- политика банка;- ликвидность банка;- репутация банка (оценивается по экспертной пятибалльной шкале). Значения критериев для всех альтернатив определены ниже.

Критерии	Альтернативы
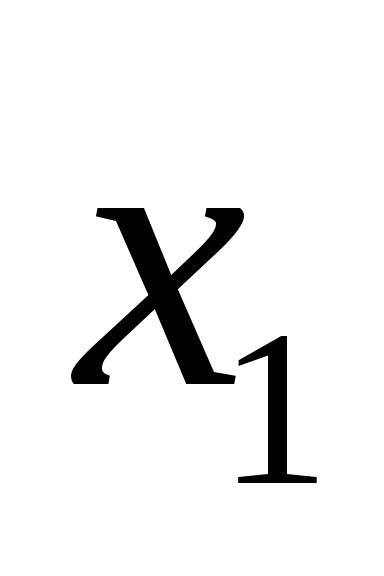
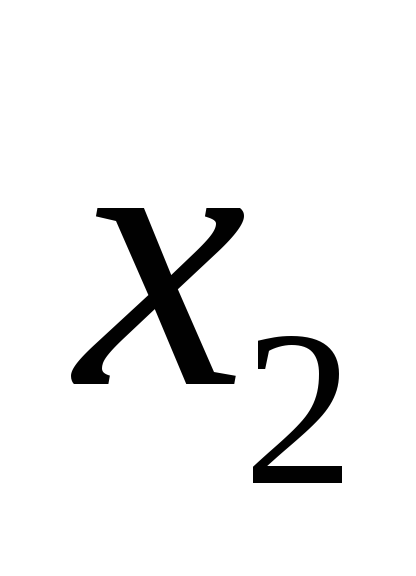
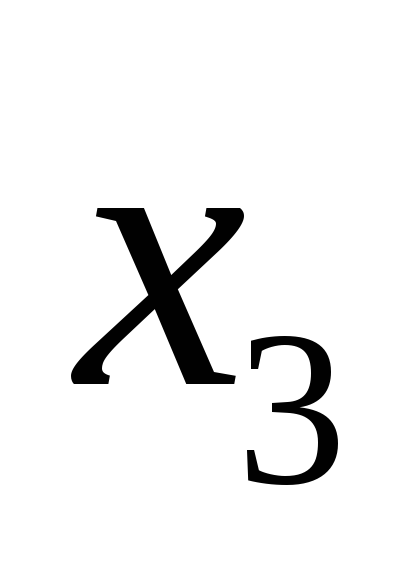
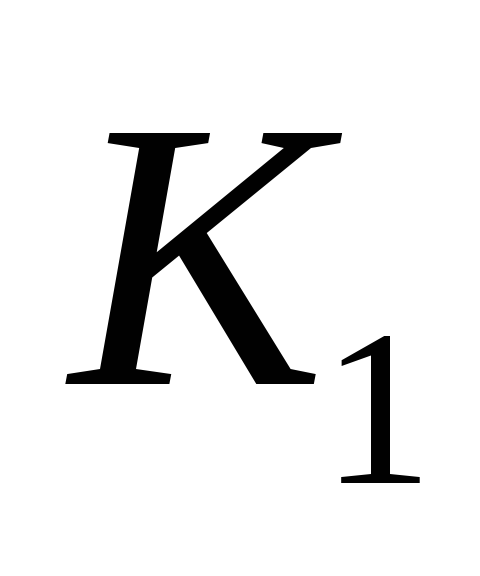
	30	35	40
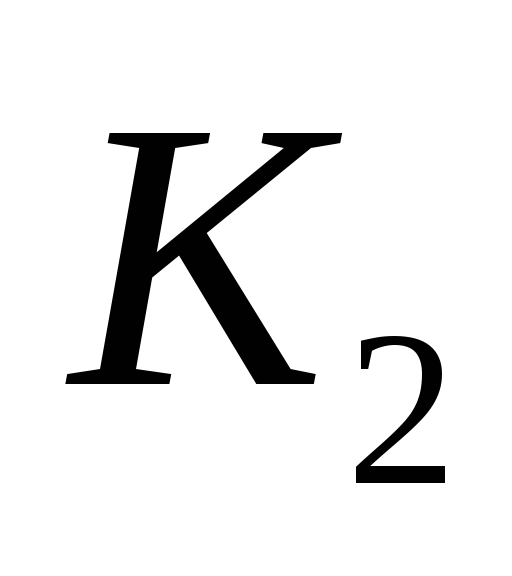
	Рядом с домом	В одном районе	В одном городе
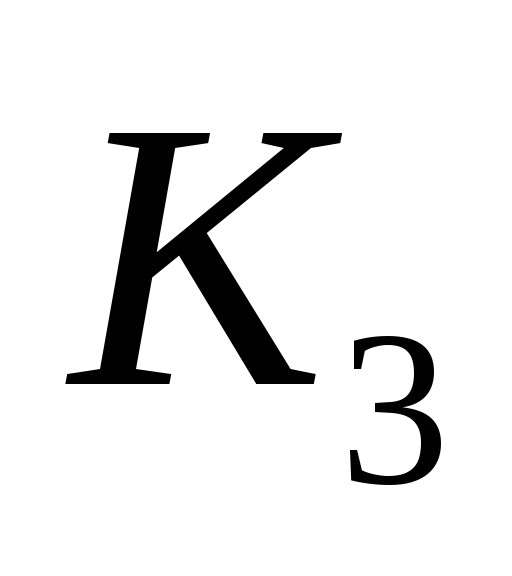
	15	20	10
	Консервативная	Умеренная	Рискованная
	2	2,5	1,5
	5	4	3

Все критерии представлены следующими нечеткими множествами:

;

;

;

;

;

.

Критерии имеют различную значимость при определении наиболее рационального варианта. В связи с этим необходимо определить весовые коэффициенты критериев.

Один из возможных способов получения значений весовых коэффициентов заключается в построении матрицы попарных сравнений критериев. Для критериев, использованных при решении задачи выбора лучшего банка, составлена следующая матрица попарных сравнений критериев.

Выбор банка
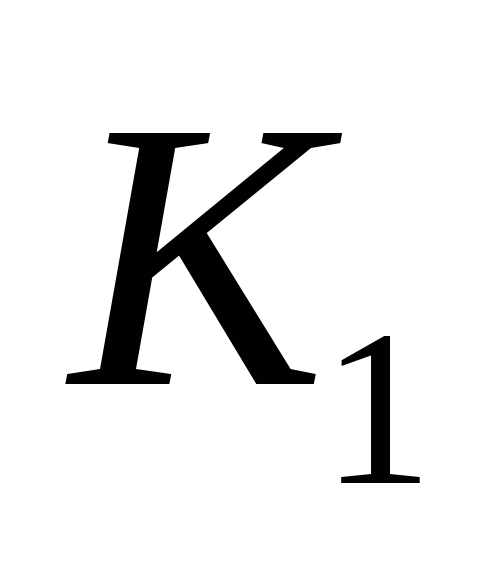
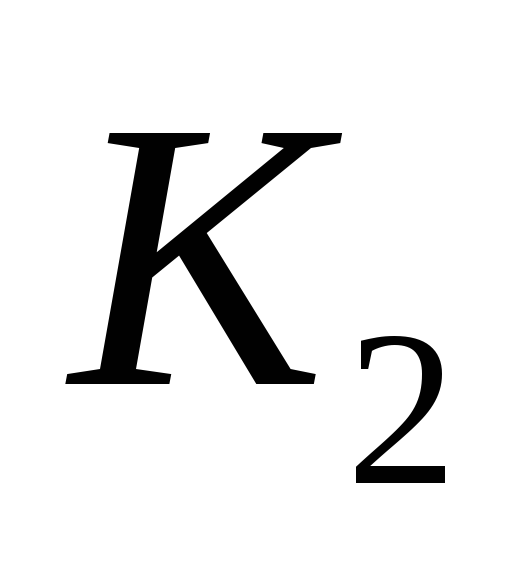
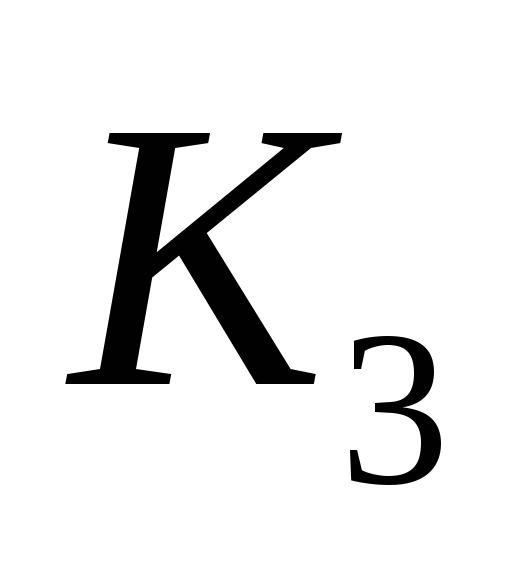
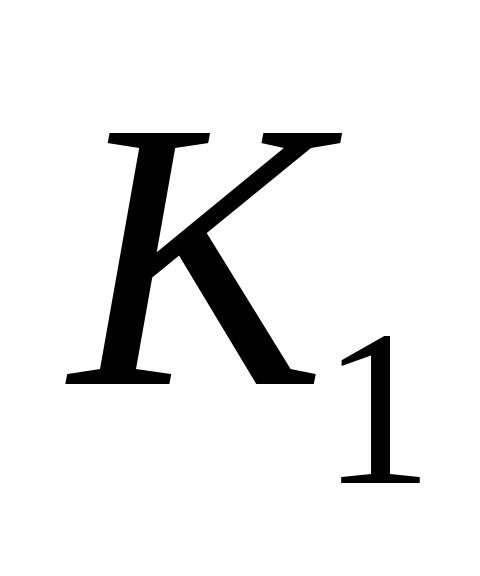
	1	7	3	4
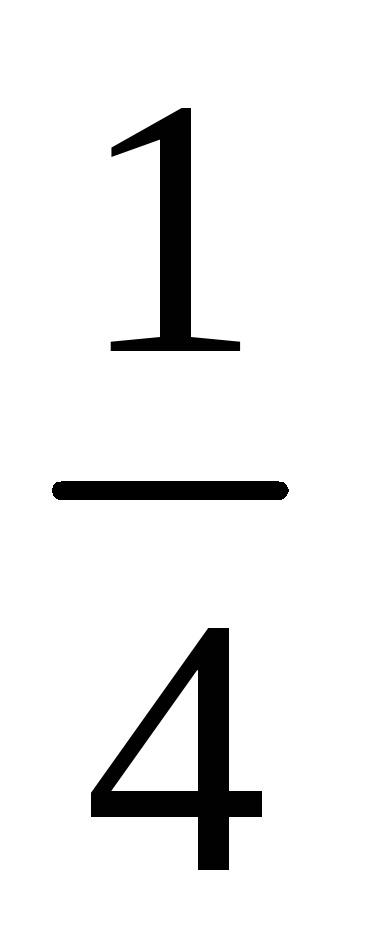
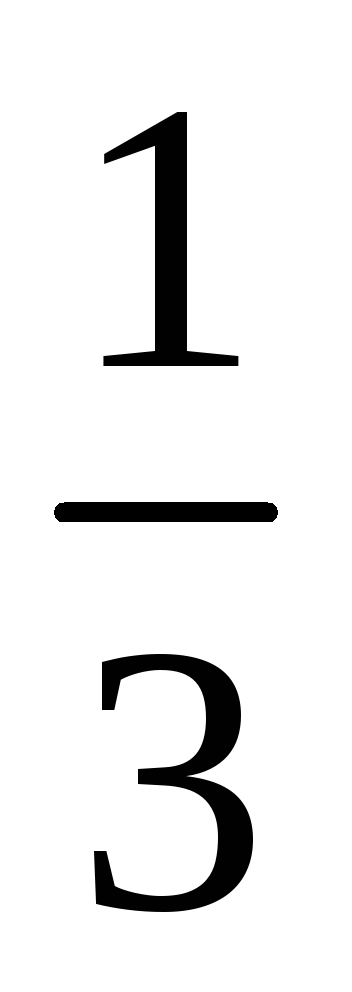
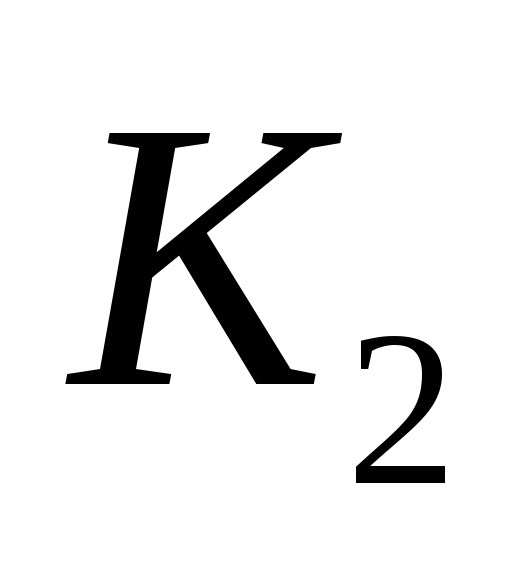
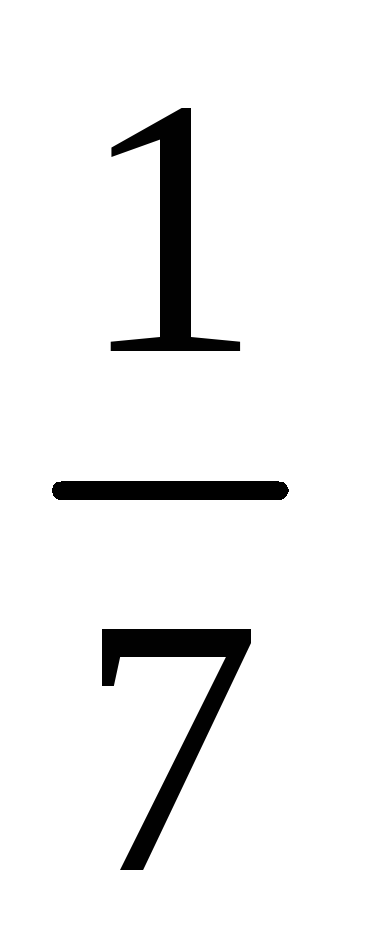
		1	1
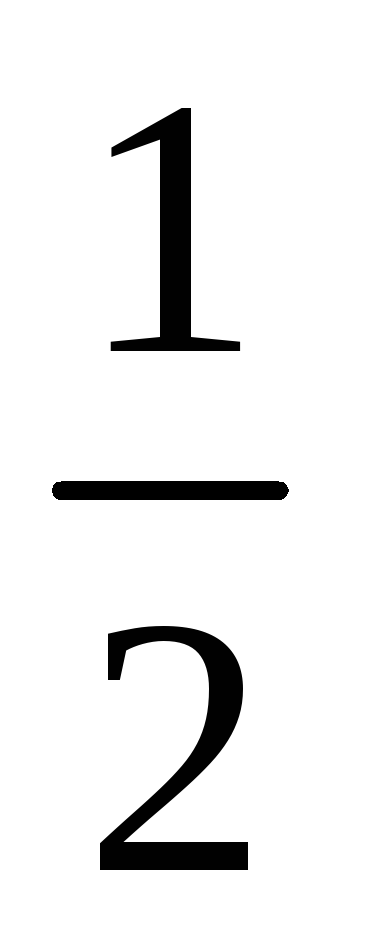
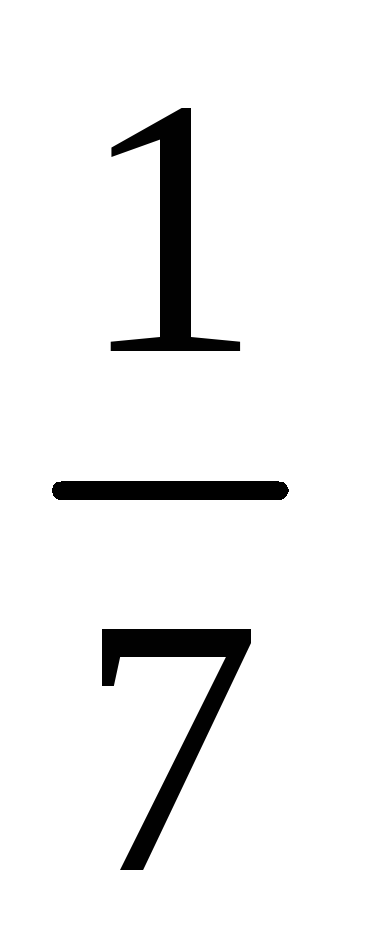
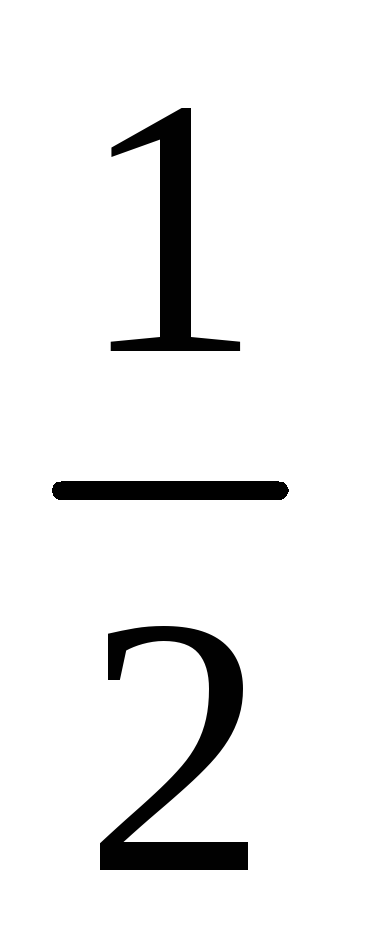
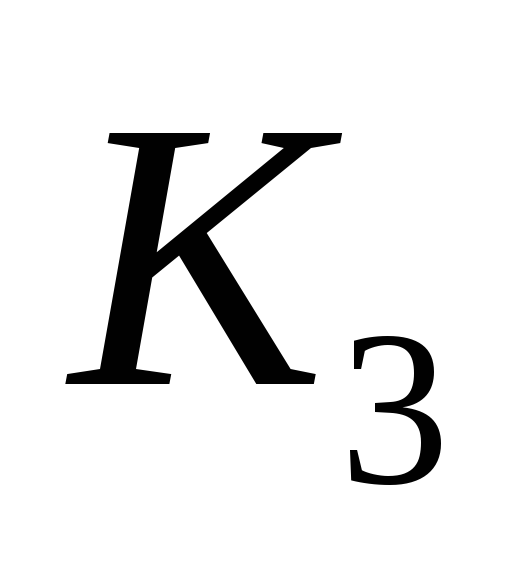
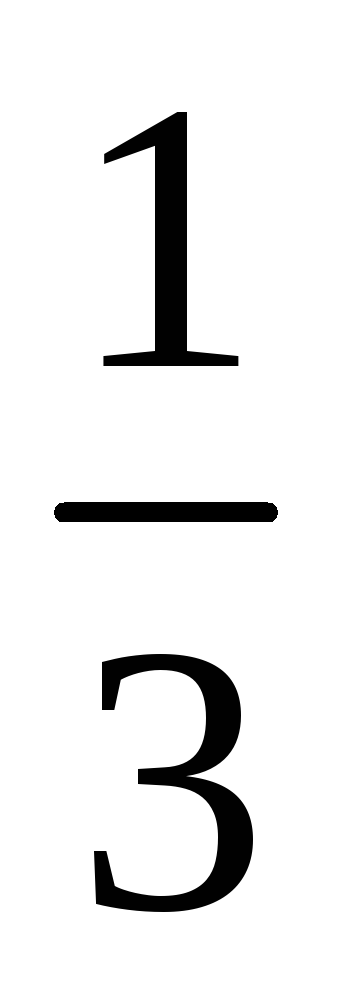
		1	1
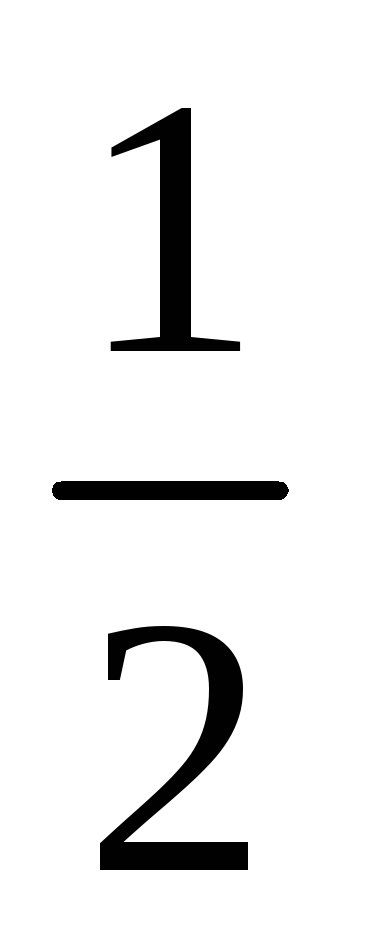
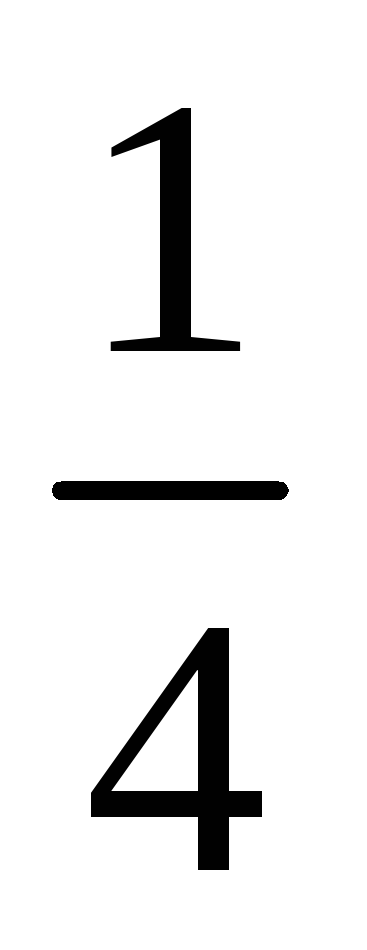
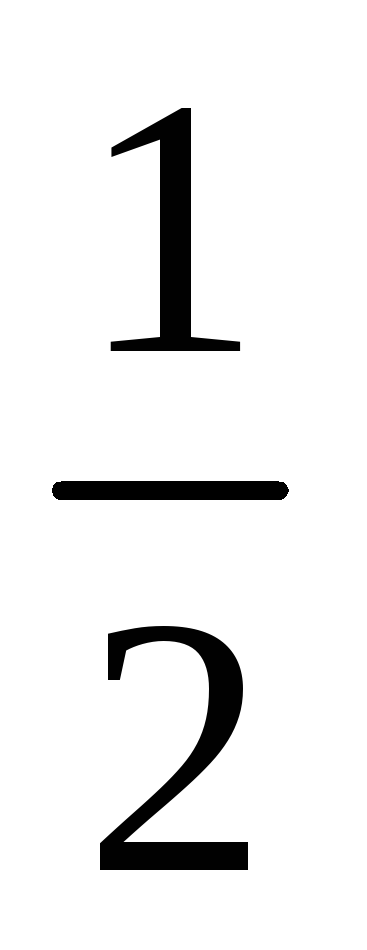
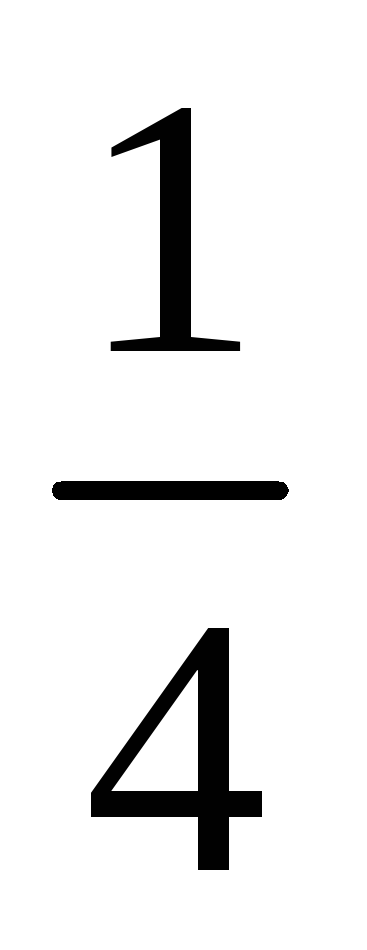
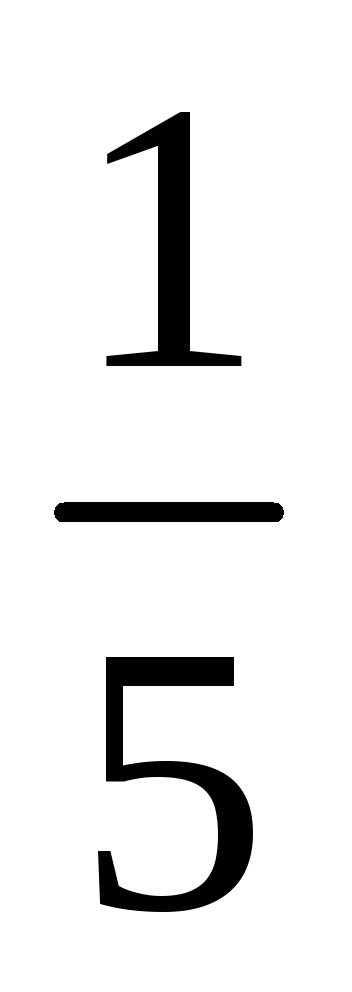
		2	2	1		1
	4	7	4	5	1	3
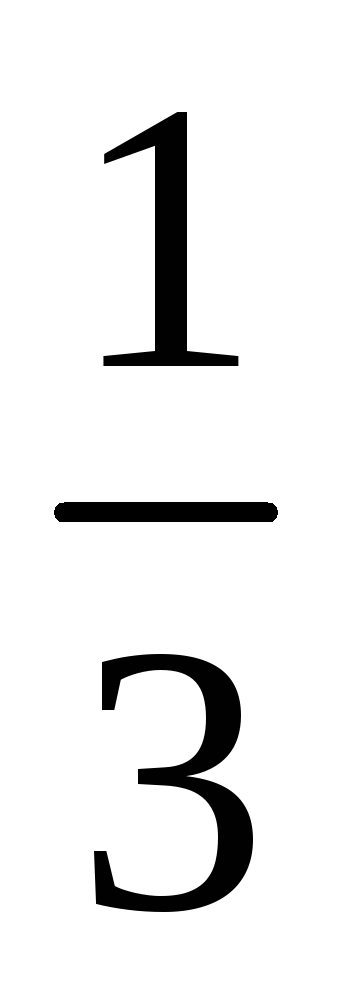
	3	2	2	1		1

Коэффициенты относительной важности критериев и =приведены ниже.

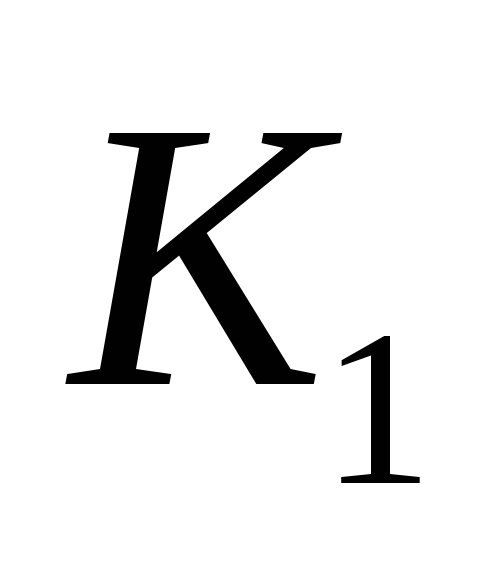
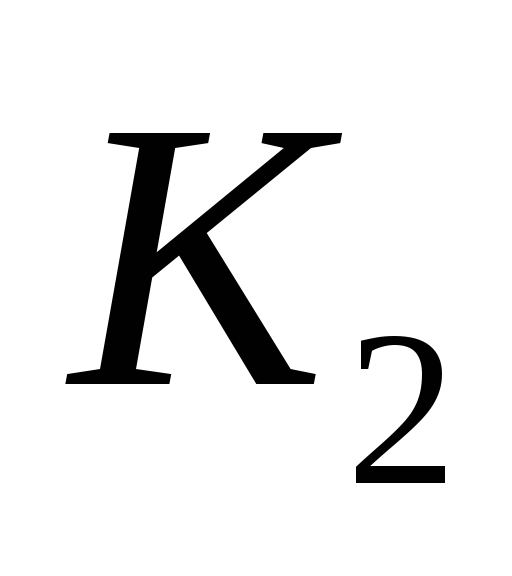
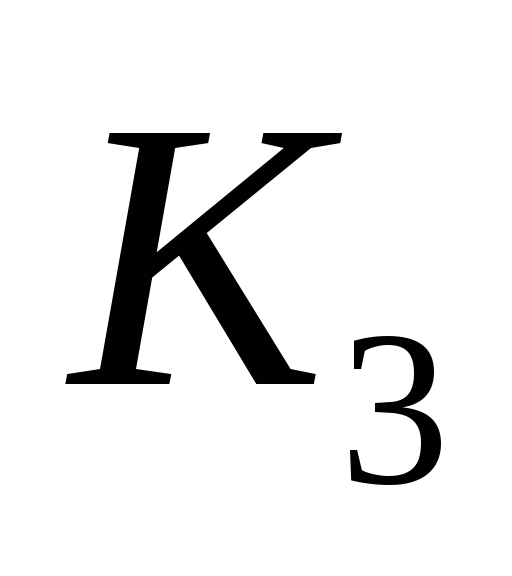
	0,177	0,053	0,067	0,098	0,442	0,162
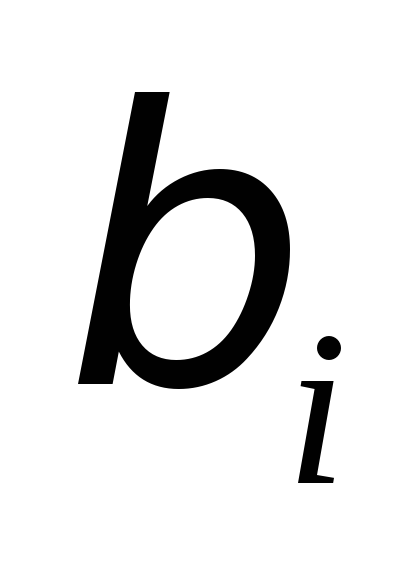
	1,062	0,318	0,404	0,589	2,652	0,972

Множество оптимальных альтернатив с учетом различной важности критериев качества определяется путем пересечения нечетких множеств следующим образом:, а. Найдем множество оптимальных альтернатив с учетом полученных весовых коэффициентов:. Таким образом, лучшей альтернативой является банк, на втором месте банк, самым худшим вариантом для вклада денег является банк.