Тема 4. Принятие решений при нечетком отношении предпочтения на множестве альтернатив §4.1. Нечеткие множества, нечеткие отношения и их свойства

Понятие нечеткого множества – попытка математической формализации нечеткой информации с целью ее использования при построении математических моделей сложных систем. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать данному множеству с различной степенью. При таком подходе высказывания типа «элемент принадлежит данному множеству» теряют смысл, поскольку необходимо указать «насколько сильно» или с какой степенью данный элемент принадлежит данному множеству. Один из простейших способов математического описания нечеткого множества – характеризация степени принадлежности элемента множеству числом, например, из интервала [0, 1]. Пусть - некоторое множество (в обычном смысле) элементов.

Нечетким множеством вназывается совокупность пар, где, а- функция, называемая функцией принадлежности нечеткого множества. Значениеэтой функции для конкретногоназывается степенью принадлежности этого элемента нечеткому множеству. Как видно из этого определения, нечеткое множество вполне описывается своей функцией принадлежности, поэтому ниже мы часто будем использовать эту функцию как обозначение нечеткого множества. Обычные множества составляют подкласс класса нечетких множеств. Таким образом, нечеткое множество представляет собой более широкое понятие, чем обычное множество, в том смысле, что функция принадлежности нечеткого множества может быть, вообще говоря, произвольной функцией.

Нечеткое множество называется пустым, если его функция принадлежности равна нулю на всем множестве , т.е.. Универсальное множествотакже можно описать функцией принадлежности видадля всех.

Объединением нечетких множеств ивназывается нечеткое множествос функцией принадлежности вида.

Пересечением нечетких множеств ивназывается нечеткое множествос функцией принадлежности вида.

Дополнением нечеткого множества вназывается нечеткое множествос функцией принадлежности вида.

Разность нечетких множеств ивопределяется как нечеткое множествос функцией принадлежности вида.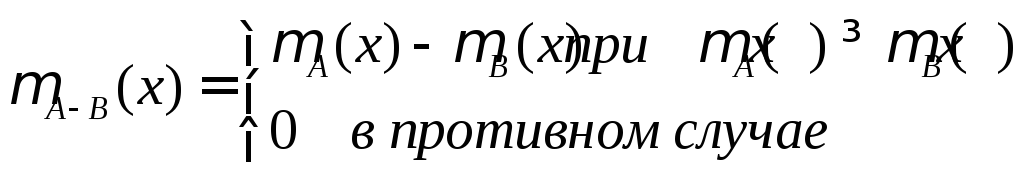

Декартово произведение нечетких множестввопределяется как нечеткое множествов декартовом произведениис функцией принадлежности вида.

Нечетким отношением на множественазывается нечеткое подмножество декартова произведения, характеризующееся функцией принадлежности вида. Значениеэтой функции понимается как субъективная мера или степень выполнения отношения.

Объединением нечетких отношенийивназывается нечеткое отношениес функцией принадлежности вида.

Пересечением нечетких отношений ивназывается нечеткое отношениес функцией принадлежности вида.

Если - нечеткое отношение на множестве, то нечеткое отношение, характеризующееся функцией принадлежностиназывается дополнением вотношения.

Обратное к нечеткое отношениена множествеопределяется функцией принадлежности вида.

Максминное произведение нечетких отношений ивхарактеризуется функцией принадлежности вида.

Рефлексивность. Нечеткое отношение на множественазывается рефлексивным, если для любоговыполняется равенство=1.

Антирефлексивность. Функция принадлежности антирефлексивного нечеткого отношения обладает свойством =0 при любом.

Симметричность. Нечеткое отношение на множественазывается симметричным, если для любыхвыполняется равенство.

Антисимметричность. Функция принадлежности антисимметричного нечеткого отношения обладает следующим свойством: .

Транзитивность. Нечеткое отношение на множественазывается транзитивным, если.

Пример.Пусть универсум есть множество действительных чисел. Нечеткое множество , обозначающее множество чисел, близких к 10, можно задать следующей функцией принадлежности: где.

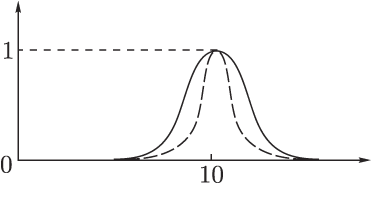
Показатель степени выбирается в зависимости от степени близости к 10. Например, для описания множества чисел, очень близких к 10, можно положить=4; для множества чисел, не очень далеких от 10,=1.

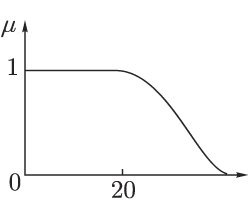
Пример. Остановимся на понятии лингвистической переменной. Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или предложения естественного языка. Например, лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый" и др. Ясно, что переменная "возраст" будет обычной переменной, если ее значения — точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека. Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению "молодой" может соответствовать следующая функция принадлежности.

Пример. Пусть — нечеткое множество "от 5 до 8" и — нечеткое множество "около 4", заданные своими функциями принадлежности:

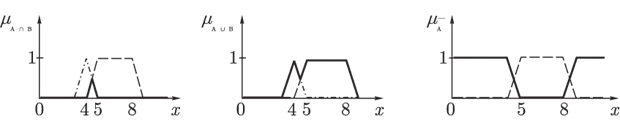
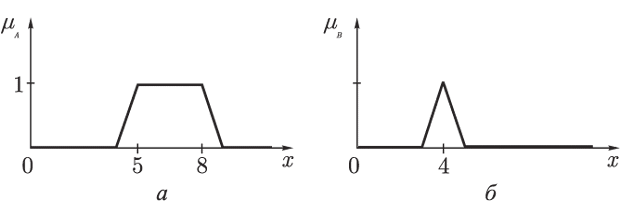Тогда, используя максиминные операции (пересечения, объединения и дополнения), мы получим нечеткие множества, изображенные на следующих рисунках.

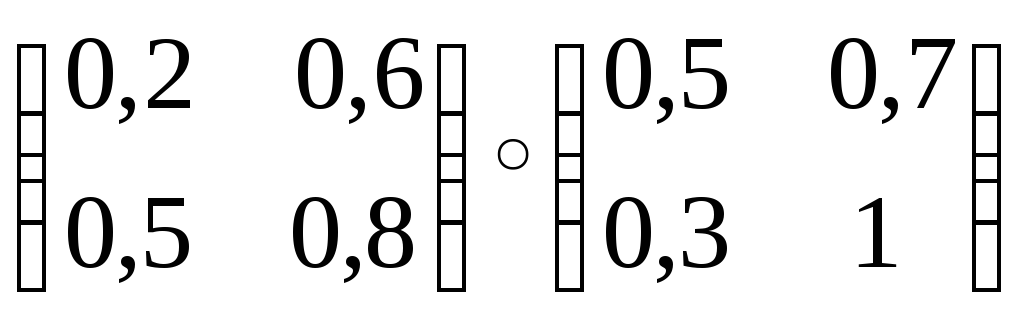
Задание. Найти максминное произведение следующих нечетких отношений:

1.

2.

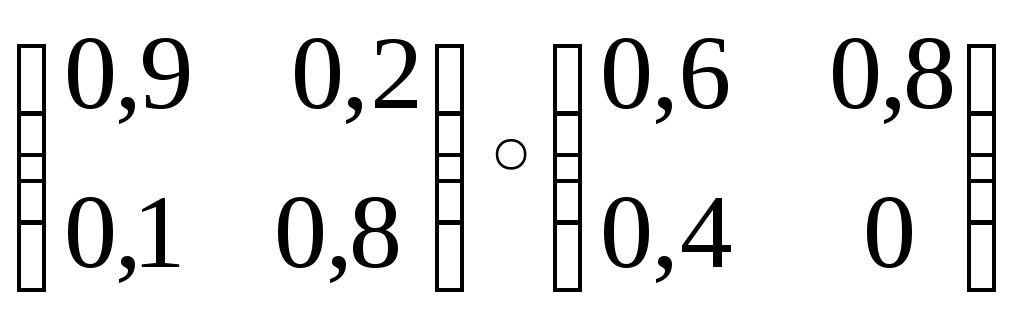
Задание. Проверить на транзитивность следующее нечеткое отношение