
Методы и средства передачи информации (Лекция №17)
.pdf
передачи по каждому из них упадет как минимум втрое и составит примерно 20 км.
Рассмотренный алгоритм оценки параметров радиолинии указывает путь реального процесса расчета линии передачи «прямой видимости». Наличие препятствий между передатчиком и приемником ухудшают уровень передаваемого сигнала на входе приемника и уменьшают длину трассы. Однако учет дифракции электромагнитной волны на препятствии относится к специальным вопросам теории антенн.
Тем не менее, помимо создания радиолиний в свободном пространстве, большое значение представляет задача образования радиолиний в пределах зданий. При этом точные расчеты в таких задачах каждый раз представляют специфический случай, определяемый положением препятствий к распространению волн. Поэтому мы ограничим рассмотрение оценкой затухания волн при их прохождении через плоские стены. Причем рассмотрим алгоритм такой оценки на примере частного случая ортогонального падения плоской электромагнитной волны на слой конечной толщины (модель стены здания) и проникновения волны через этот слой (стену).
3.Применение метода полных сопротивлений и расширенного метода полных сопротивлений для расчета характеристик радиолинии
Поставленная задача расчета проникновения плоской волны внутрь области, ограниченной стенами здания, решается с применением алгоритма, названного методом полных сопротивлений и его развитием – расширенным методом полных сопротивлений. Это рассмотрение ориентировано на оценку радиолиний формируемых, как правило, для создания локальных сетей.
Алгоритм метода полных сопротивлений заключается в сведении задачи распространений электромагнитной волны в проводящей среде к задаче распространения волны в эквивалентной длинной линии. Для обоснования такого подхода рассмотрим сначала задачу поведения плоской волны в однородной среде с потерями, т.е. в можно сказать − проводящей среде.
11

Как мы уже знаем из рассмотрения процессов, определяющих поверхностный эффект, процесс распространения гармонических волн в проводящих средах сопровождается постепенным уменьшением амплитуд векторов напряженностей электрического и магнитного полей, связанных между собой уравнениями поля. В выраженной форме этот эффект наблюдается при распространении волны от поверхности проводника вглубь него (именно поэтому эффект называется поверхностным, или скин, т.е. «кожным» эффектом). В данном случае наш интерес к изучению эффекта в основном связан с вопросами эффективности проникновения электромагнитных волн сквозь стены зданий внутрь помещений (и, наоборот) для создания устойчивых радиолиний.
В нашем случае проводящая среда − среда стены помещения − представляет собой несовершенный диэлектрик, например, или бетон (он имеет εr ≈ 4...5 и tg δ ≈ 0,02...0,03), или кирпич (его εr ≈3 при tg δ ≈ 0,01), а чаще всего − их раз-
личного рода комбинации. Мы ориентируемся на рассмотрение алгоритма оценки распространения волн в средах стен зданий и проникновения волн внутрь помещений, поэтому ограничим наше исследование характеристик сред некоторыми усредненными значениями. Пусть среда распространения волны имеет εr ≈ 4 ,
а её эффективная проводимость
σ = ωε′r′ = ωε′r tg δ ≈ ω 4 0,02 = ω 0,08 См/м.
Для диапазона частот около 1 ГГц (что примерно соответствует типу радиолиний, применяемому для организации радиолиний внутри помещений) эффективная проводимость
σ = ω 0,08 = 2π 109 0,08 ≈5 108 См/м.
Для справки физическая (металлическая) проводимость меди равна 5,7·107 См/м. Тогда в соответствие с известными нам формулами (см. лекцию №12) вторичные параметры, характеризующие радиолинию в такой среде (приняв её от-
носительную магнитную проницаемость равной единице) будут равны
π
p = + jωµ0µrσ = +
jωµ0µrσ = + ωµ0µrσe j 4 = +
ωµ0µrσe j 4 = +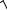 ωµ0µrσe j450 =
ωµ0µrσe j450 =
12
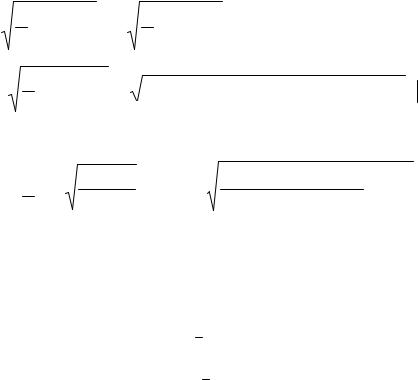
= |
1 ωµ0µrσ + j |
1 ωµ0µrσ = b + jb, |
|
|
|
|
|||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
где b = |
1 ωµ |
0 |
µ |
r |
σ = |
0,5 6,28 4π 10 −7 1 5 10 8 f |
f =1000 МГц |
=1,41·106 |
1/c. |
||
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
а волновое сопротивления |
|
|
|
|
|
||||||
|
Z в = |
|
ωµ0µr e + j450 ≈ |
6,28 10 9 4π 10 −7 |
e + j450 |
≈1,26 10 −3 e+ j450 Ом. |
|||||
|
|
|
|
|
σ |
|
5 108 |
|
|
|
|
С учетом полученных вторичных параметров в такой несовершенной среде можно записать выражения для полей плоской волны, которые в частотной области на расстоянии z от поверхности примут вид:
E = E 0 e − |
pz = E 0 e − αz e − jβz , |
|
|
H = H 0 e − |
pz = H 0 e − αz e − jβz |
(17.7) |
|
при связи между амплитудами напряженностей полей |
E0 и H0 : H0 = E0 / Zв . |
||
Для определения амплитуды поля волны в стене и, соответственно, волны поля прошедшей через стену, надо вспомнить, что поле в стене возникает в результате возбуждения электромагнитных полей на её (стены) поверхности. Эти поля являются результатом «падения» на стену волн источников сигнала. Для определения амплитуды поля в стене надо связать поля падающей на стену волны с полями в стене. Это можно сделать, используя граничные условия (ГУ).
Для упрощения анализа приближенно примем волны, падающие на стену, за плоские волны. Конечно, такое допущение справедливо лишь при расстояниях от источника излучения много бόльших длины волны, и не столько в плане рассмотрения волны в зоне излучения, а исходя из возможности пренебрежения кривизной синфазной поверхности фронта сферической волны в сравнении с размерами объекта. Строго говоря, такое допущение на практике не справедливо для волн с частотой 1 ГГц, у которых длина волны составляет всего 0,3 м, для которых зона излучения, равная примерно (6…7)λ, хотя и составляет 2…3 м, а область, в которой волну можно считать плоской в сравнении с размерами стены помещений (не говоря о размерах стен зданий) требует удаления источника на
13

существенно бόльшие расстояния, которые не соответствуют практическим расстояниям радиолиний в таких локальных сетях.
Темнее менее, строгое решение задачи (т.е. при рассмотрении процессов распространения в стене сферических волн) на практике не имеет рационального действия, так как не поддерживается в расчетной модели достоверной сложной неоднородной системой (системой слоев), соответствующей реальной среде.
Итак, полагаем вектор Пойнтинга направленным ортогонально поверхности плоской (бесконечной во все стороны) стены и согласно общему решению уравнений Максвелла в свободном пространстве представим структуру полей волны в полупространстве до стены (внешнем, обозначенном индексом «вш») уравнениями
E |
вшτ |
= Z |
H |
0 |
(A e− jk0 z + A e jk0 z); |
(17.8) |
|||
|
0 |
|
|
1 |
2 |
|
|||
Н |
вшτ |
= H |
0 |
(A e− jk0 z |
+ A e jk0 z), |
(17.9) |
|||
|
|
|
|
|
1 |
2 |
|
||
где индекс τ − тангенциальная (касательная) к поверхности экрана компонента
поля; Z0 = |
µ0 − волновое сопротивление |
Zв свободного пространства; H0 − |
|
ε0 |
|
амплитуда поля в свободном пространстве; |
εr =µr =1(пространство − воздух); |
|
k0 = ω ε0µ0 ; A1, А2 – постоянные интегрирования − амплитуда прямой и обрат-
ной волн, определяемые из ГУ на поверхности экрана.
Здесь отсчетная плоскость (начало оси z) пока не определена. В дальнейшем примем за начало отсчета оси z плоскость стены, на которую падает волна излучателя.
АмплитудуH0 поля в свободном пространстве приближенно оценим, исхо-
дя из мощности излучателя P, предполагая его, например, вибратором с длиной l<λ. Тогда согласно лекции № 15 амплитуда напряженности магнитного поля на расстоянии r от источника приближенно равна
H0 ≈ |
I l |
= |
Pl |
|
= |
Pl λ2 |
≈ |
P |
А/м, |
(17.10) |
|
2λr |
|
2λr RΣ |
εr =1 |
2λr 80π2l2 |
|
18 πr |
|
|
|
|
|
|
|
µr |
=1 |
|
|
|
|
|
|
|
|
|
Z0 |
=120π |
|
|
|
|
|
14

где |
RΣ =80π |
2 |
l |
2 |
|
− сопротивление излучения вибраторной антенны в |
||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
λ |
|
εr =1 |
||
|
|
|
|
|
|
|
µr |
=1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Z0 |
=120π |
воздушном пространстве, размерность Ом.
Постоянные интегрирования можно определить, применяя ГУ в виде приравнивания тангенциальных составляющих напряженностей полей и нормальных составляющих магнитной и электрической их индукций. Этот путь более трудоёмкий, чем алгоритм определения постоянных интегрирования на основе рассмотрения волновых процессов в радиолинии в терминах длинной линии.
Применим ГУ на поверхности стены в приближении скачкообразного изменения волнового сопротивления в длинной линии − модели радиолинии (при переходе из окружающего пространства в среду стенки экрана). Выражения для волн в стене (17.7) во временной области повторяют формулы (17.8) и (17.9), но
при замене |
jk0 на постоянную распространения p = jωµ0µrσ и при Z в = Z ст =. |
|
= |
jωµ0µr |
. Таким образом, стационарное распределение полей во внешнем |
|
σ |
|
пространстве непосредственно вблизи плоскости стены для гармонических сигналов в частотной области, определится коэффициентом отражения волны излучателя в сечении стены
|
|
|
|
|
|
|
|
|
|
n |
0 |
= |
Zн − Z0 |
, |
|
(17.11) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Zн + Z0 |
|
|
|
||||
где |
Z н = Z э |
Z |
′н + Z′ст th pd |
, |
|
|
|
|
|
|
|
|
|
(17.12) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Z |
′н th pd + Z′ст |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z′н = Z0 = |
|
µ0 |
− волновое сопротивление пространства за стеной – «сво- |
||||||||||||||||
|
|
ε0 |
||||||||||||||||||
бодное» пространство ( σ = 0 ; µr =1; εr =1); |
|
|
||||||||||||||||||
|
d– толщина стены в направлении оси z перпендикулярной её плоскости. |
|||||||||||||||||||
|
Откуда E |
вш отр |
= n E |
вш |
= |
|
Zн |
− Z0 |
E |
вш |
, |
(17.13) |
||||||||
|
|
Zн |
|
|||||||||||||||||
|
|
|
|
0 |
|
|
|
+ Z0 |
|
|
||||||||||
15
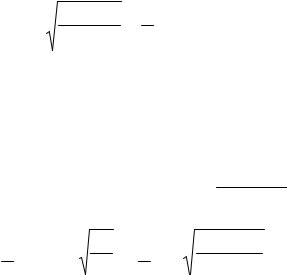
H |
вш отр |
= −n H |
вш |
= |
Zн − Z0 |
H |
вш |
. |
(17.14) |
|
|||||||||
|
0 |
|
Zн + Z0 |
|
|
||||
Внутри стены непосредственно на границе, из ГУ на границе раздела полу- |
|||||||||
чается: |
|
|
|
|
|
|
|
|
|
E |
прош |
= E |
вш |
+ E |
вшотр |
= |
2 Zн |
E |
вш |
; |
(17.15) |
|
|||||||||||
|
|
|
|
Zн + Z0 |
|
|
|||||
Н |
прош |
= Н |
вш |
+ Н |
вшотр |
= |
2 Z0 |
Н |
вш |
. |
(17.16) |
|
|||||||||||
|
|
|
|
Zн + Z0 |
|
|
|||||
В действительности поля внутри стены нас не интересуют. Нас интересует |
|||||||||||
поле в помещении за стеной в «ограничиваемом» ею полупространстве. Это поле определится волной, дошедшей до стены, ограничивающей внутреннюю полу-
плоскость (в техническом смысле − помещение). Эта волна определяется коэф-
фициентом затухания. Обозначив волны в стене Ecт , Нст, а индексами 1 и 2 – по-
верхности стенки, соприкасающиеся с внешним (вш) и внутренним (вт) пространствами, можно (следуя традиционному подходу) записать:
|
|
− |
d |
|
|
|
||
|
|
|
|
|
||||
|
Eст2 = Eпрош е−αz = Eпрош е |
|
δ , |
(17.17) |
||||
|
Нст2 = Нпрош е−αz = Нпрош е |
− |
d |
|
|
|||
|
δ , |
(17.18) |
||||||
|
|
|
||||||
где ось z отсчитывается внутрь стенки от её поверхности; |
|
|||||||
δ = |
2 |
= 1 − глубина проникновения, обратно |
пропорциональная |
|||||
|
ωµ0µrσ |
α |
|
|
|
|
|
|
коэффициенту затухания (по дефиниции термина).
Волна, прошедшая в область за стеной, может быть получена с использованием коэффициента отражения в сечении 2 стены:
n 02 = Z 0 −Z ст , (17.19)
Z 0 + Z ст
где Z0 = Z0 = |
µ0 ; Z ст = |
jωµ0 µr |
, |
|
ε0 |
σ |
|
с помощью которого определяются отраженные волны в стене:
16

~ |
|
Z 0 |
|
|
2 Z н |
|
− |
d |
|
|
|
δ |
|
|
|||||||
|
−Z ст |
|
|
Eвш |
|
|||||
Eстотр = п02 Eст2 |
= |
|
|
|
|
e |
|
|
, |
|
|
|
|
|
|
||||||
|
Z 0 |
+ Z ст Z н + Z 0 |
|
|
|
|
|
|||
Hстотр = −п~02 H ст2 = Z ст −Z 0 2 Z 0 e−dδ H вш
Z 0 + Z ст Z н + Z 0
иволны в помещении за стеной (но непосредственно на стене) в виде:
|
|
|
|
|
|
|
4 Z 0 Z н |
|
|
|
− |
d |
|
|
|
|
|||
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|||||||
Eвт2 = Eст2 + Eстотр = |
|
|
|
|
|
Eвш; |
|
||||||||||||
|
|
|
|
|
e |
|
|
|
|||||||||||
(Z 0 |
+ Z ст )(Z н + Z 0 ) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
4 Z 0 Z ст |
|
|
|
|
|
− |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
H |
|
= H |
|
− H |
|
= |
|
|
|
|
|
e |
|
δ H |
|
. |
|||
|
|
|
|
0 + Z ст )(Z н + Z |
|
|
|
|
|
||||||||||
|
вт2 |
|
ст2 |
|
стотр |
|
(Z |
0 ) |
|
|
|
|
вш |
|
|||||
(17.20)
(17.21)
(17.22)
(17.23)
Заметим, однако, что выражение (17.19) и вытекающие из него (17.20)…(17.23) получены в предположении бесконечной длины «трассы» во внутренней полости (т.е. Zвх на границе стены со стороны комнаты равна Z0 ).
На рис. 17.1 представлена схематическая конструкция «трасы» и ее эквивалентная схема замещения в терминах электрической схемы с распределенными
|
|
|
Евш |
|
I |
|
1 |
|
II |
2 |
|
III |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Епрош |
|
|
Евт |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Пвш |
|
|
Ппрош |
|
|
|
|
|||||
Нвш |
|
0 |
|
|
d |
Пвт z |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Нпрош |
|
|
Нвт |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ = 0; εr =1; µr =1 |
σ ≠ 0; εr =1; µr ≠1 |
|
σ = 0; εr =1; µr =1 |
||||||||||||||
vф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vф |
|
|
|
|
Z0 |
|
v ≈ |
|
|
C ; Z = Z |
|
|
|
vф = ω/ β; Zв ≠ Z0 |
|
|
vф ≈C0 ; Zв = Z0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
ф |
|
0 |
в |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z вx= Zн |
Zвx = Z0 |
|
|
||||||||
Рисунок 17.1 − Схематическая конструкция стены помещения − а и ее ценное представление −б: I, II и III – области окружающего пространства и области за стеной (комнаты); 1, 2 – границы стены
параметрами. Выражения (17.20) и (17.21) не учитывают также переотражений волн внутри экрана. Ограничимся на первом этапе приближением бесконечности экранируемой области и запишем более строгое выражение для Eвт2 и Hвт2 ,
17

используя гиперболические уравнения для длинных линий (т.е. уравнения с ис-
пользованием [А] − матрицы). Это решение учтет переотражения внутри стенки экрана.
В соответствии с уравнениями длинных линий, заменив U на E и I на H ,
для длинной линии (ДЛ) области 2 можно записать:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eпрош = H вт{Z0 ch pd + Zст sh pd } |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
(17.24) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Z0 |
sh pd +ch pd |
|
||||||||||||||||||||
|
|
Н |
прош |
= H |
вт |
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
Zст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где H вт = Eвт |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С учетом (17.15), (17.16) и Eвш = Z0Нвшзапишем (17.24) в виде |
|
||||||||||||||||||||||||||||||
|
|
|
2 Z н |
|
Eвш |
= Eвт |
|
1 |
{Z0 ch pd + Z ст sh pd} |
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Z |
н + Z 0 |
|
|
|
|
|
|
|
Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(17.25) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
E |
вш |
= E |
вт |
|
|
Z0 |
sh pd +ch pd |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Z |
н + Z 0 |
|
|
|
|
|
|
|
Z0 Z ст |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из второго уравнения системы (17.25) после несложных преобразований с учетом (17.12) получим:
Eвт = |
|
|
|
|
|
|
2Z0 |
|
|
|
|
|
Eвш . |
(17.26) |
|
|
|
|
|
Z0 |
|
|
|
|
Z0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
chрd Zст |
|
+ th pd |
+ Z0 |
|
th pd +1 |
|
|
|||||||
|
|
|
|
Zст |
|
|
|
Zст |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
Заметим, что аналогичный результат можно получить и с использованием волновых матриц.
Примененный алгоритм расчета полей в ограниченном полупространстве называется «метод полных сопротивлений». Основное назначение алгоритма − расчет (точнее − оценка) экранирующих свойств различных полостей, образованных параллельными стенками. Причем расчет поля в ограниченной области с применением этого метода не учитывает влияния противоположной стенки по-
18

лости, а в нашем применении этого алгоритма (для расчета радиолинии с препятствием в виде стены помещения) не учитывает влияния противоположной стены на уровень поля внутри помещения.
Учесть влияние обеих параллельных стенок области (а в нашем случае − стенок помещения) на уровень поля, проникающего в неё, можно с применением расширенного метода полных сопротивлений. По существу этот алгоритм повторяет действия «метода полных сопротивлений», но «продлевает» трассу (радиолинию) до области за второй стенкой.
Основное применение расширенного метода полных сопротивлений − расчет (оценка) экранирующего действия металлических полостей, т.е. замкнутых экранов. Этот метод (также как и предыдущий) пригоден лишь для приближенных оценок, так как:
1)при расчете учитывается лишь действие параллельных плоских стенок и не учитывается влияние ортогональных им стенок, замыкающих исследуемую область;
2)метод не позволяет учитывать влияние неоднородностей в стенах, или неоднородностей в стенках экранов (отверстий вводов питания, сигнальных цепей, вентиляционных отверстий, отверстий для ручек управления и пр.) и неоднородных граничных условий во внутренней полости, в том числе, и ребер за счет пересечения ортогональных стенок и особенно − углов − точек пересечения ребер;
3)метод справедлив лишь при нормальном падении плоской волны (помехи) на плоскость стенки экрана, т.е. в строгой постановке задачи он не пригоден для оценок свойств радиолиний (или свойств экранов) в полях зоны индукции.
Рассмотрим алгоритм и результаты применения метода для плоскопараллельной системы бесконечных стен, изображенной на рис. 17.2 при нормальном падении плоской волны. При этом известным будем считать амплитуды полей
плоской волны (Нвш и Евш = Zo Нвш ).
Цель расчета – определение амплитуд полей Нвт и Евт в области между сте-
нами в точке М (в центре комнаты рис. 17.2).
19

Расчет можно осуществить в приближении [A]– матриц (в гиперболических
функциях) аналогично предыдущем случаю (где полагалось расстояние между стенами a = ∞), или на основе [S] – матриц рассеяния (см. лекцию № 13), но
удобнее всего применить метод волновых [T]– матриц передачи, которые для линейного ЧП, образованного системой рис. 17.2, вводятся уравнением
Rвх |
T11 |
T12 |
|
Rвых |
(17.27) |
||
|
|
= |
|
|
= |
, |
|
Lвх |
T21 |
T22 |
Lвых |
|
|||
где R и L– прямые и обратные волны на входе и выходе ЧП.
Такое описание ЧП позволяет (см. лекцию № 13) для каскадного соединения
n ЧП записать волновую матрицу передачи [T]в виде произведения волновых матриц передачи [Ti]входящих в нее ЧП:
|
|
|
[T]=[T1] [T2] [T3]...[Tn]. |
|
(17.28) |
||||||||||
I |
|
|
|
II |
|
|
|
III |
|
IV |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Z0; k0 |
|
Zст; |
|
Z0; k0 |
|
|
|
Zст; |
|
Z0; k0 |
|||||
П |
|
kст |
|
|
|
|
|
|
kст |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
Rвх = a1 |
~ |
|
|
|
|
|
|
|
|
Rвых = a1 |
|||||
|
|
|
|
|
|
|
|||||||||
|
a1 |
|
a1 |
|
|
|
|
|
|||||||
Lвх = b1 |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
||
|
a2 |
|
|
|
|
|
|
|
Lвых = b1 |
||||||
|
|
a2 |
|
|
|
|
|
||||||||
|
|
|
~ |
|
|
|
~ |
|
M |
|
|
z |
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
b1 |
|
b1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
а/2 |
3 |
4 |
|
|
|
|
|
|
|
d |
а |
|
d |
|
Рисунок 17.2 − Структуры границ образованных плоскими стенками: области 1 и 3 − проводящие стенки толщиной d; 0 , 2 , 4 – области без потерь; ai - падающие волны; bi - отраженные волны; R – прямые (вдоль оси z0 ) и L – обратные (против оси z0 ) волны. Римские цифры – границы областей
20
