
Методы и средства передачи информации (Лекция №15)
.pdf
Методы и средства передачи
 информации
информации
Лекционный курс
Лекция № 15
Содержание
1.Распространение электромагнитных волн в свободном пространстве
2.Волновые уравнения и их решения. Запаздывающие потенциалы
3.Поле диполя Герца
4.Поле плоского кругового витка с током
1.Распространение электромагнитных волн в свободном пространстве
До этой лекции наше внимание было сосредоточено на рассмотрении различных аспектов построения каналов передачи информационных сообщений с применением конструктивно оформленных линий передачи. Это оправдано тем, что до последнего времени именно такие структуры представляли основу методов и средств передачи цифровой информации. Тем не менее, с ростом объёма информационных потоков и расширением информационных сетей все большее значение приобретают радиоканальные варианты формирования информационных потоков. В плане бытовых названий эти структуры могут называться (и в быту называются) различными звучными идентификаторами, например, Wi-Fi (Wireless Fidelity – дословно – «беспроводная достоверность») или Blue Tooths («голубые зубы» – идеоматическое выражение (фразеологизм — оборот речи, употребляющийся как единое целое), которое имеет устоявшееся имя– «последняя миля» и обозначает беспроводную связь). Основное преимущество радио каналов отсутствие конструктивных линий, а значит оперативность образования и меньшая стоимость.
Основа радиоканалов – передача информационных сигналов за счет распространения радиоволн в свободном пространстве. Это обеспечивается за счет создания элементов связи между источниками сигнала и пространством распространения волны, а также обратным преобразованием «пришедших» радиоволн (т.е. пришедших к местоположению приемного устройства электромагнитных
волн информационного сигнала) в электрические сигнала (токи и напряжения) на входе приемного устройства. Эти элементы связи называются антенными устройствами, или просто антеннами. Эти элементы связи, как правило, линейные электрические цепи и в соответствии с принципом взаимности линейных цепей с одинаковым успехом могут служить как источниками, так и приемниками электромагнитных волн.
Антенны – конструктивно достаточно простые устройства, однако простота конструкции скрывает очень сложные математические алгоритмы рационального проектирования геометрических размеров таких устройств, согласованных с окружающим пространством в различных частотных диапазонах и при особенностях требуемых радиотрасс.
Для понимания и оценки применимости различных антенн к различным условиям их эксплуатации, необходимо обладать хотя бы минимальными знаниями относительно физических особенностей распространения электромагнитных волн в окружающем пространстве и свойств излучателей (приемников) такиэ волн.
2.Волновые уравнения и их решения. Запаздывающие потенциалы
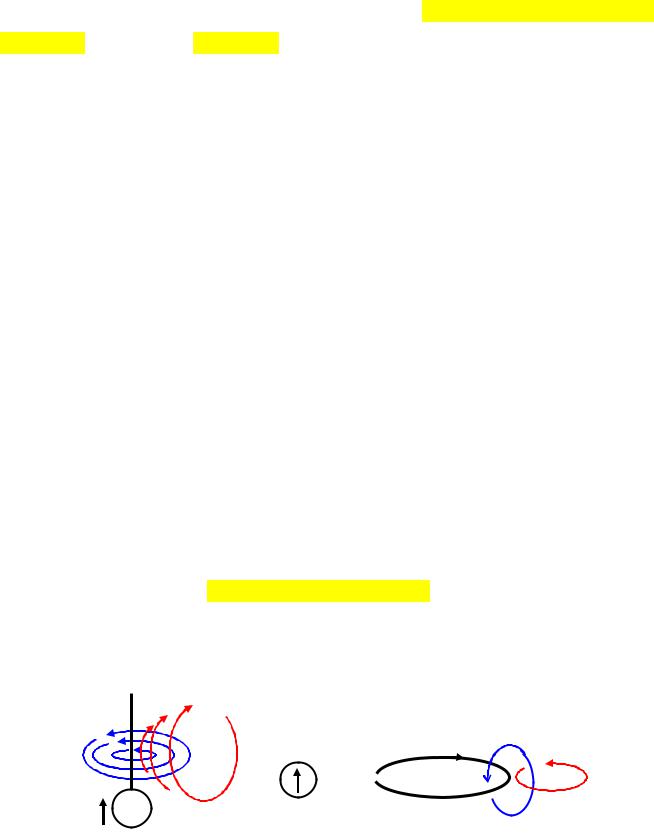
Изучение излучающих структур традиционно основывается на предварительном анализе свойств элементарных излучателей, которые называют диполями. К ним относят электрический (Герца) и магнитный (Фитцжеральда), соответственно, электрический вибратор и рамка с током, показанные на рис. 15.1.
H |
|
|
E |
H |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i(t) |
~ |
u(t) |
|
|
|
i(t) |
E |
|
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
||
Рисунок 15.1– Элементарные излучатели: вибратор (а); рамка с током (б)
2

Модель вибратора определяется электрическим моментом p = i l , где i – ток в диполе (вибраторе), определяемый dq / dt , l – длина вибратора (рис. 15.2,
а).
|
|
p(t) = i(t) l |
pм(t) = i(t) S = i(t) 2πR |
||
|
|
|
|
-q |
i(t) |
|
|
|
|
||
l |
|
|
|
i(t) |
|
|
|
|
R – радиус рамки |
||
|
|
|
|
+q |
б) |
|
|
|
|||
|
|
а) |
|||
Рисунок 15.2 – Модели диполей: а - электрического; б – магнитного
Модель рамки вводится магнитным моментом pм= i S , где i – ток, а S –
площадь рамки (рис. 3.2, б). Ещё раз напомним, что слово «диполь» характеризует малые размеры излучателя (а не то, что он – двухполюсник).
Интерес к элементарным излучателям объясняется тем, что более сложные структуры в ряде случаев с применением принципа суперпозиции удается свести к наложению полей элементарных излучателей. Кроме того, понятия, вводимые для анализа простейших излучателей, успешно применятся к характеристике свойств более сложных структур.
Расчет полей, возбуждаемых элементарными излучателями в свободном пространстве (т.е., при отсутствии иных граничных условий, кроме условий на излучателе и на бесконечности), реализуется интегрированием системы уравнений Максвелла.
Уравнения Максвелла для однородной среды имеют вид:
rot H = j + ε0 |
εr |
∂E |
, |
|
||||
∂t |
|
|||||||
|
|
|
|
|
|
|||
rot E = −µ0µr |
∂H |
|
, |
(15.1) |
||||
∂t |
||||||||
|
|
|
|
|
||||
div E = |
ρ |
, |
|
|
|
|
|
|
ε0εr |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
divµ0µr H = 0 .
3

где εr и µr – относительные диэлектрическая и магнитная проницаемости про-
странства, возникающие в, так называемых, «материальных» уравнениях:
D =ε0εr E и B =µ0µr H.
Для краткости дальнейших записей введем обозначения:
ε0εr = ε, µ0µr = µ.
Используя введенные ранее обозначения оператора Набла –
= x |
o |
∂ |
+ y |
o ∂ |
+ z |
o ∂ |
||
|
∂x |
|
∂y |
|
∂z |
|||
|
|
|
|
|
|
|||
и применив второй вариант решения уравнений Максвелла – замена переменных E и H на вспомогательные функции – потенциалы: скалярный ϕ и векторный
A, который дополняем калибровкой Лоренца, получаем уравнение для векторного и скалярного потенциалов в виде:
2 A − εµ ∂2 A = −µj ,
∂t 2
2 |
ϕ − εµ |
∂2 |
ϕ |
= − |
ρ |
. |
(15.2) |
|
∂t |
2 |
ε |
||||||
|
|
|
|
|
Из выражений (15.1) и (15.2) видно, что и скалярная функция ϕ(x,y,z,t), и
проекции векторной функции A(x, y, z,t) на координатные оси x0 ,y0 ,z0 удовле-
творяют уравнению одного и того же типа – уравнению Даламбера
2 Φ−εµ∂ 2 Φ |
=−η . |
(15.3) |
||
∂t 2 |
|
|
|
|
Решение уравнения (15.3) – функции бегущей волны, покажем это. |
||||
Наиболее просто это можно показать для волнового уравнения |
|
|||
2Φ − εµ |
∂2Φ |
= 0, |
(15.4) |
|
∂t 2 |
|
|||
|
|
|
|
|
которое является частным случаем уравнения Даламбера для области анализа полей, свободной от сторонних источников, чему соответствует равенство нулю
4
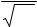
правой части уравнения (15.3), то есть η= 0 , в декартовой системе координат
при условии, что Ф( x, y, z, t)= Ф(z, t). |
|
|
|
|
|
|||||||||
При этом 2 |
Φ = |
∂2 |
Φ |
и уравнение (15.4) принимает вид одномерного од- |
||||||||||
∂z2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
нородного уравнения в частных производных |
|
|
|
|||||||||||
|
|
∂2Φ |
− εµ |
∂2Φ |
= 0, |
|
|
|
|
|||||
|
|
∂z2 |
∂t 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
решение которого имеет вид |
|
z |
|
|
|
z |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Φ = Φ1 t |
− |
|
|
|
+ Φ2 |
t + |
|
, |
(15.5) |
|||
|
|
v |
|
|||||||||||
|
|
|
|
|
|
|
|
|
v |
|
||||
где Φ1 и Φ2 − функции бегущих плоских (т. е., с плоским фронтом) волн, у кото-
рых v = |
1 |
– фазовая скорость. Причем волна Φ1 распространяется c фазовой |
|
εµ |
|
скоростью v вдоль оси z, а Φ2 − в обратном направлении.
В сферической системе координат для полей точечного источника (в про-
странстве вне источника) волновое уравнение имеет вид: |
|
||||||||
∂2Φ |
+ |
2 |
∂Φ |
− εµ |
∂2 |
Φ |
= 0 , |
(15.6) |
|
∂r 2 |
r |
∂r |
∂t 2 |
||||||
|
|
|
|
||||||
14243 |
|
|
|
|
|
||||
2 Φ
аего решение получается с применением подстановки ζ = Φ r , приведением
(15.6) к виду
∂2ζ |
− εµ |
∂2ζ |
= 0 |
|
∂r 2 |
∂t 2 |
|||
|
|
и новая переменная ζ аналогично (15.5) записывается как
ζ = ζ1 |
|
r |
+ ζ2 |
|
r |
t − |
|
t + |
. |
||
|
|
v |
|
|
v |
Откуда с обратной заменой переменных получим решение уравнения (15.6)
|
|
|
|
r |
|
|
|
r |
||||
|
Φ1 |
t |
− |
|
|
Φ2 |
t |
+ |
|
|
||
|
|
|||||||||||
Φ = |
|
|
|
v |
+ |
|
|
|
v |
, |
||
|
r |
|
|
|
r |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
5

где Φr1 и Φr2 – сферические волны (соответственно, прямая и обратная, или
отраженная ).
Вид функции Φ1 определяется источником, а обратной функции Φ2 –
причиной отражения.
Для точечного источника вид функции Φ1 можно установить, рассматри-
вая решение задачи для точечного электрического заряда в точке r= 0. Уравнение Даламбера для ϕ( t ) при постоянном заряде q (то есть, при
∂∂t →0 ) переходит в «электростатическое уравнение» Пуассона для потенциала
ϕ(r ), решение которого для точечного заряда имеет вид
ϕ(r) = |
q |
. |
(15.7) |
|
4πεr |
||||
|
|
|
||
Полагая q = q(t), но при фазовой скорости волн v |
→∞, что соответствует |
|||
очень медленным процессам во времени, можно выражение (15.7) распростра-
нить на случай ϕ(t) и записать решение в виде
ϕ(r,t) = |
|
q(t) |
. |
|
|
(15.8) |
|
|
4πεr |
|
|||||
|
|
|
|
|
|
|
|
Теперь, зная, что решение волнового уравнения выражается в функции бе- |
|||||||
гущих волн, если предположить, что при фазовой скорости v ≠ ∞, |
|
||||||
|
|
|
|
r |
|
|
|
|
q t − |
|
|
|
|
|
|
|
|
|
|
|
|||
ϕ(r,t) = |
|
|
|
v |
, |
(15.9) |
|
|
4πεr |
||||||
|
|
|
|
||||
то при v →∞, выражение (15.9) перейдет в (15.8), то есть решение (15.9) явля-
ется предельным переходом для более общего решения (15.9).
Заметим, что мы лишь показали, какой вид функции логично ожидать.
Из решения задачи для точечного источника следует решение для потенциала в точке наблюдения М от распределенного в объеме V заряда
ρ(x, y, z, t).
6

ϕ = |
1 |
V∫ |
ρ(t − r v) |
dV . |
(15.10) |
4πε0ε′ |
r |
Важно отметить, что в точке наблюдения M в момент времени t суммиру-
 М
М
ρ1 r'
r"
 ρ2
ρ2
Рисунок 15.3. Суммирование в точке М потенциалов от двух зарядов
ются парциальные потенциалы ϕk от значений ρk(t,r), взятых в разные моменты
времени t'= t – r'/v, что иллюстрирует рис. 15.3.
Этот факт и характеризует понятие «запаздывающие потенциалы». Аналогично, рассмотрев выражение для векторного потенциала A элемен-
та постоянного тока Il (закон Био-Савара) и формально перейдя от уравнения Пуассона к уравнению Даламбера, можно записать для векторного потенциала A(r,t) выражение
A(r,t)= |
µ |
∫ |
j(t − r v) |
dV . |
(15.11) |
4π |
r |
V
Поэтому, в отличие от скалярного ϕ и векторного A потенциалов элек-
тростатического и стационарного полей, потенциалы электромагнитного поля называют «запаздывающими» – т. е. учитывающими время распространения волны.
Для линейных зарядов τ(r,t) и токов i(r,t) формулы |
(15.10) и (15.11) |
|||||||||
принимают вид: |
|
|
|
|
|
|
|
|
||
ϕ = |
1 |
∫ |
|
τ(t − r v) |
dl , |
(15.12) |
||||
4πε |
|
|
||||||||
|
l |
|
|
r |
|
|||||
|
|
|
|
|
|
|
|
|
||
A = |
µ |
∫ |
i(t − r v) |
dl . |
(15.13) |
|||||
4π |
r |
|||||||||
|
|
|
|
|
l |
|
||||
7
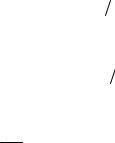
Нагляднее запаздывание по времени проявляется при рассмотрении гармонических процессов.
Здесь, переходя в частотную область, т. е., представляя временные функции в виде разложения в комплексные ряды Фурье (для гармонических процессов – один член разложения):
|
|
|
|
|
|
|
ωr |
|
|
|
|
|
|
|
|
|
jω t−r |
v |
|
− j |
|
|
jωt |
|
− jkr |
|
jωt |
|
|
|
|
|
|
|
|
|||||||||
|
|
=Ie |
|
v e |
=Ie |
e |
, |
|||||||
i t ↔Ie |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jω( t−r |
v ) |
=τe |
− jkr |
e |
jωt |
, |
|
|
|
|
||
τ t ↔τe |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(здесь k = ωv = 2λπ ), можно записать:
ϕ= |
|
1 |
∫ |
τ e −ikr |
dl , |
|
4 |
πε |
r |
||||
|
l |
|
||||
|
|
|
|
|
(15.14)
(15.15)
(15.16)
A = |
µ |
∫ |
I e−ikr |
dl . |
(15.17) |
4π |
r |
||||
|
|
l |
|
|
|
Напомню, что во избежание путаницы в символах здесь и далее по тексту мнимая единица обозначается символом i, кроме отдельно оговариваемых мест.
Т. е., |
для комплексных амплитуд запаздывание во времени означает сдвиг |
||||||||||
по фазе ωr = kr = |
2π |
r . |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
v |
|
λ |
|
|
|
|
|
||||
Попутно заметим, что в соответствии с уравнением непрерывности |
|||||||||||
|
|
|
div j = − |
∂ρ |
, |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
∂t |
||
для линейных тока i и заряда τ, имеющего вид |
|||||||||||
|
|
|
|
d i |
|
= − |
d τ |
, |
|||
|
|
|
|
d l |
|
||||||
|
|
|
|
|
d t |
||||||
связь между током и зарядом в частотной области примет вид: |
|||||||||||
|
|
|
|
|
∂I |
=−iωτ. |
|||||
|
|
|
|
|
∂l |
||||||
|
|
|
|
|
|
|
|
|
|
||
8
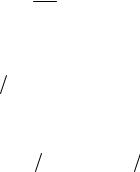
Таким образом,
– связь потенциалов A и ϕ позволяет решать уравнение Даламбера только для A , а ϕ находить по уравнению калибровки div A = −εµ ∂∂ϕt .
– можно вообще не искать скалярный потенциал ϕ, а по потенциалу A оп-
ределять H и уже по H находить E, интегрируя вторую формулу в системе
(15.1).
Теперь перейдем к определению электромагнитных полей элементарных излучателей.
3. Поле диполя Герца
Диполь Герца – модель, представляющая собой равномерное по длине l распределение тока, вызванного переменным во времени зарядом q на концах отрезка. При этом ток i связан с переменным зарядом выражением
i = − ∂∂qt .
Откуда, согласно выражениям (15.12) и (15.13):
A =µi(t − r v)l , |
|
|
|
|
|
|||
|
|
4πr |
|
|
|
|
|
|
ϕ = |
1 |
q(t |
− r1 |
v) |
− |
q(t − r2 |
v) |
, |
|
|
r1 |
|
r2 |
|
|||
|
|
|||||||
|
4πε |
|
|
|
|
|||
где r1 и r2 – расстояния, соответственно, от положительного и отрицательного зарядов до точки наблюдения M.
Причем, учитывая малость длины l , выражение для ϕ , стоящее в скобках, легко преобразовать с помощью формулы:
f ( t, r + ∆r) − f ( t, r ) = ∂ f (t,r) ∆r .
∂r
Поэтому
9

|
|
|
|
|
|
|
|
|
|
|
|
|
|
q ′( t −r |
|
) |
|
|
|
|
|
|
ϕ= |
|
1 ∂ |
q ( t − r |
v |
) |
∆r = |
1 |
|
− |
v |
− |
1 |
q (t − |
r |
|
∆r , |
||||||
|
|
|
|
|
|
|
|
) |
||||||||||||||
4 |
|
|
|
r |
|
|
|
vr |
|
|
r 2 |
v |
||||||||||
|
πε ∂r |
|
|
|
|
4 πε |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
r |
|
|
r |
где |
|
) |
есть производная по аргументу |
t − v или, что то же, по вре- |
|
q ( t − v |
|||||
Аz
zАθ
θ Аr
Аr
|
|
r2 |
|
|
–q |
θ |
r1 |
l |
r |
|
|
+q |
∆r |
|
|
|
|
x
α
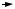 y
y
Рисунок 15.4 – Диполь Герца в сферической системе координат
мени, а отрезок ∆r , как видно из рис. 15.4 , равен ∆r =l cos θ.
Напряженности электромагнитного поля E и H можно вычислить, как отмечалось выше, различными способами. Покажем решение задачи последним из перечисленных, т. е. по A определим пространственное распределение вектора H и уже по H найдем пространственное распределение вектора E .
Согласно рис. 3.4
|
0 |
|
|
0 |
|
i(t − r |
v |
) l |
|
A = z |
Az |
= z |
µ |
|
|
. |
|||
|
|
4πr |
|
||||||
|
|
|
|
|
|
|
|
||
В сферической системе координат:
10
