АГ Векторная алгебра 2015-16 / 03 Базис и система координат

13

Базис и система координат

Базис и координаты вектора, единственность разложения вектора по базису

Определение 28

Базисом на плоскости называется пара линейно независимых векторов плоскости при условии, что любой вектор плоскости разлагается в линейную комбинацию этих векторов.

Утверждение 4

Любая пара неколлинеарных векторов плоскости может быть базисом этой плоскости.

Определение 29

Базисом в пространстве называется тройка линейно независимых векторов пространства при условии, что любой вектор пространства разлагается в линейную комбинацию этих векторов.

Утверждение 5

Любая тройка некомпланарных векторов пространства может быть базисом этого пространства.

Замечание 1

Далее все рассуждения для пространства справедливы также и для плоскости.

- векторы базиса (соответственно первый, второй, третий). Разложение вектора по базису:

(14)

- координаты вектора в базисе

(15)

Определение 30

Координаты вектора – коэффициенты разложения данного вектора по базису.

Теорема 8

Любой вектор разлагается по базису единственным образом.

♦ От противного:

Допустим и . Тогда

Из условия существования противоположного вектора, коммутативности сложения, дистрибутивности относительно сложения чисел получаем:

Система векторов - базис, поэтому линейно независима. Коэффициенты линейной комбинации могут быть только нулями. Поэтому . Следовательно, разложение единственно. ♦

Теорема 9 (свойства операций над векторами, заданными своими координатами)

1. Соответствующие координаты равных векторов равны.

(16)

2. При сложении двух векторов соответствующие координаты складываются.

(17)

3. При умножении вектора на число, его координаты умножаются на это число.

, (18)

♦

1) Необходимость. Допустим и . Из свойства коммутативности сложения векторов, дистрибутивности относительно сложения чисел получаем:

Линейная комбинация векторов равна нулю, т.е. эти вектора линейно независимы и коэффициенты линейной комбинации могут быть только нулями. Поэтому .

Достаточность. Если , то из следует

. ♦

Замечание 2

Коллинеарность двух векторов, заданных своими координатами

(19)

Линейная зависимость и независимость векторов, заданных своими координатами

Линейная зависимость двух векторов на плоскости, заданных своими координатами

, и линейно зависимые векторы на плоскости

Линейная независимость двух векторов на плоскости, заданных своими координатами.

, и линейно независимые векторы на плоскости

Линейная зависимость трех векторов в пространстве, заданных своими координатами

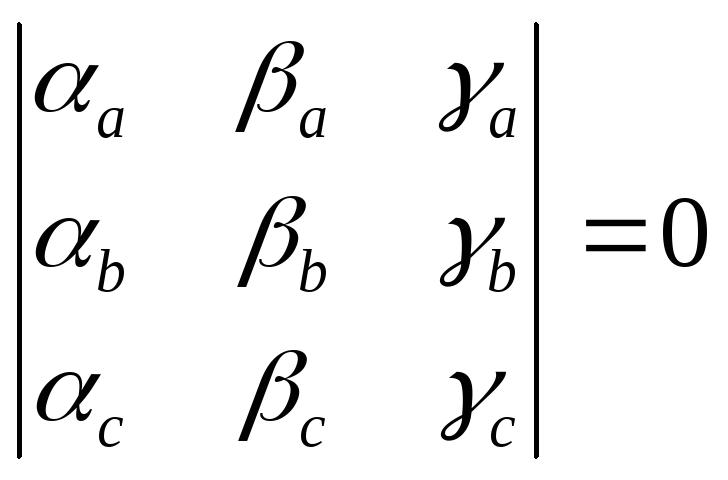
, и линейно зависимые векторы в пространстве.

Линейная независимость трех векторов в пространстве, заданных своими координатами.

, и линейно независимые векторы в пространстве

Аффинная система координат

Определение 31

АСК – совокупность базиса и точки, к которой приложены векторы базиса. О – точка, к которой приложены векторы базиса, есть начало АСК.

;

Определение 32

Радиус-вектор точки М – вектор, начало которого совпадает с началом АСК, а конец с т.М.

, (20)

где - коэффициенты разложения по базису.

O M

Определение 33

Координаты точки М в АСК - координаты в базисе данной АСК.

Простейшие задачи в АСК

Координаты вектора с заданным началом и концом:

A

O B

по правилу треугольника

В силу теоремы получаем:

.

Деление отрезка в данном отношении

Известны координаты т. А и В в некоторой АСК.

Дано: АСК;

A

M

B

O Найти: =?

Получаем

(21)

СВОДКА ФОРМУЛ

1) (22)

2) (23)

3) и линейно зависимые векторы на плоскости

(24)

4) и линейно независимые векторы на плоскости

(25)

5) ,и линейно зависимые векторы в пространстве

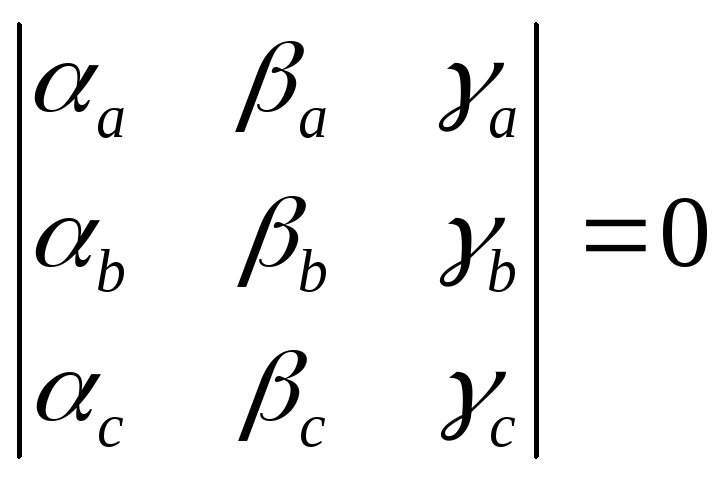(26)

6) , и линейно независимые векторы в пространстве

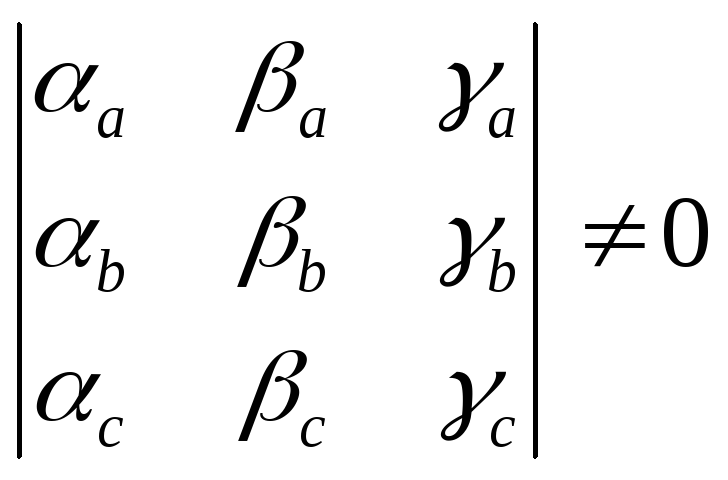(27)

Базис и аффинная система координат на прямой

Определение 34

Рассмотрим прямую и вектор на этой прямой. Этот вектор является базисом любых векторов, лежащих на этой прямой.

Определение 35

Прямая с фиксированным на ней вектором называется осью.

- ось

(28)

Определение 36

Ось с зафиксированным на ней началом координат называется числовой осью.

Проекция вектора на ось

Определение проекции

Проекция точки и проекция вектора на ось вдоль прямой на плоскости

Определение 37

Пусть дана ось l и прямая d, неколлинеарная l. Возьмём на плоскости точку М, проведём через неё прямую, параллельную прямой d. Она пересечёт l в точке М’.

Точка М’ называется проекцией т. М на ось l вдоль прямой d.

_d

_M`

_l

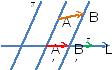
Определение 38

Пусть даны на плоскости вектор и ось l. Пусть дана прямая d , неколлинеарная l. Построим проекции точек А и В на оси l вдоль прямой d , получим точки А` и В`. Вектор _{называется векторной проекцией вектора} на ось l вдоль прямой d. Прямая d называется проектирующей.

Проекция точки и проекция вектора на ось вдоль плоскости в пространстве

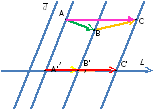
Определение 39

Проекцией точки М на ось l вдоль плоскости называется точка М’, где М’ – точка пересечения оси l с прямой, проходящей через точку М и параллельной плоскости .

M’

_M

_l

Определение 40

Проекцией вектора на ось l вдоль плоскости называется вектор , где А` - проекция т. А на ось l , а В` - проекция т. В на ось l вдоль плоскости - векторная проекция на ось. Плоскость называется проектирующей.

Определение 41 (численное значение проекции вектора на ось)

Координата вектора на оси l наз. числовой проекцией вектора на ось l – пр _l (29).

Свойства проекций

1. Проекции равных векторов

(30)

2. Проекция суммы векторов

(31)

3. Проекция произведения вектора на число

(32)

4. Ортогональная проекция вектора на ось и ее значение

(33)

- ортогональная проекция вектора на ось l,

• угол наклона к l.

Прямоугольная декартова система координат (ПДСК)

Прямоугольная декартова система координат как частный случай аффинной

Определение 42

ПДСК – АСК, у которой базисные векторы попарно перпендикулярны и модули базисных векторов равны. За единицу длины принимается длина базисного вектора. Базисные векторы ПДСК называются ортами и обозначаются . Базис в ПДСК при этом называется ортонормированным.

Определение 43

Орт – единичный вектор, имеющий направление.

Длина вектора, расстояние между точками в ПДС

Дан вектор , тогда длина вектора:

(34)

Даны две точки , тогда расстояние между точками:

(35)

Связь координат вектора и проекций вектора на оси в ПДСК

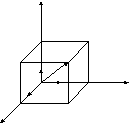
Теорема 10

Координаты вектора ПДСК равны проекциям этого вектора на соответствующие оси координат.

z

Z

A

О Y y

X

Доказательство.

Приложим вектор к началу координат и построим параллелепипед на осях, параллельных прямым.

Тогда – ортогональная векторная проекция вектора на ось x: .

Здесь X – координата на оси x в базисе i. По определению X – числовое значение проекции вектора на ось x:

.

Так как плоскости взаимно перпендикулярны и перпендикулярны осям, аналогично

, .

Направляющие косинусы вектора

Проекция вектора на направление

(36)

В ПДСК координаты вектора :

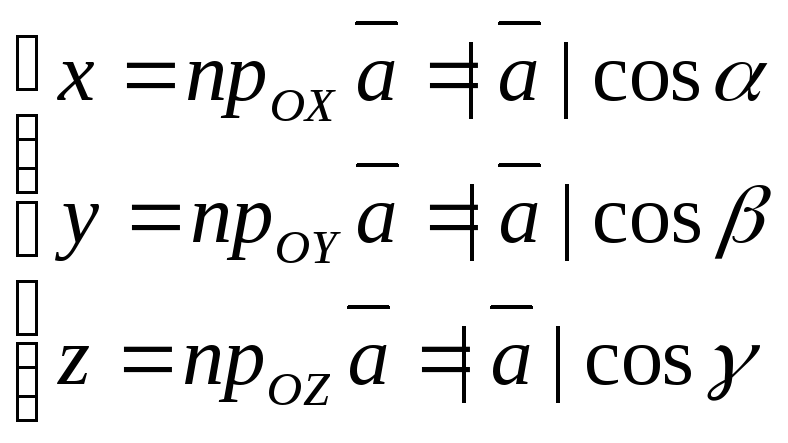(37)

углы между вектором и положительными направлениями осей OX,OY,OZ соответственно.

Ортом оси OX является вектор .

Ортом оси OY является вектор .

Ортом оси OZ является вектор .

Ось - абсцисса, ось - ордината, ось - аппликата.

Определение 44

(38)

- направляющие косинусы вектора .

Подставим эти преобразования в равенство , получим

(39).

Основное свойство направляющих косинусов вектора

Условие на направляющие косинусы

(40)

Вычисление направляющих косинусов вектора через его прямоугольные координаты

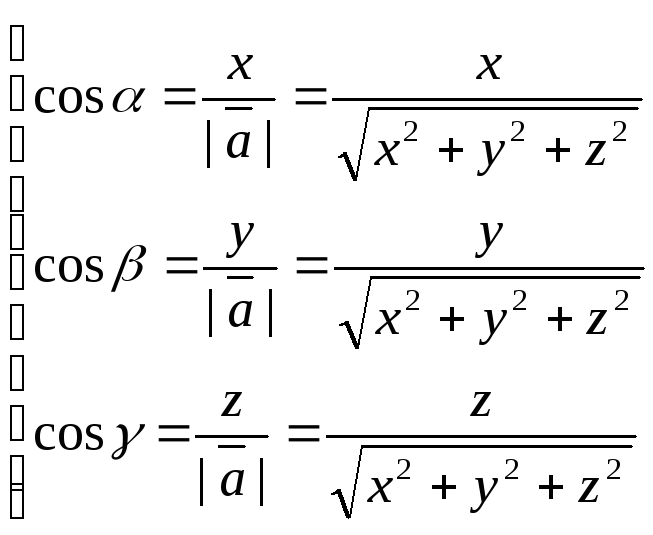. (41)