
АГ Векторная алгебра 2015-16 / 04 Скалярное произведение векторов
.doc
Скалярное произведение векторов
Определение скалярного произведения векторов
Определение 45
Скалярным произведением вектора
![]() на
на
![]() называется число, равное произведению
длин этих векторов на косинус угла
называется число, равное произведению
длин этих векторов на косинус угла
![]() :
:
![]() ,
(42)
,
(42)
где
![]() - наименьший угол между векторами
- наименьший угол между векторами
![]() и
и
![]() ,
приведённых к общему началу.
,
приведённых к общему началу.
Выражение скалярного произведения векторов через ортогональную проекцию вектора на направление другого вектора
![]() (43)
(43)
![]() (44)
(44)
Геометрические свойства скалярного произведения
1) Скалярное произведение перпендикулярных векторов
![]() (45)
(45)
2) Зависимость знака скалярного произведения от угла между векторами
![]() (46)
(46)
Доказательство:
-
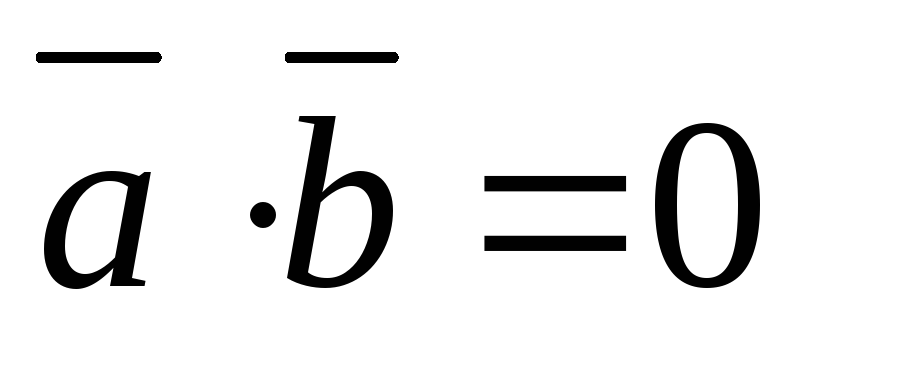

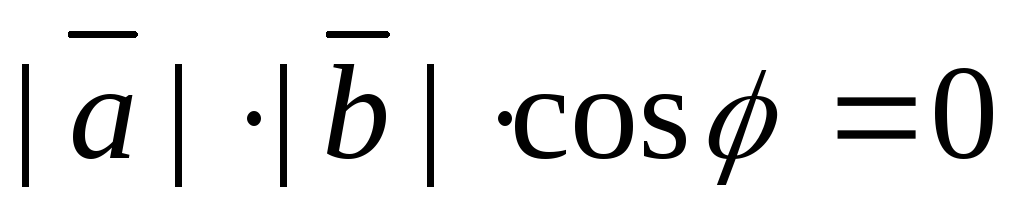

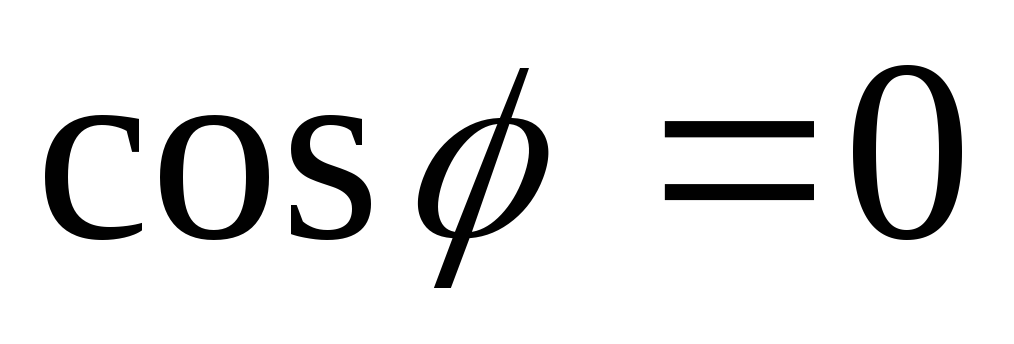

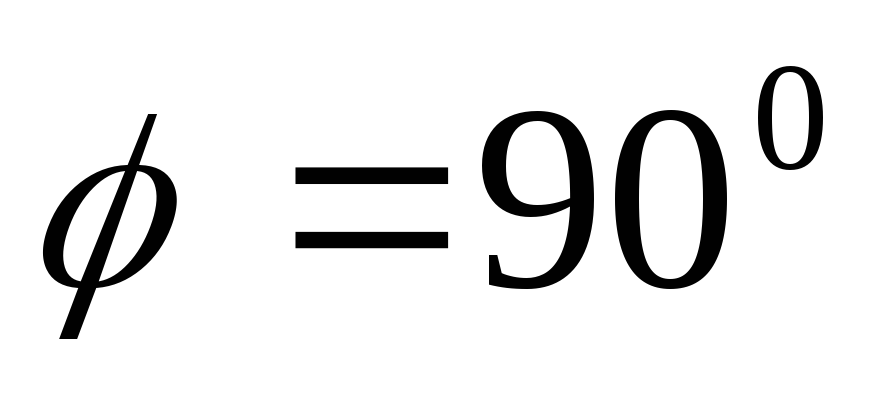

 .
. -


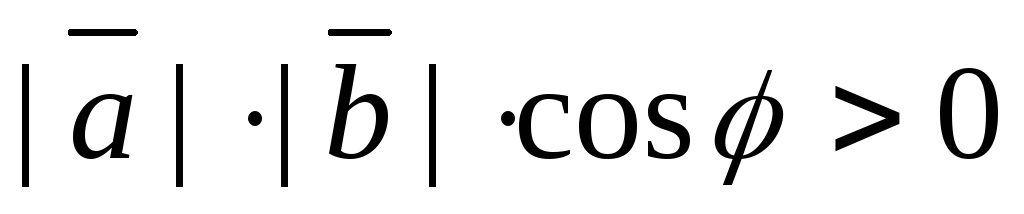

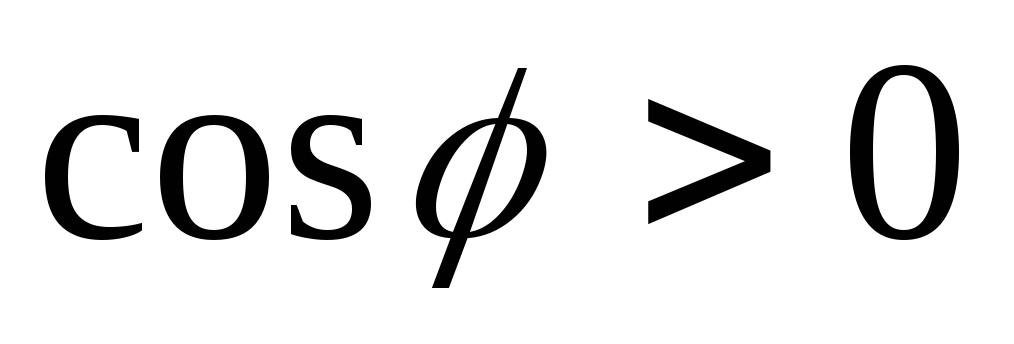

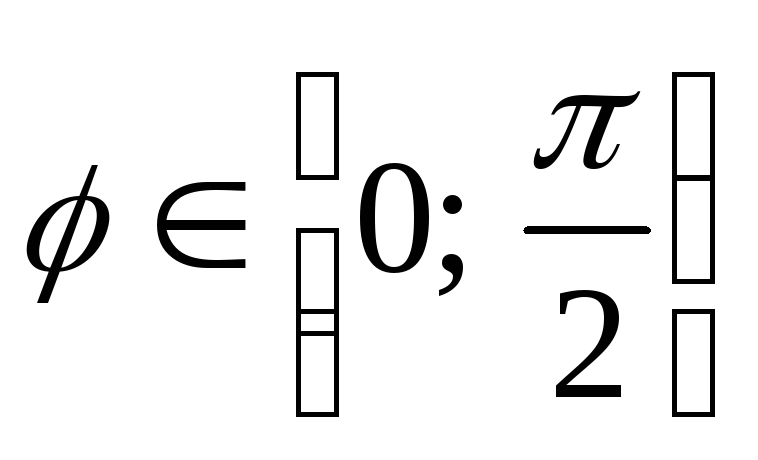
![]()
![]() – острый;
– острый;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – тупой.
– тупой.
Замечание
![]() (47)
(47)
Алгебраические свойства скалярного произведения
-
коммутативность
![]() (48)
(48)
-
дистрибутивность
![]() (49)
(49)
-
ассоциативность относительно умножения на число
![]() (50)
(50)
4)
![]() (51)
(51)
![]()
Доказательство:


![]()
![]() ;
;
![]()
Скалярное произведение векторов, заданных своими координатами в ПДСК
Пусть в ПДСК заданы координаты векторов
![]()
![]()
Теорема 11
Скалярное произведение двух векторов заданных координатами в ПДСК есть сумма произведений соответствующих координат:
![]() (52)
(52)
Доказательство:
![]()
Вследствие взаимной перпендикулярности векторов
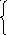
![]() .
.
![]() .
.
Из свойств скалярного произведения и
взаимной перпендикулярности
векторов: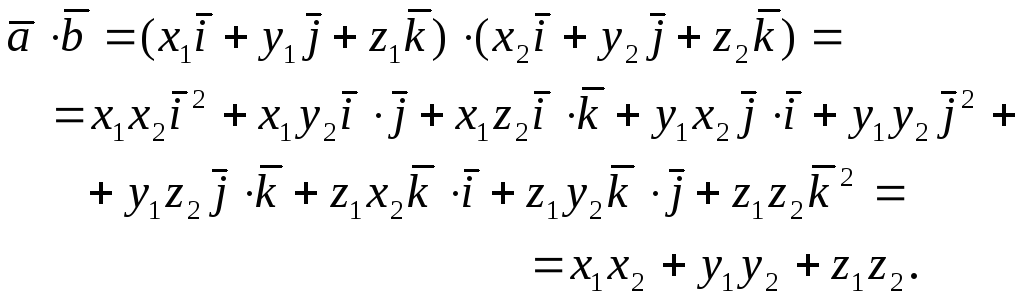 Пусть
в АСК заданы координаты
векторов
Пусть
в АСК заданы координаты
векторов
![]()
![]()
Тогда
![]()
Применение формулы вычисления скалярного произведения векторов, заданных своими координатами в ПДСК
Пусть в ПДСК заданы координаты векторов
![]()
![]()
-
Угол между векторами
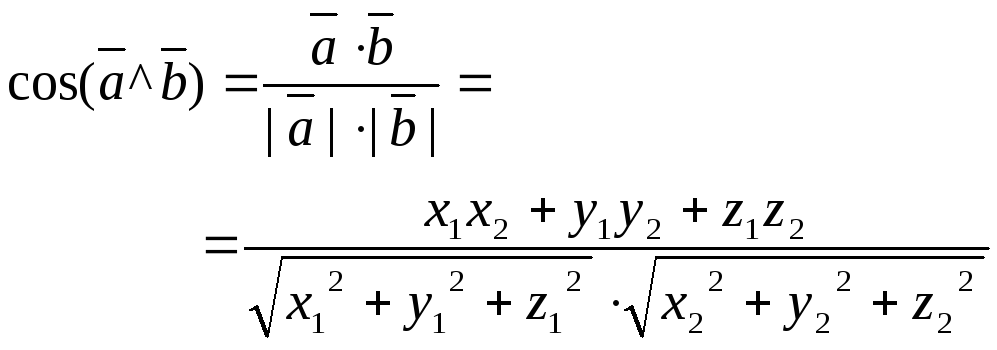 (53)
(53)
-
Длина вектора, расстояние между двумя точками
 (54)
(54)
-
Проекция вектора на направление другого вектора
![]()
![]() (55)
(55)
