
лекции ВТиИТ / 01_АЦП-ЦАП
.pdf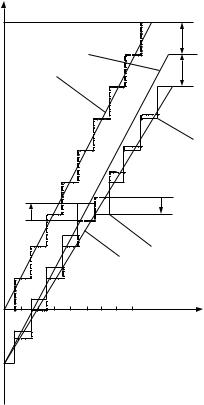
Цифро-аналоговые (ЦАП) и аналого-цифровые (АЦП) преобразователи
Как следует из названия, цифроаналоговые преобразователи преобразуют двоичный (или многозначный двоично-десятичный) код в пропорциональное значение напряжения или тока, аналого-цифровые выполняют обратное преобразование.
Оба этих преобразования имеют некоторые одинаковые особенности, к ним относится
шкала ЦАП и АЦП и Погрешности ЦАП и АЦП
Цифроаналоговые преобразователи бывают параллельного и последовательного (с широтно-импульсной (ШИМ) и частотно-импульсной модуляцией (ЧИМ)) типов.
Аналого-цифровые преобразователи бывают разных типов – параллельного,
последовательных приближений и интегрирующие.
Шкала ЦАП и АЦП
Как правило, нулевому значению двоичного кода соответствует нулевое значение аналогового тока или напряжения, коду состоящему из одних единиц – максимальное значение амплитуды аналогового сигнала. Обычно это значение определяется (а зачастую и равно) внешнему опорному напряжению Uоп
Если в двоичном числе n разрядов, то всего оно может иметь m=2n значений, тогда величина младшего значащего разряда будет равна Umax/2n, где Umax – максимальное аналоговое напряжение (опорное напряжение). В этом случае, если цифровой код равен k, то ему соответствует напряжение
U=kUmax/2n.
Кроме того, следует отметить, что некоторые преобразователи используют не только двоичный, но и (или) двоично-десятичный коды.
Если преобразователь может работать с отрицательными напряжениями, то отрицательные числа, как правило, бывают представлены в двоично-дополнительном коде.
Погрешности ЦАП и АЦП
Погрешность идеального преобразования определяется количеством разрядов в двоичном коде
ичасто определяется в МЗР – величине младшего значащего разряда.
Дополнительные погрешности реальных преобразователей определяются разными факторами
иимеют разный вид. На приведенном рисунке изображены передаточные характеристики для преобразователей с четырьмя основными типами погрешностей:
1.идеальная характеристика
2.погрешность сдвига (параллельный сдвиг характеристики вверх или вниз),
3.погрешность шкалы (изменение наклона),
4.нелинейность (неравномерность "ступенек"),
5.немонотонность (нелинейность, большая чем величина "ступеньки").
Uвых |
|
|
|
|
Uпш |
|
|
|
|
|
|
|
2 |
есм |
|
|
|
|
|
|
|
|
1 |
епш |
|
|
|
|
|
|
|
|
|
4 |
|
еj |
|
|
ej+1 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
3 |
|
|
|
|
D |
0 |
1 |
2 |
j |
j+1 |
|
Цифро-аналоговые преобразователи Параллельные ЦАП
Все параллельные ЦАП (в отличии от последовательных) имеют высокое быстродействие – от 0.1 до 10 мкс, высокой точностью – 10-14 двоичных разрядов, но должны быть реализованы в виде отдельных устройств (они допускают лишь аппаратную, но не программную реализацию).
Разновидности параллельных ЦАП
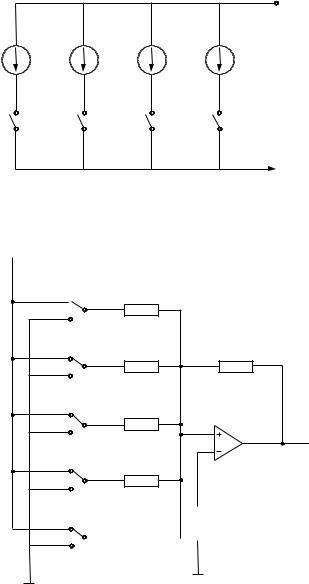
Схема с весовыми источниками тока
Схема с весовыми резисторами
Многозвенная цепная схема
Две последние разновидности ЦАП могут быть умножающими – в них опорное напряжение может изменяться в широких пределах и даже менять полярность. Такие ЦАП могут быть использованы в качестве усилителей или ослабителей аналогового сигнала, коэффициент передачи которого управляется двоичным кодом.
Кроме того, иногда в виде интегральной микросхемы выполняют не функциональнозаконченный ЦАП а только резисторную матрицу с ключами. В этом случае для построения полного ЦАП требуется внешний операционный усилитель.
Схема ЦАП с весовыми источниками тока |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
+Uкк Замыкание ключа, |
обозначенного |
цифрой 1, |
|||||
|
|
|
|
|
|
|
|
приводит к изменению выходного тока на одну |
||||||
|
1mA |
|
1/2mA |
1/4mA |
|
1/8mA |
|
единицу младшего значащего (нулевого) разряда, |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 - на |
одну |
единицу |
следующего разряда |
|||
|
|
|
|
|
|
|
|
(первого) и т.д. до старшего значащего разряда. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
a |
n-1 8 |
an-2 |
4 |
2 |
a0 |
1 |
|
an 1 |
2n 1 ... a0 20 |
ai 2i |
|
|||
|
|
|
|
|
|
|
|
i 0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Недостатком |
данной |
схемы |
является |
|||
|
|
|
|
|
|
|
IВЫХ |
сложность схем |
источников |
тока и |
трудность |
|||
|
|
|
|
|
|
|
создания умножающих ЦАП. В связи с этим |
|||||||
|
Старший разряд |
|
|
Младший разряд |
||||||||||
|
|
|
данная схема существенно менее распространена |
|||||||||||
|
|
|
|
|
|
|
|
|||||||
чем многозвенная цепная схема ЦАП типа R-2R или схема ЦАП с весовыми резисторами
Схема ЦАП с весовыми резисторами
Uоп
Старший разряд  an-1 R1
an-1 R1
R2 |
|
R6 |
|
|
|
|
|
|
R3
a1 R4
a0 |
R5 |
|
|
|
R7 |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Младший разряд
GND
GND
Замыкание ключа, обозначенного a0, приводит к изменению выходного напряжения на одну единицу младшего значащего (нулевого) разряда, a1 - на одну единицу следующего разряда (первого) и т.д. до старшего значащего разряда an-1.
Значения сопротивлений формируются как ряд: 20R, 21R, … 2n-1R
выходной ток:
|
U ОП a0 |
|
U ОП an 1 |
|
U ОП |
|
n 1 |
I |
... |
|
|
ai 2i |
|||
20 R |
2n 1 R |
2n 1 |
|
||||
|
|
|
R i 0 |
||||
Эта схема позволяет (в отличие от схемы с весовыми источниками тока) получать умножающие ЦАП, но имеет недостаток - сложность формирования большого числа прецизионных сопротивлений с сильно различающимся номиналом в составе одной микросхемы, этого недостатка лишена многозвенная цепная схема ЦАП (R-2R).
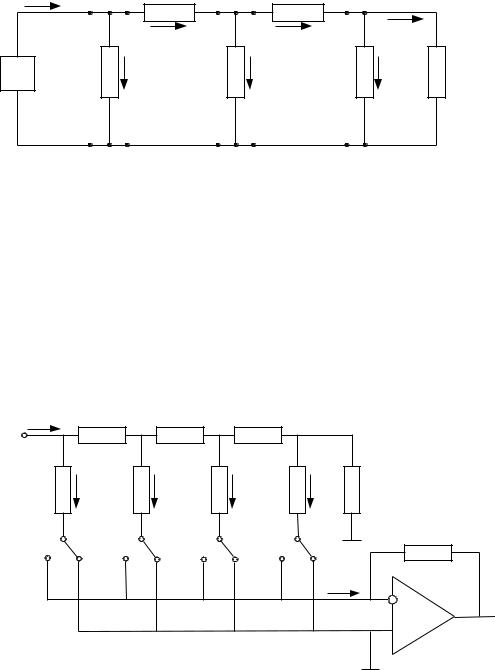
Многозвенная цепная схема ЦАП R-2R
Используется матрица сопротивлений R-2R. Особенностью такой матрицы является то, что для любого узла R-2R-R сумма сопротивлений справа и слева равна 2R.
|
I0 |
1 |
A |
2 |
R |
3 |
B 4 |
R |
5 |
C |
|
|
|
|
|
|
|||||||
|
|
|
|
|
I0/2 |
|
|
I0/4 |
|
I0/8 |
|
|
|
|
|
|
|
|
|
|
|
||
Uоп |
|
2R |
|
I0/2 |
|
2R |
I0/4 |
|
2R |
I0/8 |
2R |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
1' |
|
2' |
|
3' |
4' |
|
5' |
|
|
Входное сопротивление схемы правее точек 5-5` равно R, правее точек 4-4` равно 2R, правее точек 3-3` равно R, правее точек 2-2` равно 2R, правее точек 1-1` равно R. Таким образом, источник опорного напряжения Uоп в матрицу ток I0= Uоп/R. Так как сопротивление между точками 2-2` равно 2R, то в узле А ток I0 разветвляется в две ветви с равными сопротивлениями 2R. Следовательно, по первому (между точками 1-1`) резистору 2R будет протекать ток I0/2, и по резистору между точками 2-3 также будет протекать ток I0/2. Этот ток в узле В будет разветвляться в две ветви с одинаковыми сопротивлениями 2R. По второму (между точками 3-3`) резистору 2R будет протекать ток I0/4, и по резистору между точками 4-5 также будет протекать ток I0/4. Далее, ток в узле С будет разветвляться в две ветви с одинаковыми сопротивлениями 2R, со значением тока I0/8 в каждой ветви.
Таким образом, ток в ветви i можно определить как Ii = I0/2i = I0·2–i.
Матрица сопротивлений используется для построения ЦАП. Ниже представлена схема ЦАП на базе матрицы R-2R. Выходной ток матрицы подается на вход операционного усилителя, включенного по инвертирующей схеме.
Uоп |
I0 |
|
R |
|
R |
R |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2R |
I1 |
2R |
I2 |
2R |
Ii |
In-1 |
|
|
|
2R |
2R |
|||
|
a1 |
|
a2 |
|
ai |
an-1 |
Roc |
|
|
|
|
Iвх
Старший |
Младший |
разряд |
разряд |
Замыкание ключа а1, приводит к изменению выходного напряжения на одну единицу старшего значащего разряда, а2 - на одну единицу следующего разряда и т.д. до младшего
значащего разряда. |
|
|
|
Входной ток для операционного усилителя определяется |
как сумма токов, |
||
|
|
n |
n |
протекающих через сопротивления 2R и замкнутые ключи: Iâõ ai Ii |
I0 ai 2 i |
||
|
|
i 1 |
i 1 |
Выходное напряжение операционного усилителя, включенного по инвертирующей |
|||
схеме |
|
|
|
n |
Roc |
n |
|
Uâûõ IâõRîñ I0 Rîñ ai 2 i Uîï |
ai 2 i |
|
|
|
|
||
i 1 |
R i 1 |
|
|
Данная схема является, пожалуй, наиболее удачной и широко распространенной, поскольку:
в ней не используются сопротивления с сильно отличающимися номиналами как в схеме с весовыми резисторами и поэтому она более технологична при изготовлении ЦАП в виде интегральной микросхемы;
в отличие от схемы с весовыми источниками тока позволяет получать (при использовании в качестве ключей полевых транзисторов) ЦАП умножающего типа.
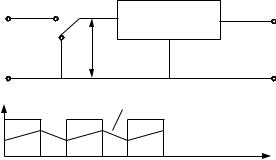
Последовательные или интегрирующие ЦАП
Собственно ЦАП данного типа представляет собой электрический ключ, периодически замыкаемый и размыкаемый, и формирующий импульсы. Преобразователи данного типа могут работать либо по принципу преобразования частоты формируемых импульсов в напряжение (ЧИМ), либо с широтно-импульсной модуляцией (ШИМ) - формируя сигнал.
После |
того, |
как |
сформирован |
импульсно |
|
s |
|
|||
модулированный |
сигнал, |
его |
|
достаточно |
|
|
Фильтр |
|||
|
|
|
|
|||||||
проинтегрировать |
|
(используя |
|
фильтр, |
Uоп |
U1 |
Uвых |
|||
подавляющий высокочастотную составляющую) |
||||||||||
|
|
|
||||||||
для получения среднего значения. В качестве |
|
|
|
|||||||
интегратора |
в таких |
ЦАП |
зачастую |
выступает |
|
|
Uвых |
|||
нагрузка. Лампа накаливания, нагревательный |
|
U1 |
||||||||
|
|
|||||||||
|
|
|
||||||||
элемент, |
коллекторный |
электродвигатель |
|
|
|
|||||
постоянного |
тока |
является |
прекрасными |
|
|
|
||||
интеграторами. |
tи |
Т |
2Т |
t |
|
|
|||
Для формирования импульсной последовательности |
с управляемой |
частотой или |
||
длительностью может быть применен таймер либо использована программная реализация этой задачи.
Последовательные ЦАП более медленные, чем параллельные, как правило менее точные, но существенно более дешевые поскольку в некоторых случаях вообще не требуют никаких дополнительных периферийных устройств кроме порта.
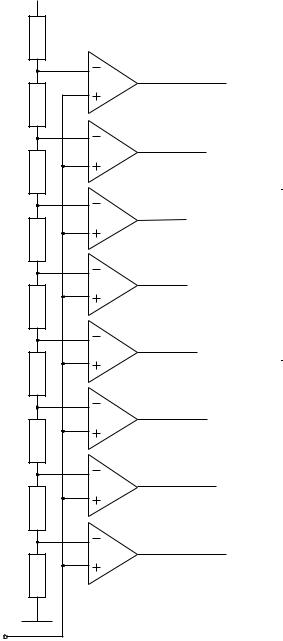
Аналого-цифровые преобразователи Параллельные АЦП
Uоп 
R1
DA1
R2
DA2
R3
DA3
R4
DA4
R5
DA5
R6
DA6
R7
DA7
R8
DA8
R9
Uвх
ОЗУ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A7 |
CD |
D0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
A6 |
|
D1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
A5 |
|
D2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Входной сигнал подается на неинвертирующие входы компараторов (DA1-DA8), соединенные параллельно. На инвертирующие входы этих компараторов подаются опорные напряжения с делителя напряжений на сопротивлениях R1-R9, на каждый компаратор подается опорное напряжение, отличающееся от соседних на шаг квантования. Количество включенных компараторов преобразуется в двоичный код при помощи шифратора СD.
Достоинства
-высокое быстродействие, достигающее десятков наносекунд.
Недостатки
-большая сложность (количество компараторов в схеме равно числу уровней квантования, и равно 2n где n - разрядность выходного кода
-высокая стоимость;
-невысокая точность (8-10 двоичных разрядов)
Особенности сопряжения с микропроцессорными системами
Поскольку такие АЦП более быстродействующие, чем микропроцессорная система, то данные сначала записываются с выхода АЦП в быстродействующее буферное

|
АЦП последовательных приближений |
|
||||||||
|
|
|
Uвх |
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
Uш |
|
|
|
|
“Пуск” |
|
1 |
|
|
|
|
Uвх |
|
|
|
|
|
|
|
|
|
|
|
||
|
Счетчик |
2 ЦАП |
|
|
|
|
|
|
|
|
G |
fт |
|
. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
Uкв |
|
“Стоп” |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
Uш – напряжение шкалы ЦАП, n – число разрядов счетчика и ЦАП, (2n – 1) – число тактов, за |
||||||||||
|
|
|
|
|
|
|
|
|
|
Uø |
которые достигается на выходе ЦАП Uш, тогда шаг квантования Uêâ |
2n 1 . |
|||||||||
Число тактов, за которое достигается Uвх равно |
U |
âõ |
U |
âõ |
(2n 1) |
|
|
|||
|
|
|
|
|
||||||
|
|
|
|
Uêâ |
|
|
Uø |
|
|
|
Время измерения Tèçì |
Uâõ (2n |
1) |
|
|
|
|
|
|
|
|
Uø fò |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
АЦП поразрядного взвешивания
Пуск |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ux |
|
|
|
|
|
|
|
|
|
|
|
||||
|
S |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
RG |
|
|
|
|
|
|
|
S |
T |
|
D0 |
|
D/A |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
D0 |
|
|
|
& |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
G |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
T |
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
& |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
Uш |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
T |
|
D2 |
|
|
|
|
8 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D2 |
|
|
|
& |
|
|
R |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
Ux |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Работа АЦП данного типа основана на алгоритме половинного |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
деления или дихотомии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
АЦП поразрядного взвешивания состоит из компаратора, на один |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
вход которого подается входное напряжение, |
а на другой - сигнал от |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
ЦАП. Схема из сдвигового регистра и блокировочных триггеров служит |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
для управления ЦАП - выработки последовательности кодов, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
приближений окончательного значения преобразования. |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Первое |
приближение |
равно половине максимального значения, |
|
|
|
|
|
|
|
|
Т |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
далее выясняется, больше входное напряжение этого значения или |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
меньше, в следующем цикле интервал в котором находится входное |
|
|
|
|
1 2 3 |
|
|
|||||||||||||||||||||||||||||||||||
напряжение делится еще пополам и т.д. Каждый цикл приближения дает один правильный двоичный разряд результата, начиная со старшего.
Достоинства и недостатки
Данный способ построения АЦП имеет по сравнению с интегрирующими и параллельными АЦП среднее быстродействие - типичное значение времени преобразования - 1...10 мкс, и среднюю точность - 10...14 двоичных разрядов. К недостаткам данного метода относится большая чувствительность к импульсным помехам, к достоинствам - хорошее согласование по времени измерения с типичными микропроцессорными системами, невысокая стоимость и сложность.
Интегрирующие АЦП
Общие особенности
АЦП данного типа осуществляют преобразование в два этапа.
На первом этапе входной аналоговый сигнал интегрируется и это проинтегрированное значение преобразуется в импульсную последовательность. Частота следования импульсов в этой последовательности или их длительность бывает промодулирована проинтегрированным значением входного сигнала.
На втором этапе эта последовательность импульсов преобразуется в цифровой код - измеряется ее частота или длительность импульсов.
Общие достоинства
АЦП данного типа нечувствительны к импульсным помехам.
АЦП данного типа нечувствительны к периодическим помехам если их период в целое число раз меньше периода интегрирования.
В результате, АЦП данного типа являются наиболее точными - типичная точность - 4...6 десятичных знаков, что соответствует 14...20 двоичным разрядам.
При работе АЦП данного типа в составе микропроцессорной системы возможна программная реализация части измерительной процедуры, а именно второго этапа - измерения временных характеристик последовательности импульсов, что упрощает преобразователь.
Общие недостатки
Преобразователи данного типа являются наименее быстродействующими из всех - типичное время преобразования - 1 - 1000 мс.
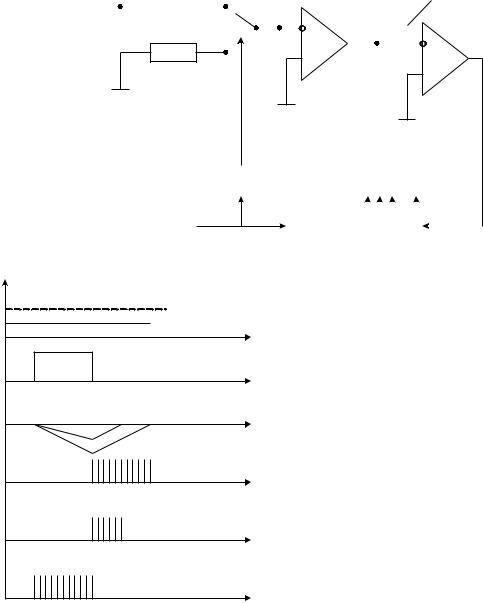
|
|
АЦП с двойным интегрированием |
||||||||||
|
|
Rэт |
|
|
|
|
|
С |
||||
UX |
|
|
|
|
|
|
|
|
|
|
нуль-компаратор |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rэт
Tи1
ФИ |
код |
|
|
|
пуск |
|
UUвх2 |
|
вх1 |
tи |
|
t1 |
t2 |
|
N2 |
|
N1 |
Nи |
|
|
|
|
|
|
|
|
|
стоп |
G |
|
счетчик |
||||||
|
|
|
||||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Это двухтактный преобразователь с заданной длительностью первого такта.
В течение первого такта происходит заряд интегрирующего конденсатора. Напряжение на нем в конце такта пропорционально интегралу входного напряжения.
Во время второго такта преобразования происходит разряд конденсатора заданным током до нулевого напряжения. Длительность этого такта и есть выходной сигнал преобразователя.
Достоинством данного варианта построения интегрирующего АЦП является не зависимость результата преобразователя от емкости интегрирующего конденсатора и пропорциональное изменение длительности второго такта при изменении длительности первого. Это позволяет снизить требования к точности тактовой частоты.
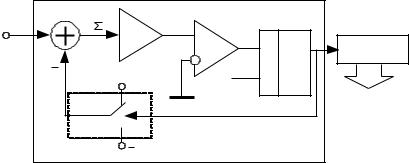
Сигма-дельта АЦП
Воснове идеи сигма-дельта АЦП лежит принцип одноразрядной дельта-модуляции, когда текущее значение сигнала сравнивается с предыдущим, и если сигнал превысил предыдущий отсчет на некое порогового значение, он кодируется 1, если уменьшился – 0. При этом предполагается, что входной сигнал остается неизменным во время всего цикла преобразований для одной выборки (выборка или отсчет – сформированное на выходе АЦП мгновенное цифровое значение измеряемого сигнала). Такая обработка требует достаточно больших скоростей дискретизации, как правило – в 20-40 раз выше максимальной частоты входного сигнала.
Впростейшем случае сигма-дельта АЦП включает в себя сигма-дельта модулятор, выполняющий преобразование аналогового сигнала в цифровую последовательность, и выходной фильтр (счетчик), преобразующий цифровую последовательность из модулятора в окончательный цифровой код.
Как и любой АЦП, сигма-дельта АЦП выдает оцифрованные значения сигнала в долях диапазона измерения. Измеряемый сигнал должен находиться в диапазоне опорного напряжения от +Uоп до –Uоп (относительно некоего установленного уровня "0", численно равного половине диапазона измерения). Если разрядность АЦП – m бит, то весь этот диапазон разбит на интервалы (кванты) 2Uоп/2m. Очевидно, что значения +Uоп и –Uоп могут быть любыми, не обязательно отрицательными. Для удобства рассуждений будем полагать, что уровень "0" соответствует напряжению 0 В.
Простейший сигма-дельта модулятор состоит из сумматора, интегратора, компаратора, триггера-защелки (D-триггера) и одноразрядного ЦАП. Одноразрядный ЦАП фактически представляет собой коммутатор, который в зависимости от входного сигнала (1 или 0) выдает напряжение +Uоп или –Uоп, соответственно.
Uвх |
|
U |
|
Uи |
|
|
|
+ |
|
|
D TT |
счетчик |
|
|
|
|
|
|||
|
|
|
+Uоп |
fmod |
C |
|
|
|
ЦАП |
|
|
К i |
код |
|
|
|
|
|
||
|
|
1-bit |
|
|
|
|
|
|
|
Uоп |
модулятор |
|
|
Перед началом вычисления новой выборки напряжения на выходе интегратора (Uи) и на выходе ЦАП равны нулю. Сигнал с выхода сумматора UΣ поступает на интегратор, где суммируется с предыдущим значением интегратора (т.е. для i-ой итерации Uи(i) = Uи(i–1) + UΣ. В начальный момент входной сигнал Uвх без изменений поступает на интегратор, поскольку на другом входе сумматора сигнал равен 0 (Uи(0) = Uвх).
Компаратор сравнивает выходное значение интегратора Uи с уровнем "0" и выдает 1, если Uи ≥ 0, и 0 при Uи < 0. Сигнал с компаратора поступает в выходной регистр, образуя последовательность одноразрядных цифровых отсчетов (выборка модулятора). Также этот сигнал попадает в ЦАП, который в зависимости от его уровня выдает +Uоп или –Uоп. В сумматоре это значение вычитается из входного сигнала Uвх и складывается с Uи в интеграторе. После чего процесс многократно повторяется.
Очевидно, что значение Uи в ходе оцифровки сигнала будет то нарастать, то убывать.
Например, если |
Uоп = 1 В, |
а Uвх = 0,6 В, то |
напряжение в |
интеграторе Uи будет |
|
последовательно |
принимать |
значения 0,6; |
0,6 + (0,6 – 1) = 0,2; |
0,2 + (0,6 – 1) = –0,2; |
|
–0,2 + (0,6 + 1) = 1,4; 1,4 + (0,6 – 1) = 1; 1 + (0,6 – 1) = 0,6 и т.д. Через пять итераций Uи будет |
|||||
равно Uвх = 0,6 |
В. На выходе компаратора |
и D-триггера |
при |
этом сформируется |
|
последовательность Ki=1101111011... В полученной последовательности присутствует циклически повторяющийся сигнал 11011. Для других значений входного сигнала число
символов в цикле (длина циклической последовательности) будет другим (см. таблицу). Нетрудно заметить, что если Uвх = –Uоп, то выходная последовательность будет состоять только из нулей, а если Uвх = +Uоп – только из единиц. При Uвх = 0 на выходе D-триггера будет 101010...
|
N такта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
UΣ, В |
0,5 |
-0,5 |
-0,5 |
1,5 |
-0,5 |
-0,5 |
-0,5 |
1,5 |
-0,5 |
-0,5 |
-0,5 |
1,5 |
-0,5 |
Uвх = 0,5В |
Uи, В |
0,5 |
0 |
-0,5 |
1 |
0,5 |
0 |
-0,5 |
1 |
0,5 |
0 |
-0,5 |
1 |
0,5 |
|
Ki |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
UΣ, В |
0,6 |
-0,4 |
-0,4 |
1,6 |
-0,4 |
-0,4 |
-0,4 |
-0,4 |
1,6 |
-0,4 |
-0,4 |
-0,4 |
-0,4 |
Uвх = 0,6В |
Uи, В |
0,6 |
0,2 |
-0,2 |
1,4 |
1 |
0,6 |
0,2 |
-0,2 |
1,4 |
1 |
0,6 |
0,2 |
-0,2 |
|
Ki |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
UΣ, В |
0 |
-1 |
1 |
-1 |
1 |
-0,3 |
-0,3 |
-0,3 |
-0,3 |
-0,3 |
-0,3 |
1,7 |
-0,3 |
Uвх = 0В |
Uи, В |
0 |
-1 |
0 |
-1 |
0 |
1,2 |
0,9 |
0,6 |
0,3 |
0 |
-0,3 |
1,4 |
1,1 |
|
Ki |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Математически механизм работы модулятора можно представить следующим образом. Пусть значение Uи в ходе преобразования k раз было меньше "0" и n раз больше или равным нулю; т.е. n + k = N, где N – общая длина кодовой последовательности для одной выборки. Очевидно, что Uи(N) = Uвх + n(Uвх – Uоп) + k(Uвх + Uоп); Uи(0) = Uвх.
Предположим, что через какое-то число итераций N ≠ 0 напряжение на интеграторе вновь принимает исходное значение: Uи(N) = Uвх. Тогда можно записать:
Uвх = Uвх (1 + n + k) + Uоп(k – n);
|
|
|
n k |
|
|
2n n k |
|
|
2n |
|
n k |
|
2n |
|
|
Uâõ |
U |
îï |
|
U |
îï |
|
U |
îï |
|
|
|
Uîï |
|
|
1 , или |
n k |
n k |
n k |
n k |
|
|||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|||||
|
U âõ |
|
1 |
|
|
|
|
U îï |
n |
|
|||
|
|
|
(1) |
|||
|
2 |
|
N |
|||
Таким образом, отношение числа единиц к общей длине циклической последовательности n/N однозначно определяет измеряемое напряжение Uвх как часть диапазона измерений Uоп.
Цикличность изменения напряжения в интеграторе обусловлена отрицательной обратной связью в сигма-дельта модуляторе. Длительность цикла зависит от соотношения значений Uвх, Uоп и точности их представления. Ее можно определить из формулы (1) при условии, что N и n – целые числа. Например, при Uвх = 0,7 В наименьшее значение N = 20, соответственно n = 17.
Если длина выборки сигнала в модуляторе достаточно велика, можно гарантировать, что она окажется в несколько раз больше самой длинной циклической последовательности N. Поэтому даже если она не кратна N, все равно "лишние" отсчеты (биты) существенно не исказят статистику и не повлияют на результат измерения Uвх.
Таким образом, с помощью всего лишь одноразрядного преобразования в заданном диапазоне напряжений можно измерить входной сигнал с любой точностью. Но очевидно, что чем выше точность, тем больше отсчетов необходимо в выборке модулятора для одного сигнала. И если частота следования многоразрядных выборок fs (т.е. скорость выдачи результатов измерения сигнала АЦП) должна удовлетворять теореме Котельникова и по крайней мере вдвое превышать ширину полосы частот сигнала F (fs > 2F), то частота одноразрядных отсчетов гораздо выше: fmod = Kfs, где К – коэффициент передискретизации (избыточной дискретизации). Коэффициент К может варьироваться в достаточно широких пределах, от единиц до тысяч. Именно этот факт и является одним из существенных ограничителей частотных свойств сигма-дельта АЦП, ставя в обратную зависимость их разрешение (число разрядов в выборке) и диапазон рабочих частот.
