Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория ФКП

.pdf

Скачиваний:

Добавлен:

13.03.2016

Размер:

1.54 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Р. М. Минькова

Функции комплексного переменного

и операционное исчисление

Рекомендовано методическим советом УрФУ в качестве учебного пособия для студентов,

обучающихся по программе бакалавриата и специалитета по направлениям подготовки 140800.62 – Ядерные физика и технологии;

141401.65 – Ядерные реакторы и материалы;

141405.65 – Технологии разделения изотопов и ядерное топливо;

140801.65 – Электроника и автоматика физических установок;

010900.62 – Прикладные математика и физика;

210100.62 – Электроника и наноэлектроника;

201000.62 –Биотехнические системы и технологии;

200100.62 –Приборостроение;

221700.62 – Стандартизация и метрология;

230100.62 – Информатика и вычислительная техника;

230400.62 –Информационные системы и технологии

Екатеринбург

УрФУ

2013

УДК 517.2: 517.3 ББК 22.161.1

М 62

Рецензенты:

кафедра прикладной математики Уральского государственного экономического университета (зав. кафедрой, доц., канд. физ.-мат. наук Ю.Б. Мельников);

старший научный сотрудник Института математики и механики УрО РАН,

проф., д-р физ.-мат. наук Е.Ф. Леликова;

Научный редактор − доц., канд. физ.-мат. наук Н.В. Чуксина

Минькова Р.М.

М 62 Функции комплексного переменного и операционное исчисление:

учебное пособие / Р.М. Минькова. Екатеринбург: УГТУ-УПИ, 2013. 72 с.

ISBN 978-5-321-01701-2

Рассмотрены функции комплексного переменного и операционное исчисление в объеме, необходимом при изучении специальных курсов. Изложение теоретического материала сопровождается решением примеров.

Учебное пособие предназначено для студентов физических и информационных специальностей физико-технического факультета.

Библиогр.: 10 назв. Рис.44.

Подготовлено кафедрой «Вычислительные

методы и уравнения математической физики»

при поддержке физико-технического факультета.

УДК 517.2: 517.3 ББК 22.161.1

ISBN 978-5-321-01701-2

1. Комплексные числа

Кратко напомним понятие комплексных чисел и действий с ними, которые рассматривались ранее.

1.1. Определение, изображение, формы записи

К понятию комплексного числа		привело	стремление	решить	уравнение
x2 1 0	и извлечь корень из отрицательного числа.

Комплексным числом z называется выражение вида				z x i y,	где x, y –
действительные числа, i − так называемая мнимая единица,				i2 1.
Числа x, y называются соответственно действительной				и мнимой частью
комплексного числа z и обозначаются		x Rez,	y Imz.
Если	x 0, то число 0 i y i y называется		чисто мнимым, если y 0, то
x i 0 x	есть действительное число.

Два комплексных числа считаются равными, если равны их действительные части и равны их мнимые части, т.е.

x1 i y1 x2 i y2 x1 x2, y1 y2.

Комплексные числа z x i y и z x i y, отличающиеся знаком мнимой части, называются комплексно-сопряженными.

Комплексное число z x i y изображают точкой М плоскости с координатами

x, y или ее радиус-вектором OM (рис. 1). Длина вектора OM назы-

M(x,y)

ваетсямодулем комплексногочисла z

иобозначается

или r :

x2 y2.

Угол

между

радиус-вектором

OM и

положительным

Рис. 1

направлением оси ох называют аргументом комплексного числа

Угол

определяется неоднозначно, с точностью до слагаемого 2 k k 0, 1, 2,... ; до-

говоримся брать то значение , которое заключено между

и , обозначать

его argz

и называть главным значением аргумента.

Наряду с алгебраической формой z x i y

комплексного числа рассмотрим

еще две формы записи.

Так как

x rcos ,

y rsin (рис.1),

то комплексное число

z x i y

можно

записать в тригонометрической форме: z r cos isin .

Введя функцию

ei cos isin , комплексное число можно записать в показательной форме: z r ei . Итак, имеем три формы записи комплексного числа

z x i y r cos isin r ei .

Пример 1.1. Записать комплексное число z 1 i3 в тригонометрической и показательной формах.

Решение. Чтобы записать z в тригонометрической форме, найдем его модуль и аргумент: z ( 1)2 ( 3)2 2, а для правильного отыскания аргумента ре-

комендуем изобразить число z									на плоскости (рис.							2). Найдем сначала острый
угол 1,	дополнительный					к		углу :		tg 1			3	,		1			. Тогда		y
угол 1,	дополнительный					к		углу :		tg 1		1		,		1		3	. Тогда	1 0			x
		2																		1 0			x
		2	; тригонометрическая и показательная формы за-																		1
			; тригонометрическая и показательная формы за-																		1
1	3																			z
	3
писи числа z 1 i					будут следующие:																	3
				3

															2		i				Рис. 2
							2			2					2						Рис. 2


			z	2 cos					isin		2 e					3 .
			z	2 cos		3			isin		2 e					3 .
						3				3

1.2. Основные действия c комплексными числами

Операции сложения, вычитания, умножения комплексных чисел определяются следующим естественным образом.

1). При сложении (вычитании) двух комплексных чисел складываются (соответственно вычитаются) их действительные и мнимые части, т.е.

z1 z2

x1 i y1 x2 i y2 x1 x2 i y1 y2 .

(1.1)

С геометрической точки зрения сложение (вычитание) комплексных чисел рав-

носильно сложению (вычитанию) изображающих их

векторов (рис.3). Отметим, что расстояние между

z1 z2

комплексными точками z1 и z2 равно

z1 z2

. Поэто-

му окружность с центром в точке z0 радиуса R имеет

уравнение

z z0

Рис. 3

2). Умножение двух комплексных чисел в алгеб-

раической форме определяется по правилам умножения двучленов с учетом

равенства i2 1, т.е.

(1.2)

z1 z2 (x1 i y1) (x2 i y2) (x1x2 y1y2) i(x1y2

x2y1)

При умножении двух комплексных чисел в тригонометрической форме их модули умножаются, а аргументы складываются; действительно:

z1 z2 r1 (cos 1 isin 1) r2 (cos 2 isin 2)

r1r2 (cos 1 cos 2 sin 1 sin 2) i(sin 1 cos 2 cos 1 sin 2)

r1 r2 cos( 1 2) isin( 1 2) .

Поэтому

	z1 z2		z1		z2	,	arg(z1 z2) argz1 argz2	.	(1.3)

В показательной форме

z1 z2 r1e i 1 r2 ei 2 r1r2 ei ( 1 2) .

3). Деление комплексных чисел определяется как действие, обратное умно-

жению, т.е. z z1 , если z z2 z1. Практически при делении двух комплексных z2

чисел в алгебраической форме нужно числитель и знаменатель дроби

(z2 0)

умножить на число,

сопряженное знаменателю;

тогда делителем

будет действительное число и

x1 iy1

(x1 iy1) (x2 iy2)

(x1x2 y1y2) i(y1x2 x1y2)

(1.4)

x2 iy2

(x2 iy2) (x2 iy2)

Например,

2 5i

(2 5i) (7 3i)

14 15i2 35i 6i

29 29i

i .

7 3i

49 9

(7 3i) (7 3i)

49 9i2

При делении двух комплексных чисел в тригонометрической и показательной формах их модули делятся, а аргументы вычитаются, т.е.

								z					z1	,					argz argz						argz		2	.	.		(1.5)
								z					z1	,					argz argz						argz			.	.		(1.5)
												z2												1
Действительно, если					z1	z,
							то z			1			z z				2	. Тогда					z			z		z	2	, argz	argz argz	2	.


					z2																		1							1
Отсюда		z1			z2
	z		,	argz argz					argz					2	.



		z2		1
		z2

											z					r1 ei 1					r1	e i
В показательной форме:													1											(	1	2).
В показательной форме:											z		2			r e			i 2		r				1	2).
													2			r e				2
															2

4). Возведение в степень комплексного числа в алгебраической форме осуществляется по правилам возведения в степень двучлена с учетом того, что


i2 1, i3 i2 i i,	i4 i2 i2 1 и т.д. Например, используя формулу для куба
разности, получим:	(2 i)3 23 3 22 i 3 2 i2 i3 8 12i 6 i 2 11i.
При возведении комплексного числа z		в большую степень удобно ис-
пользовать его тригонометрическую форму		z r cos isin . Учитывая, что

при умножении модули умножаются, а аргументы складываются, получим формулу Муавра:

zn rn (cosn i sinn ) rnein .

Пример 1.2. Вычислить z6 , если z 3 i.

Решение. Изобразим комплексное число z на плоскости (рис. 4), найдем его модуль и аргумент:

z	r		2 12 2,	tg	1	,		.
		3

				3			6

Тогда z6 r6(cos6 i sin6 ) 26(cos isin ) 64.

(1.6)

1 z

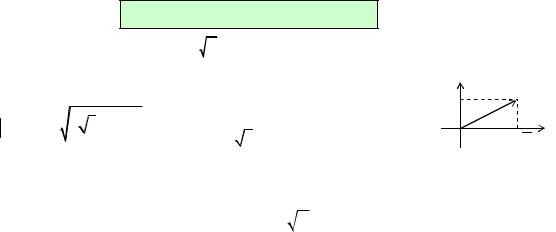
0 3

Рис. 4

5). Извлечение корня n-й степени из комплексного числа определяется как действие, обратное возведению в степень, т.е. n z w, если wn z .

При извлечении корня из комплексного числа z удобно использовать тригонометрическую форму записи комплексного числа. Пусть z r(cos isin ), w (cos isin ). Так как wn z, то

n(cosn i sinn ) r(cos i sin ).

У равных комплексных чисел модули должны быть равны, а аргументы могут отличаться на число, кратное 2 , то есть

n r, n 2 k

или n

2 k

Подставляя эти значения в выражение n

w (cos isin ), получим

2 k

cos

sin

(1.7)

k 0,1,2,...,n 1.

Придавая k

значения 0,1,2,...,n 1, получим n

различных значений корня n−й

степени из комплексного числа.

При других значениях

k получим значения

корня,

совпадающие с уже найденными. Например, при k n

и при k 0 значе-

ния корней совпадают:

w n

cos

2 n

sin

2 n

cos

i sin

cos

i sin

w .

Аналогично,

wn 1 w1 ,

wn 2 w2 ,....

Итак, для любого z 0

корень степени n из числа z имеет n различных значений.

Пример 1.3. Решить уравнение z3 1 0.

Решение. Из уравнения имеем z 3

Найдем модуль и аргумент числа −1:

arg 1 . Тогда корни уравнения имеют вид:

z 3 1 3cos i sin cos 32 k isin 32 k .

Придавая k значения 0,1,2, получим три корня уравнения:																			y
																			z0
									1				3						z0
	z0 cos		3		isin				2	i				,
			3			3			2		2							600
	z1 cos isin 1,															z1		600			x
																		1
	z2 cos			5		isin		5			1	i		3	.			1
				5				5			1			3
			3					3			2
			3					3			2			2					z	2
Эти корни лежат на единичной окружности и делят ее на три																			z
																		Рис. 5

равные части (рис. 5).


Если нужно извлечь корень квадратный, то можно и не пользоваться
формулой (1.7). Например,

							12i (3i)2 22 (2 3i)2 (2 3i).
	12i 5	12i 9 4					12i (3i)2 22 (2 3i)2 (2 3i).
Если вы не догадались о таком способе,														то можно обозначить					x i y		и
Если вы не догадались о таком способе,														то можно обозначить			12i 5		x i y		и

возвести это равенство в квадрат: 12i 5 x i y 2 x2 2ix y y2.

Приравнивая действительные и мнимые части, получим:

	2	y	2	5,		2	6	2		4		2
x		y		5,	x	2	6		5 x	4	5x	2	36 0.

	2x y 12,						x	2
	2x y 12,						x	2

Действительные корни получившегося биквадратного уравнения x 2. Тогда y 3 и z x i y (2 3i).

2. Функции комплексного переменного

Если каждому комплексному числу z из множества D соответствует комплексное число w из множества E, то w является функцией переменной z: w f z . При этом D есть область ее определения, а E − множество ее значений.

Мы будем рассматривать как однозначные, так и многозначные функции, т.е. каждому значению аргумента соответствует одно или много значений функции.


Например, функция w		3z i		определена при z i и является однозначной
Например, функция w		z2 1		определена при z i и является однозначной
		z2 1
функцией; функция w 5			z	является пятизначной функцией; функция
w Argz argz 2 k	k 0, 1, 2,... является многозначной функцией.
В дальнейшем	нам нужно будет выделять у функции ее действительную и

мнимую части. Как это делается, рассмотрим на примере функции w z2 . Так


как z x	iy, то	w x iy 2 x2 y2 2xyi.		Таким образом, функция w z2 пред-
ставлена	в виде	w u x,y i v x,y , где		u x, y x2 y2 − ее действительная
часть, а v x, y 2xy − ее мнимая часть.
Аналогичным образом любую функцию f z можно представить в виде

			f z u x,y iv x, y ;
			u x, y Re f z , v x,y Im f z .

2.1. Элементарные функции

Функции e z, sin z, cosz

Известно, что функции ez, sin z, cosz для любого действительного

z пред-

ставимы в виде суммы следующих рядов:

ez 1

(2.1)

sin z

(2.2)

cosz 1

(2.3)

Нетрудно показать, пользуясь признаком Даламбера, что эти ряды сходятся и для любого комплексного числа z. Поэтому формулы (2.1), (2.2), (2.3) естественно взять за определения функций ez, sin z, cosz для любого комплексного числа z. Заметим, что функции sinz, cosz нельзя определять, как в тригонометрии, т.к. угол z неможетбытькомплексным.Поэтомуипришлосьприбегнутьк помощи рядов.

Так как ряд для sin z	содержит только	нечетные степени z, то
sin z sin z , т.е. функция sin z	− нечетная. Ряд для cosz содержит только чет-
ные степени z, поэтому cos z cosz и функция cosz		– четная.

Связь между функциями e z, sin z, cosz

I). Запишем функцию ei z :

eiz 1 iz	iz 2		iz 3		iz 4		iz 5
	2!		3!		4!		5!

Сгруппируем слагаемые, стоящие на нечетных местах, и отдельно слагаемые, стоящие на четных местах, и учтем, что i2 1, i3 i , i4 1, i5 i, …:

eiz 1 z2!2 z4!4 i z 3!z3 5!z5 .

Сумма первого ряда равна cosz , сумма второго ряда равна sin z. Поэтому

eiz cosz isinz.

(2.4)

2). Заменяя в формуле (2.4) z

на z

и используя четность функции cosz и не-

четность функции sin z, получим

e i z cosz isinz

(2.5)

Складывая и вычитая формулы

(2.4)

и (2.5),

получим:

ei z e i z 2cosz ,

ei z e i z 2isinz , или

cosz

eiz e iz

sinz

eiz e iz

(2.6)

Формулы (2.4), (2.6) устанавливают связь между функциями e z, sinz, cosz и

называются формулами Эйлера.

Свойства функций e z, sinz, cosz

1). e z1 z2 e z1 ez2 .

Действительно, используя определение функции ez , получим

			z1				2				3		4								z2					2		z2	3			4
ez1 ez2 1			z1			z1			z1			z1							1		z2			z2				z2			z2
ez1 ez2 1																			1
		1!			2!			3!					4!							1!					2!		3!			4!

	z z			2		z	2	2z z				z			2		z		3	3z 2z		2	3z z 2						z			3
1	1			2	1						1 2			2				1		1		2					1 2			2			...
1		1!								2!													2!										...
		1!								2!													2!
	z z				z z						2		z z				2	3					z			z
	1			2			1	2						1			2			... e			z			z
	1			2																			1			2
1		1!						2!							3!												.
2). Функция e z		имеет период
2). Функция e z		имеет период														T 2 i.

Действительно, используя предыдущее свойство, а затем формулу (2.4), получим

ez 2 i ez e2 i ez cos2 isin2 ez . 3). Функции sin z, cosz имеют период T 2 .

Действительно, используя формулу (2.6) и периодичность функции ez , получим

		cos z 2						ei z 2				e i z 2						eiz e iz	cosz .
		cos z 2																	cosz .
												2					2
Аналогично проверяется периодичность функции sin z.
4). а) sin2 z cos2 z 1,
б) sin z	z		2		sin z		cosz		2	cosz sin z				2	,		г) sin2z 2sin z cosz ,
1			2			1			2			1		2			д) cos2z cos2 z sin2 z.
в) cos z		z		2		cosz cosz				2	sin z		sin z		2	,	д) cos2z cos2 z sin2 z.
1				2			1			2		1			2

Для проверки первых трех формул нужно записать sin z, cosz по формулам Эйлера (2.6). Следующие две формулы получаются из предыдущих при z1 z2.

5). Функции sin z, cosz − не ограничены на комплексной плоскости.

Например, cos in	ei in e i in		en e n	при n .

2		2

Обратим внимание, что свойства I), 3), 4) функций ez , sin z, cosz такие же, как для соответствующих функций действительной переменной. Свойства же 2)

и5) имеют место только для функций комплексной переменной. Перечисленные свойства используются при вычислении значений функций

e z, sin z, cosz и при решении уравнений, содержащих эти функции. Пример 2.1. Вычислить e3 i.

Решение. По свойству 1) и формуле (2.1): e3 i e3 e i e3 cos isin e3.

Гиперболические функции

Для комплексного аргумента гиперболические синус и косинус вводятся так же, как для действительного аргумента, т.е.

	shz ez e z	,	chz	ez e z	.	(2.7)

	2		2
Перечислим свойства функций shz,			chz .

1). Функции shz, chz имеют период 2 i (так же, как функция ez ).

2). Для комплексного аргумента существует следующая связь между тригонометрическими и гиперболическими функциями:

cos iz chz,

sin iz ishz,

(2.8)

ch iz

cosz,

sh iz isinz.

Проверим одну из этих формул:

cos iz

ei iz e i iz

ez e z

ch z .

3). Для комплексного аргумента (как и для действительного):

ch2 z sh2 z 1,

sh z1 z2 sh z1 ch z2 ch z1 shz2,

ch z1 z2 ch z1 chz2 shz1 shz2,

sh2z 2sh zch z,

ch2z ch2 z sh2 z.

Пример 2.2. Вычислить: а) sh 2 i

, б) ch i, в) cos 2 iln2 .

Решение. а) sh

i isin i;

б)

ch i cos 1;

cos

sin

в) cos 2 iln2

2 cos iln2

2 sin iln2 sin iln2 ish(ln2)

eln2 e ln2

2 2 1

Логарифмическая функция

Логарифмическая функция вводится как обратная к показательной, т.е. w Ln z, если z ew.

Пусть w u iv. Так как z ew , то z eu iv eu eiv ; отсюда z eu cosv isinv .

Мы получили тригонометрическую форму записи числа z, где eu – его модуль,

а v – его аргумент, или отличается от аргумента на 2πk. Таким образом, eu z

или u ln z ; v argz 2 k . Поэтому для вычисления Ln z u iv получаем сле-

дующую формулу:

Ln z ln	z	i arg z 2 k ,	k 0, 1, 2,	(2.9)

Значение этой многозначной функции при k 0 называют главным значением логарифма и обозначают ln z .

На функцию Ln z распространяется ряд свойств логарифма действительного переменного:

I) Ln z z		Ln z Ln z		,	2) Ln		z1	Ln z Ln z		,
	2		2						2
1		1						1
3) Ln z1z2 z2 Ln z1,						z2
					4) eLnz z .

Докажем, например, первое свойство:

Ln z1 z2 ln

z1 z2

iArg z1 z2

i Argz1 Argz2

Argz1 ln

iArgz2

Lnz1 Lnz2.

Пример 2.3. Вычислить ln 1 i

Решение.Найдёммодульиаргументкомплексногочисла z 1 i3 (см.пример1.1):


	z	2,		argz	2	.

					3
Тогда по формуле (2.9) имеем:
				ln2 i 23 .
ln 1 i
			3

Обобщенные степенная и показательная функции

Степенная функция w z a с произвольным комплексным показателем a i определяется равенством

		w z a eLnza e a Lnz			.
Показательная функция w a z			с произвольным комплексным основани-
ем a i определяется равенством

		w a z eLna z		e z Lna	.
Пример 2.4. ii eiLni ei ln1 i /2 2 k			e /2 2 k .
Обратные тригонометрические и гиперболические функции
По определению
w Arcsin z, если sinw z;			w Arccosz,			если cosw z ;
w Arctgz,	если tgw z ;		w Arcctgz ,			если ctgw z ;
w Arcsh z ,	если shw z ;		w Arcch z ,			если chw z ;
w Arcth z ,	если thw z;		w Arccth z ,			если cthw z.

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2018101.53 Кб14Теория управления. Амбарова.docx
#
25.12.2018440.83 Кб15Теория управления. Шпаргалка_РИОР, 2010 -36с.doc
#
22.02.201543.52 Кб28Теория управления1.doc
#
16.09.2019152.58 Кб18Теория фазовых переходов.doc
#
22.02.2015165.93 Кб15теория физика 2 курс 2 семестр.docx
#
13.03.20161.54 Mб70Теория ФКП.pdf
#
13.03.201632.35 Кб35Теория Холла.docx
#
01.03.20253.28 Mб0Теория(30 вопросов).doc
#
23.02.20151.91 Mб95Теория(30 вопросов).pdf
#
31.08.2019109.06 Кб4теорю концепц. граф. диз. 60 - 80е.doc
#
01.04.20253.04 Mб2Теософский словарь.doc