ТЕСТ В СУББОТУ ПО ТЕРМЕХУ

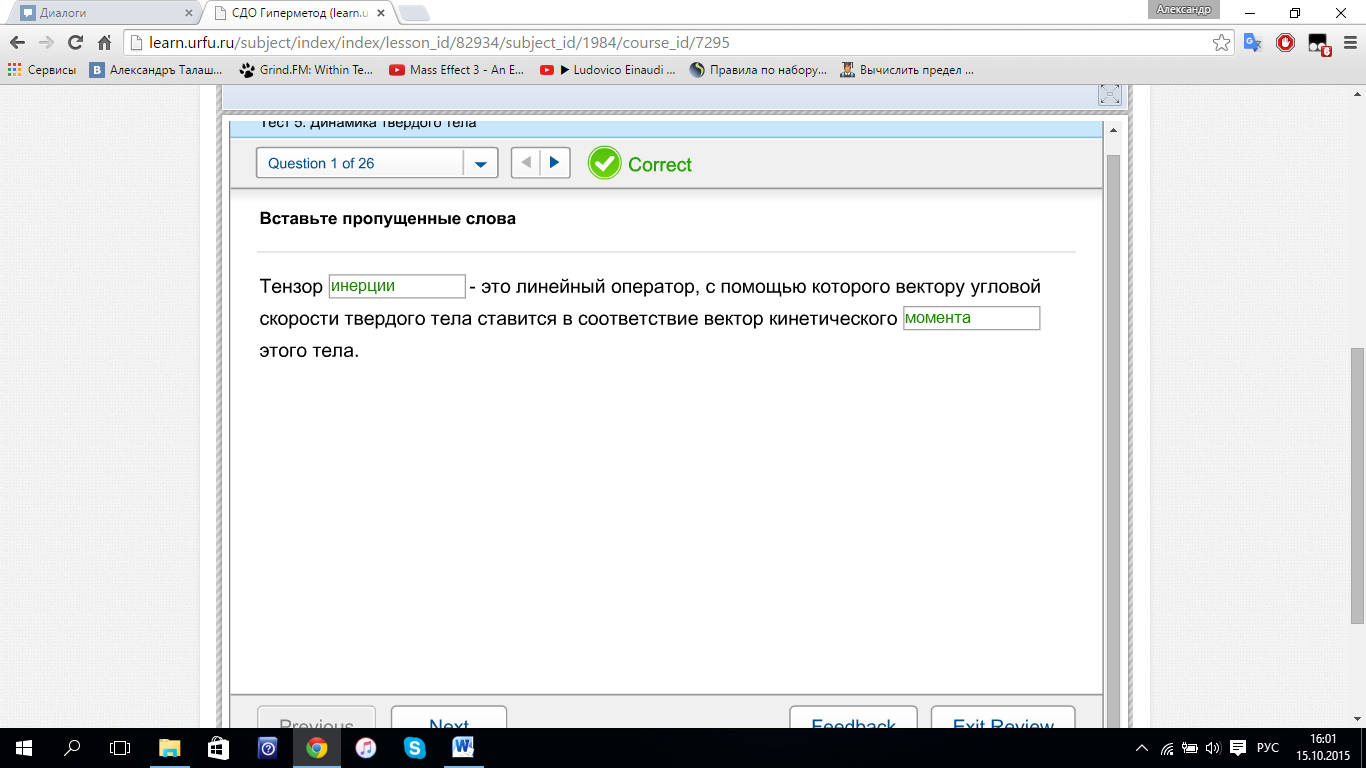Тензор ИНЕРЦИИ – это линейный оператор, с помощью которого вектору угловой скорости твердого тела ставится в соответствие вектор кинетического МОМЕНТА этого тела.Матрица тензора инерции имеет вид (верно)Матрица тензора инерции имеет вид (неверно)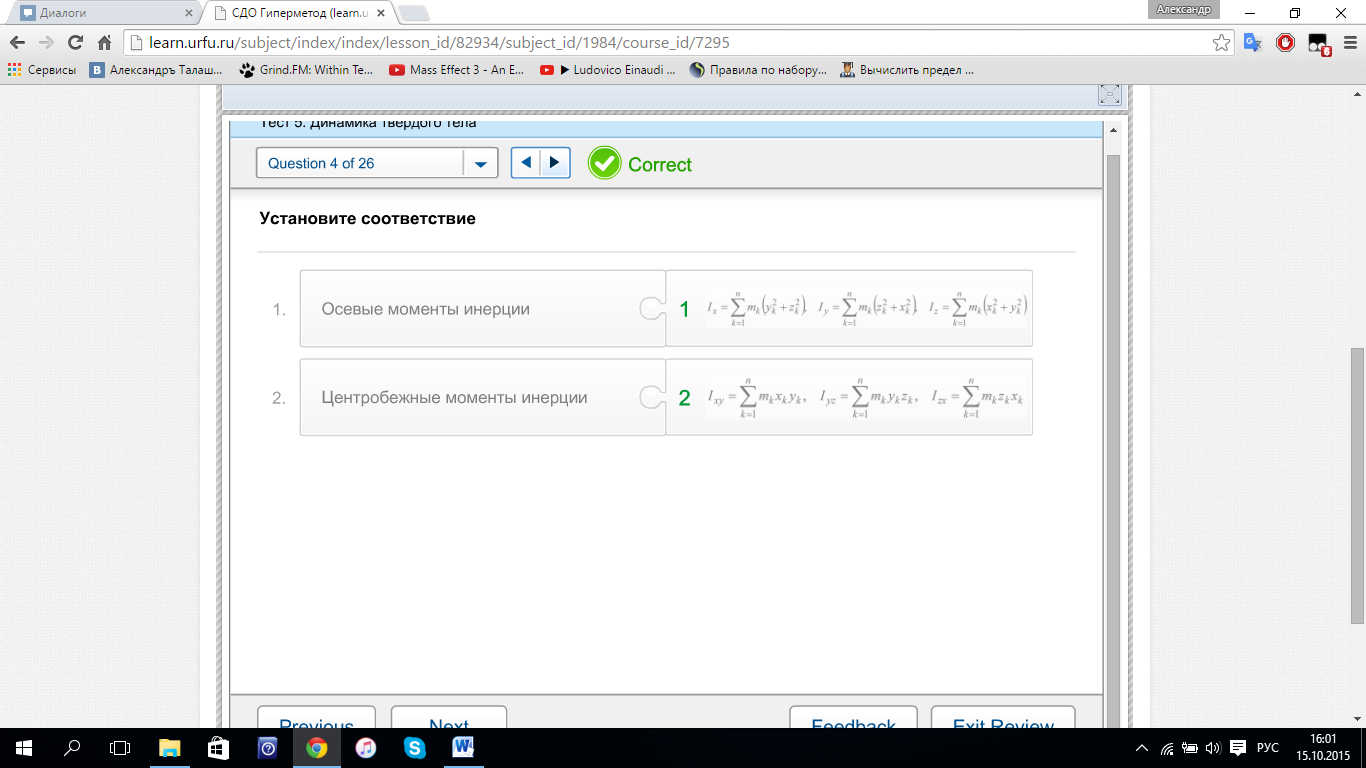Установите соответствие (осевые моменты инерции)Главными осями ИНЕРЦИИ называются оси координат, в которых матрица тензора инерции имеет диагональный вид. Если начало координат совпадает с центром масс, то она называются главными ЦЕНТРАЛЬНЫМИ осями инерции.Установите соответствие (Матричное преобразование тензора инерции при переходе к новому базису)Установите соответствие (Динамические уравнения вращения твердого тела вокруг неподвижной оси)Установите соответствие (Кинетическая энергия тела при его сферическом движении)Динамические уравнения Эйлера допускают аналитическое интегрирование при произвольных начальных условиях в случаях ЭЙЛЕРА-Пуансо, Лагранжа-Пуассона, КОВАЛЕВСКОЙ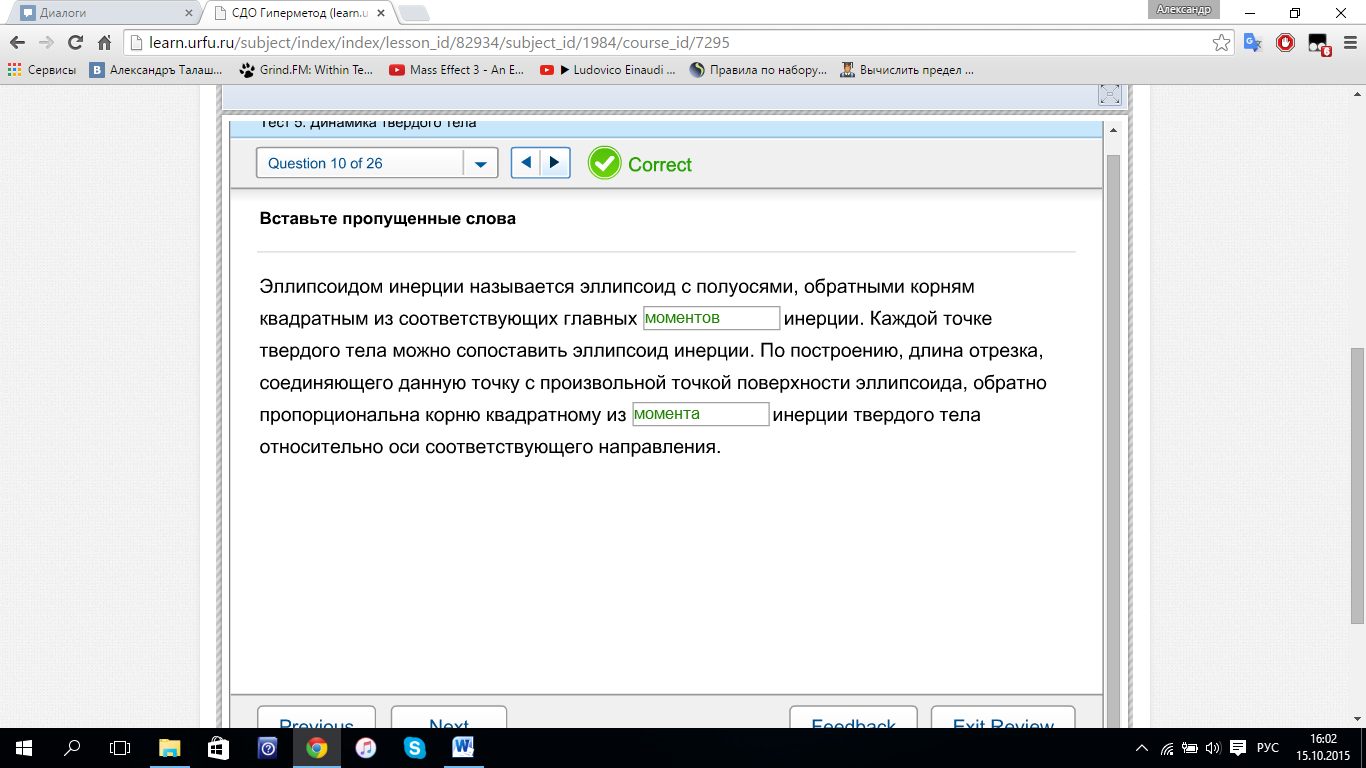Эллипсоидом инерции называется эллипсоид с полуосями, обратными корням квадратным из соответствующих главных МОМЕНТОВ инерции. Каждой точке твердого тела можно сопоставить эллипсоид инерции. По построению, длина, отрезка, соединяющего данную точку с произвольной точкой поверхности эллипсоида, обратно пропорциональна корню квадратному из МОМЕНТА инерции твердого тела относительно оси соответствующего направления. Теорема Гюйгенса-Штейнера: Момент инерции относительно произвольной оси равен моменту инерции относительно ПАРАЛЛЕЛЬНОЙ оси, проходящей через центр масс, сложенному с произведением МАССЫ тела на квадрат расстояния между осями.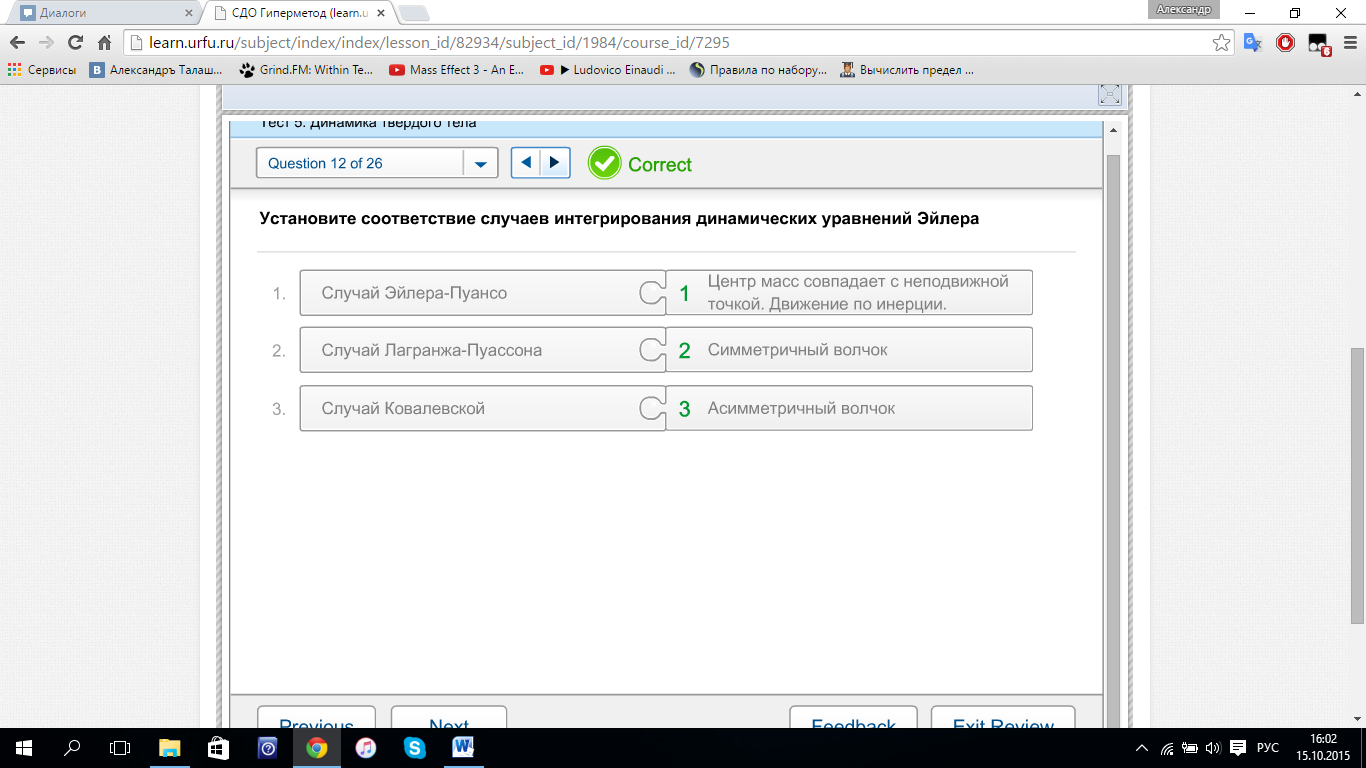Установите соответствие случаев интегрирования динамических уравнений ЭйлераУстановите соответствие общих интегралов динамических уравнений Эйлера в случае Эйлера-ПуансоДифференциальные уравнения свободного движения твердого тела имеют вид (верно)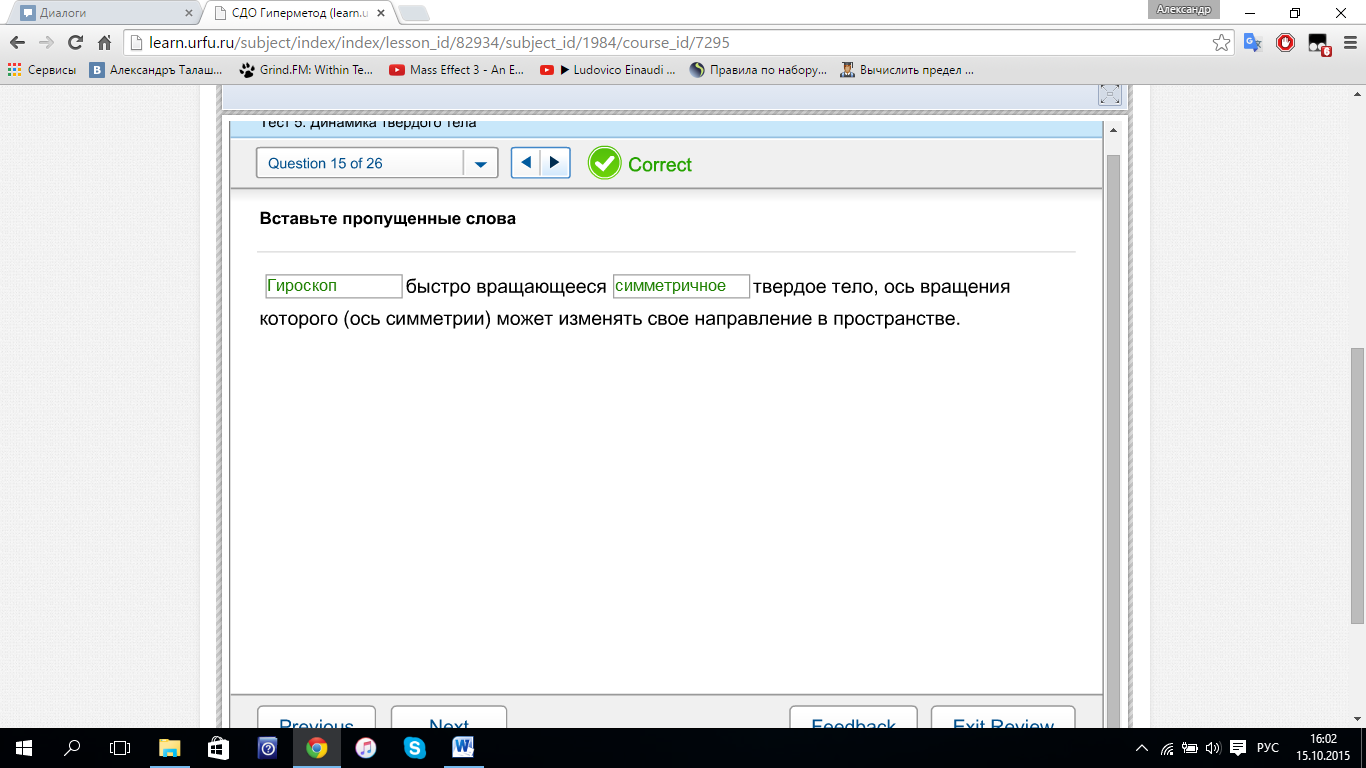ГИРОСКОП быстро вращающееся СИММЕТРИЧНОЕ твердое тело, ось вращения которого (ось симметрии) может изменять свое направление в пространстве.Если неподвижная точка гироскопа совпадает с центром масс, то такой гироскоп называется астатическим (УРАВНОВЕШЕННЫМ), в противном случае – ТЯЖЕЛЫМ.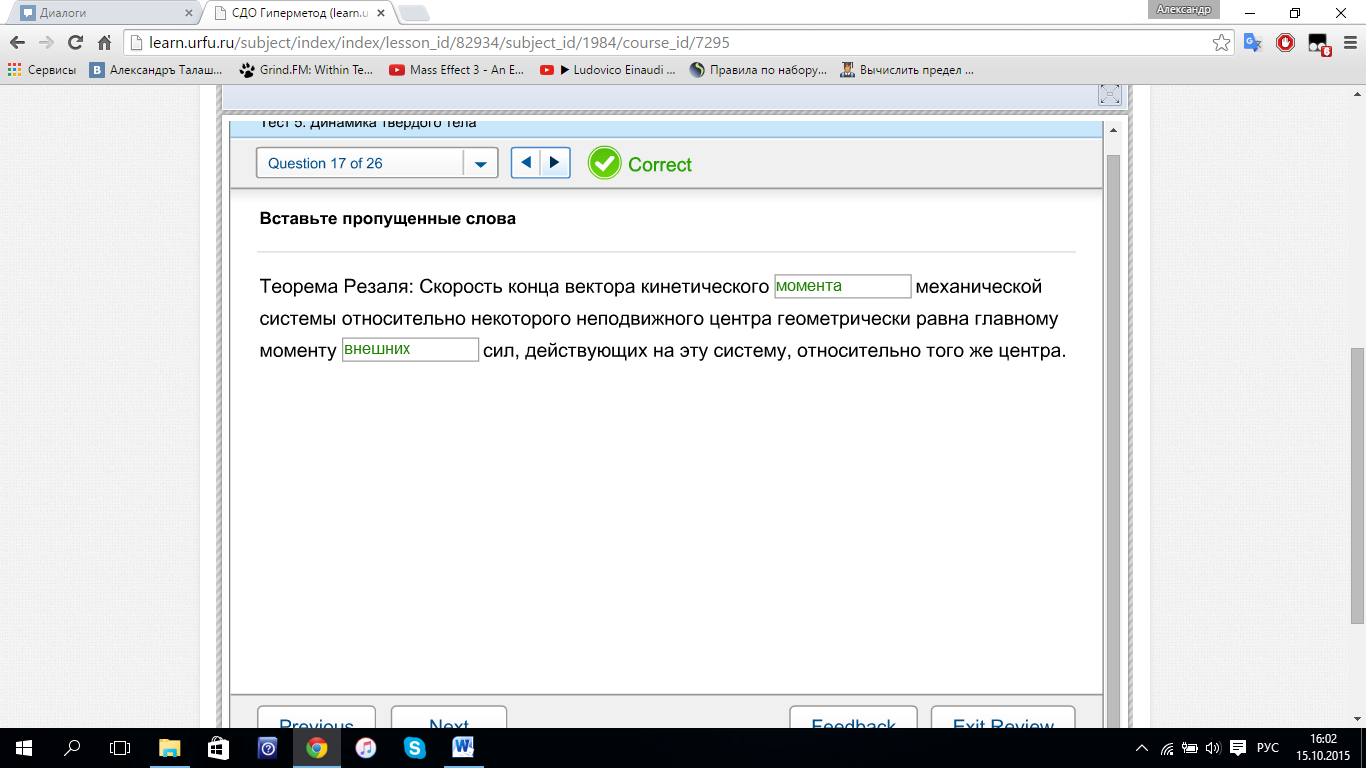Теорема Резаля: Скорость конца вектора кинетического МОМЕНТА механической системы относительно некоторого неподвижного центра геометрически равна главному моменты ВНЕШНИХ сил, действующих на эту систему, относительно того же центра.Первое свойство астатического гироскопа: Ось быстро вращающегося уравновешенного (с ТРЕМЯ степенями свободы) гироскопа устойчиво сохраняет свое направление в ИНЕРЦИАЛЬНОЙ системе отсчета. Удары или толчки могут вызвать вибрацию оси гироскопа, но не отклонение от первоначального положения.

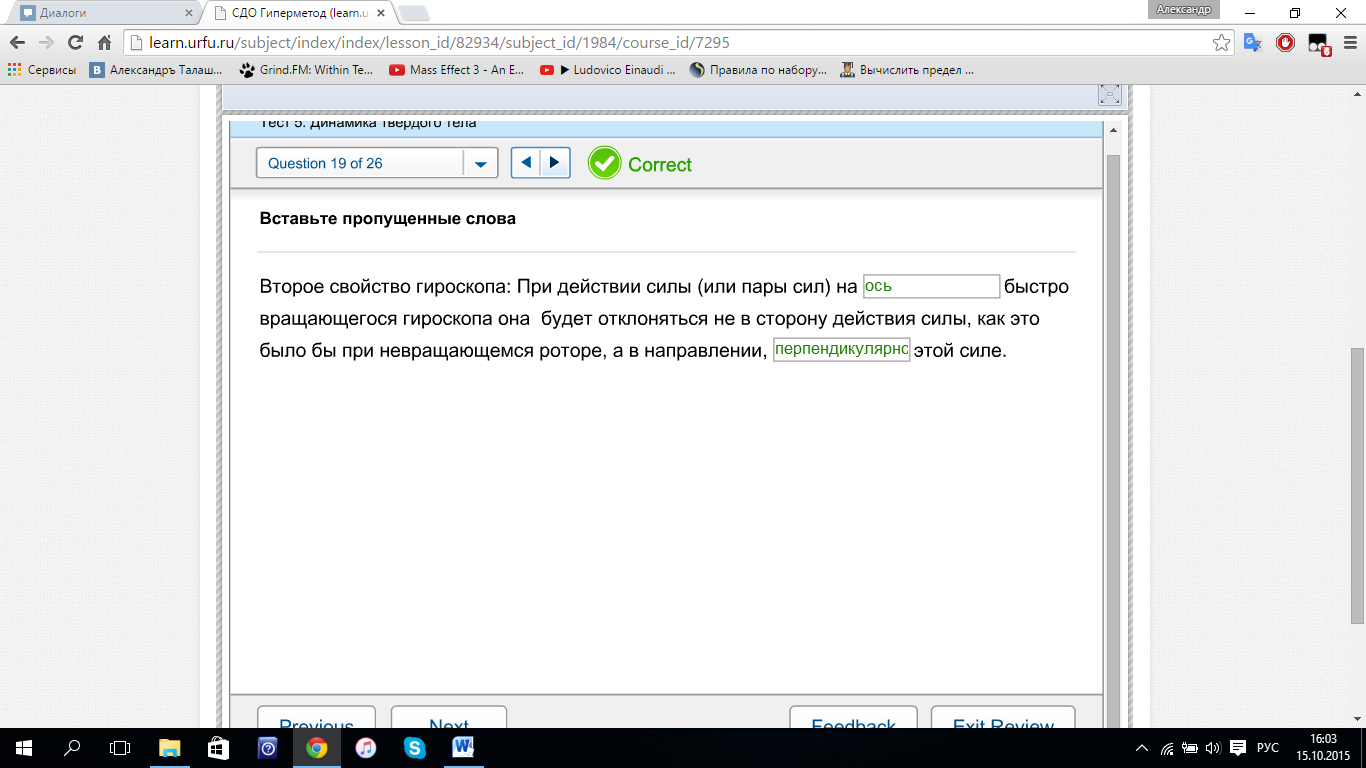
Второе свойство гироскопа: При действии силы(или пары сил) на ось быстро вращающегося гироскопа она будет отклоняться не в сторону действия силы, как это было бы при невращающемся роторе, а в направлении, перпендикулярному этой силе

Это равенство выражает закон прецессии ( верно, где синус)

Это равенство выражает закон прецессии ( верно, где синус)

Регулярная прецессия – движение гироскопа с постоянными угловыми скоростями собственного вращения, прецессии и постоянным углом нутации. В этом случае поверхность, описываемая осью симметрии гироскопа, является круговым конусом

Гироскопические реакции – это силы действующие на ось гироскопа при его принудительном повороте

Момент гироскопических реакций определяется выражением( где синус – правильно)

Момент гироскопических реакций определяется выражением( где синус – правильно)

Правило Жуковского: Если гироскопу сообщают вынужденное прецессионное движение, то возникает гироскопическая пара сил давления на подшипники, стремящаяся кратчайшим путем установить ось гироскопа параллельно оси прецессии так, чтобы векторы угловых скоростей собственного вращения и прецессии совпадали

Силой инерции материальной точки называется сила, равная по модулю произведению массы точки на ее ускорение и направленная в сторону противоположной ускорению. Реально эта сила не приложена к мат.точке, а есть равнодействующая сил, с которыми данная точка действует на взаимодействующие с ней тела.

Принцип Д’Алмабера для материальной точки: если в фиксированный момент движения, кроме действующих на точку сил, добавить силу инерции, то система будет уравновешенной.

Принцип Д’Алмабера для механической системы: если в фиксированный момент времени к каждой точке механической точки, кроме действующих сил, добавить силы инерции, то система сил будет уравновешенной.

Уравнения, получаемы с помощью принципа, по форме совпадают с уравнениями равновесия статики. В общем случае они позволяют получить шесть скалярных равенств( равенства нулю сумм проекций сил, включая силы инерции, на каждую из координатных осей и равенства нулю сумм моментов сил относительно координатных осей). Метод решения задач по динамике, основанный на принципе Д’Алмабера, носит название метода кинетостатики.

Соответствия

Формулы для нахождения главного вектора сил инерции и главного момента сил инерции

При движении несвободного твердого тела реакции связей, действующих на это тело, складываются из статических и добавочных динамических составляющих.

Динамические реакции подшипников при вращении тв. тела

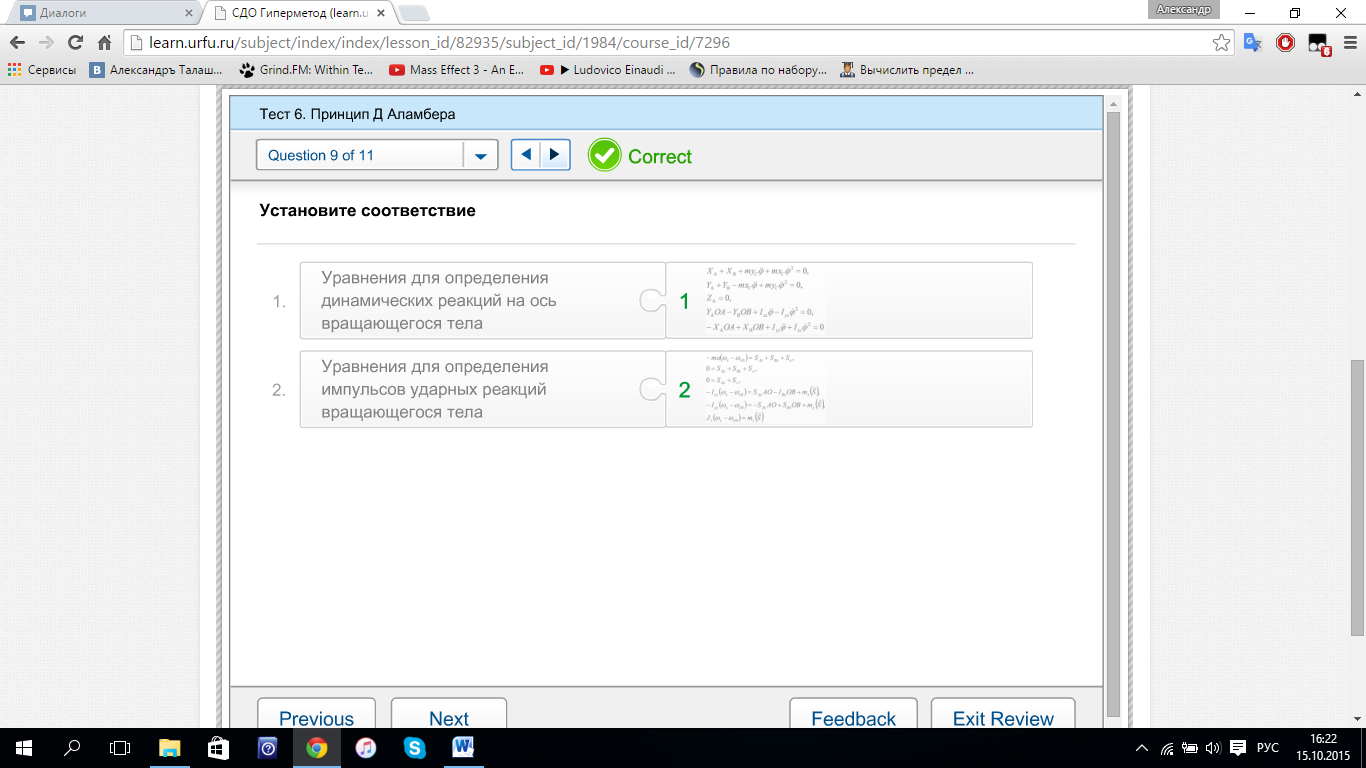
Динамическая реакция на ось вращ. тела и импульсы ударных реакций вращ.тела.

Для того, что бы при вращении тела вокруг неподвижной оси не возникли динамические реакции, необходимо и достаточно, что бы ось вращения являлась главной центральной осью инерции.

Ось вращения всегда можно сделать главной центральной осью инерции, добавляя две точечные массы.

Взаимодействие, при котором за малый промежуток времени скорости точек механической системы изменяются на конечную величину, называется УДАРОМ. Силы, возникающие при таком взаимодействии, называются УДАРНЫМИ.

В теории удара принимают следующие основные допущения:

1. СКОРОСТИ точек изменяются почти мгновенно на конечную величину

2. Импульсами ударных сил пренебрегают

3. Точки системы за время удара не ПЕРЕМЕЩАЮТСЯ

Основное уравнение теории удара: Изменение КОЛИЧЕСТВА движения материальной точки за время удара равно сумме ударных ИМПУЛЬСОВ, действующих на систему

Основное уравнение теории удара

Теорема: Изменение КОЛИЧЕСТВА движения механической системы за время удара равно сумме ВНЕШНИХ ударных импульсов, действующих на точки системы

При действии на механическую систему лишь ВНУТРЕННИХ ударных импульсов КОЛИЧЕСТВО движения системы не изменяется

Теорема: Изменение кинетического МОМЕНТА механической системы относительно любого неподвижного центра за время удара равно сумме МОМЕНТОВ всех внешних ударных импульсов, приложенных к точкам системы, относительно этого же центра

ВНУТРЕННИЕ ударные импульсы не влияют на изменение кинетического МОМЕНТА системы

Теорема: Изменение кинетического МОМЕНТА механической системы относительно неподвижной оси за время УДАРА равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно той же оси

Теорема об изменении количества движения при ударе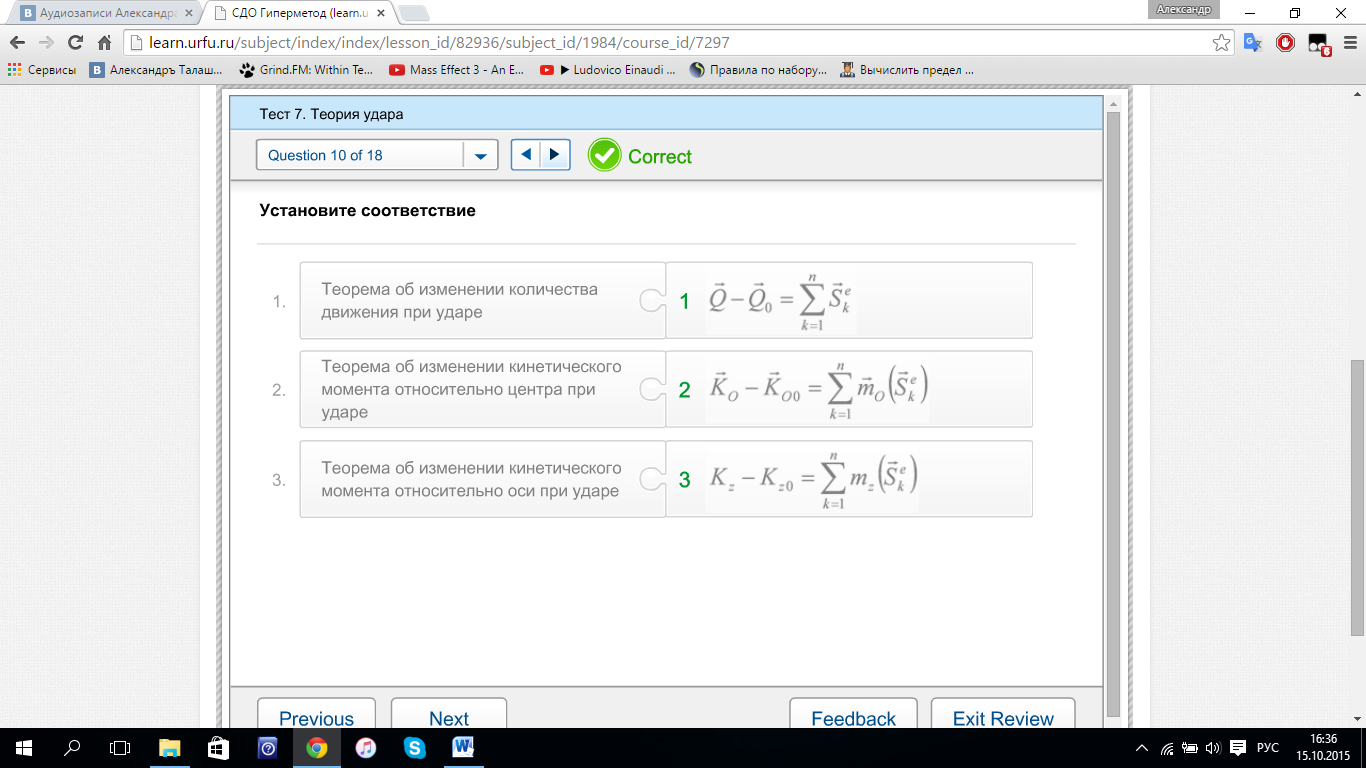

Величина, равная отношению скорости шара малого радиуса после удара к его плоскости до удара, при свободном падении шара на неподвижную плиту, называется коэффициентом восстановления

Коэффициент восстановление при ударе шара

Прямой удар точки о неподвижную плоскость

Теорема Карно: При неупругом ударе в механической системе потеря КИНЕТИЧЕСКОЙ энергии равна кинетической энергии данной системы , если бы она двигалась с ПОТЕРЯННЫМИ скоростями

При действии ударного импульса на вращающееся тело угловая скорость изменяется на величину, равную отношению момента этого импульса относительно оси вращения к моменту ИНЕРЦИИ тела относительно той же оси

Импульсы ударных реакции определяются из уравнения

ЦЕНТР удара это точка вращающегося тела, при действии на которую ударного ИМУЛЬСА, не возникают ударные реакции

Условия:

1. Центр удара лежит в плоскости, проходящей через центр МАСС и ось вращения, на расстоянии равном отношению момента инерции тела относительно оси вращения к произведению массы тела на расстояние от оси вращения до центра масс

2. Ударный импульс направлен ПЕРПЕНДИКУЛЯРНО этой плоскости

3. Ось вращения является ГЛАВНОЙ для точки её пересечения с плоскостью действия ударного импульса