
ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА 7 вариант
.docxМинистерство образования и науки Российской Федерации
ФГАОУ ВПО «Уральский федеральный университет
имени первого Президента России Б.Н.Ельцина»
кафедра теоретической механики
КУРСОВАЯ РАБОТА
по теоретической механике
«ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
Вариант 2210054
Студент Вахтер Р.В.
Группа М-221005
Преподаватель Штернзон В.А.
Комиссия:
Дата _______________
Оценка ______________
__________________(Ф.И.О.)
__________________(Ф.И.О.)
Екатеринбург
2013
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина »
Кафедра теоретической механики
«УТВЕРЖДАЮ»
Зав. кафедрой __________________
«______» _______________ 2013 г.
Задание № 22000011
на курсовую работу
Студент группы ___ М-221005_____специальность/направление___автосервис_________________________
Фамилия Вахтер Имя Роман Отчество Владимирович
Руководитель работы___ Штернзон В.А._____
Срок выполнения с _______ дата выдачи задания________ по ________15.12.2013 г.______
1.Тема курсовой работы: «ДИНАМИКА КУЛИСНОГО МЕХАНИЗМА»
2.Содержание работы (какие графические задания и расчёты должны быть выполнены): выполнение этапов работы в соответствии с методическими указаниями.
3.Особые дополнительные сведения: еженедельные консультации согласно расписанию.
4. План выполнения курсовой работы
|
Наименование элементов работы |
Сроки |
Примечания |
Отметка о выполнении |
|
I этап |
|
|
|
|
II этап |
|
|
|
|
III этап |
|
|
|
|
IV этап |
|
|
|
|
V этап |
|
|
|
|
Защита |
|
|
|
5.Курсовая работа закончена _______________________________________________________
6.Предварительная оценка работы ______________________________________________________
Руководитель _____________________
Вариант 22100054
Динамика кулисного механизма
Кулисный механизм
(рис. 1), состоящий из маховика 1, кулисы
2 и катка 3, расположен в горизонтальной
плоскости и приводится в движение из
состояния покоя вращающим моментом
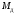 ,
создаваемым электродвигателем. Заданы
массы звеньев механизма; величина
вращающего момента; радиус инерции
катка и радиусы его ступеней; радиус
маховика, представляющего собой сплошной
однородный цилиндр, R1
= 0,36 м; OA =
0,24 м. (табл. 1).
,
создаваемым электродвигателем. Заданы
массы звеньев механизма; величина
вращающего момента; радиус инерции
катка и радиусы его ступеней; радиус
маховика, представляющего собой сплошной
однородный цилиндр, R1
= 0,36 м; OA =
0,24 м. (табл. 1).
Определить:
-
Угловую скорость маховика при его повороте на угол
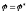 .
. -
Угловое ускорение маховика при его повороте на угол
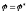 .
.
-
Силу, приводящую в движение кулису в положении механизма, когда
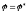 и реакцию подшипника
на оси маховика.
и реакцию подшипника
на оси маховика. -
Силу, приложенную в центре катка и уравновешивающую механизм в положении, когда
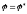 .
.
Записать дифференциальное уравнение движение механизма, используя уравнение Лагранжа второго рода и уравнение движения машины.
Подготовить презентацию к защите курсовой работы, например, в Pоwer Point.
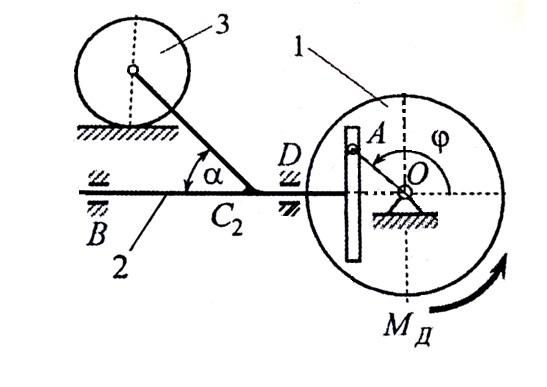
Рис. 1
Таблица 1.
|
|
|
|
|
|
|
|
|
70 |
10 |
12 |
23 |
0,1 |
0,36 |
3π/4 |
Этап I. Кинематический анализ механизма.
1.1. Определение кинематических характеристик
Механизм состоит
из трех звеньев. Ведущим является
маховик 1,
к которому приложен вращающий момент
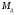 со стороны электродвигателя. От маховика
посредством кулисы 2
движение
передается ведомому звену 3
– катку. Маховик совершает вращательное
движение, кулиса – поступательное,
каток – плоское. Начало координат
помещаем в точку
со стороны электродвигателя. От маховика
посредством кулисы 2
движение
передается ведомому звену 3
– катку. Маховик совершает вращательное
движение, кулиса – поступательное,
каток – плоское. Начало координат
помещаем в точку
 ,
ось
,
ось
 направляем влево, ось
направляем влево, ось
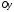 – вверх (рис. 2).
– вверх (рис. 2).
Скорость поступательно
движущейся кулисы находим по теореме
сложения скоростей, рассматривая
движение кулисного камня как сложное.
Переносная скорость т.
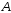 определяет скорость кулисы в ее
поступательном движении.
определяет скорость кулисы в ее
поступательном движении.
Так как
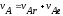 , то
, то
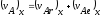 .
.
Откуда
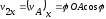 .
.
Скорость центра катка равна скорости кулисы
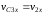 .
.
Откуда
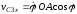 .
.
Угловую скорость катка находим как отношение скорости его центра к расстоянию до мгновенного цента скоростей
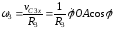 .
.
Ускорение поступательно движущейся кулисы, ускорение центра катка, а также угловое ускорение катка находим дифференцированием, соответственно, скорости поступательно движущейся кулисы, скорости центра катка, а также угловой скорости катка. Откуда
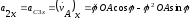 ,
,
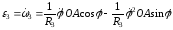 .
.
Укажем векторы
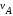 ,
,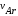 ,
,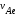 ,
,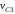 ,
,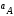 ,
,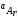 ,
,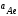 ,
и
,
и
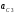 в положении механизма, изображенном в
условии задачи, когда
в положении механизма, изображенном в
условии задачи, когда
 .
Так как динамический расчет еще не
проведен и информация об угловой скорости
маховика и его угловом ускорении
отсутствует, то изображение носит
иллюстративный характер. В данном
положении и кулиса и каток движутся
замедлено. Каток приближается к его
крайнему левому положению.
.
Так как динамический расчет еще не
проведен и информация об угловой скорости
маховика и его угловом ускорении
отсутствует, то изображение носит
иллюстративный характер. В данном
положении и кулиса и каток движутся
замедлено. Каток приближается к его
крайнему левому положению.
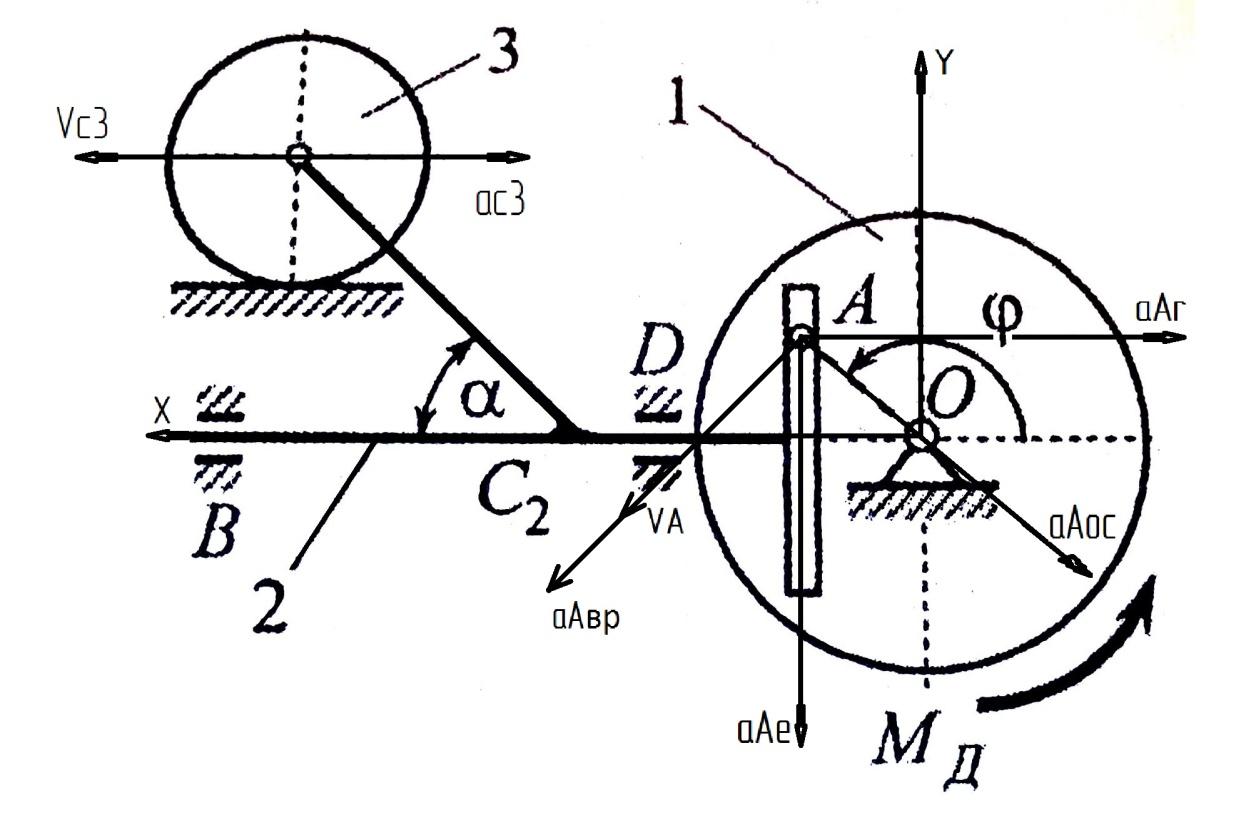
Рис.2
1.2. Запись уравнений геометрических связей
Как и раньше, начало
координат помещаем в точку
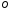 ,
ось
,
ось
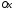 направляем влево, ось
направляем влево, ось
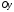 – вверх.
– вверх.
Уравнения связей:
 ,
,
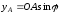 ,
,
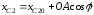 ,
,
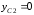 ,
,
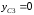 .
.
Интегрируя равенства
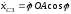 и
и
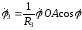
получим
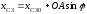 ,
,
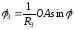 .
.
Этап II. Угловая скорость и угловое ускорение маховика.
2.1. Определение кинетической энергии системы
Кинетическую энергию механизма находим как сумму кинетических энергий его звеньев
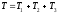 .
.
Кинетическая энергия вращающегося маховика:
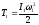 ,
,
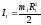 – момент инерции
маховика относительно оси вращения.
– момент инерции
маховика относительно оси вращения.
Кинетическая энергия поступательно движущейся кулисы:
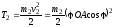 ,
,
Кинетическая энергия катка, совершающего плоское движение:
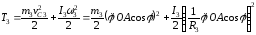 ,
,
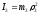 – момент инерции
катка относительно оси, проходящей
через его центр масс.
– момент инерции
катка относительно оси, проходящей
через его центр масс.
Кинетическая энергия системы:
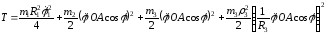 .
.
После тождественных преобразований:
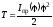 , (1)
, (1)
где
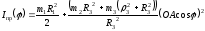 ,
,
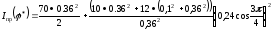
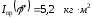 – приведенный к
ведущему звену момент инерции.
– приведенный к
ведущему звену момент инерции.
2.2. Определение производной кинетической энергии по времени
Производную кинетической энергии по времени находим по правилу вычисления производной произведения и производной сложной функции
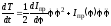 .
(2)
.
(2)
Здесь, 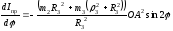
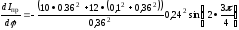
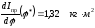 .
.
2.3. Определение элементарной работы, мощности внешних сил. Определение работы внешних сил на конечном перемещении
(механизм в горизонтальной плоскости).
В случае, когда
механизм расположен в горизонтальной
плоскости работу совершает только
вращающий момент
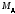 .
Элементарная работа при этом определяется
равенством
.
Элементарная работа при этом определяется
равенством
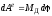 .
.
Мощность
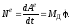 , (3)
, (3)
Работа
при повороте маховика на угол
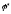
 . (4)
. (4)
2.4. Определение угловой скорости маховика при его повороте
на угол φ*
Для определения угловой скорости маховика применяем теорему об изменении кинетической энергии в конечной форме, полагая, что механизм в начальный момент находился в покое.
 ,
,
 ,
,
 .
.
Подстановка в это равенство найденных выражений (1) и (4) дает
 .
.
Тогда
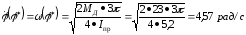 .
.
2.5. Определение углового ускорения маховика при его повороте
на угол φ*
Воспользуемся теоремой об изменении кинетической энергией в дифференциальной форме
 ,
,
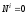 .
.
Подставляя в это уравнение найденные выше значения (2) и (3), находим
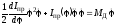 .
.
Откуда
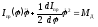 (5)
(5)
и
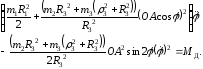
Дифференциальное уравнение второго порядка

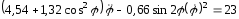
описывает движение кулисного механизма. Оно может быть проинтегрировано только численно, а также использовано для нахождения углового ускорения маховика в произвольном его положении.
Определим угловое
ускорение маховика при угле его поворота
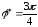 .
.
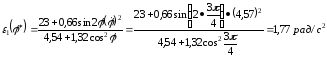 .
.
Этап III. Реакции связей и уравновешивающая сила.
3.1. Определение реакций внешних и внутренних связей в положении φ*
Определим реакцию подшипника на оси маховика и силу, приводящую в движение кулису с помощью принципа д`Аламбера, рассматривая движение маховика отдельно от других тел системы.
Маховик совершает
вращательное движении. Рассмотрим
внешние силы. Помимо пары сил с моментом
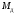 ,
на него действуют
реакция подшипника
,
на него действуют
реакция подшипника
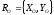 и реакция кулисы
и реакция кулисы
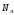 .
Система сил инерции приводится к паре
с моментом
.
Система сил инерции приводится к паре
с моментом
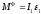 ,
направленным против вращения, т.к. оно
ускоренное (рис.3).
,
направленным против вращения, т.к. оно
ускоренное (рис.3).
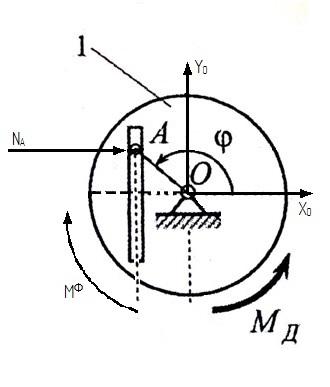
Рис.3
Записывая условие уравновешенности плоской системы внешних сил
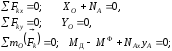
находим
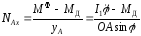
При
угле

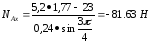 .
.
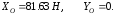
Сила
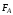 ,
приводящая в движение кулису, по третьему
закону динамики равна реакции кулисы
и направлена в противоположную сторону.
,
приводящая в движение кулису, по третьему
закону динамики равна реакции кулисы
и направлена в противоположную сторону.
3.2. Определение силы уравновешивающей кулисный механизм
Найдем силу,
которую надо приложить к оси катка,
чтобы она уравновешивала действие
момента, создаваемого электродвигателем
в положении маховика
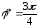 .
.
Для этого воспользуемся принципом виртуальных перемещений
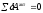
или в аналитической форме, с учетом действующих на систему активных сил:
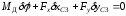 .
.
Используя уравнения связей (см. п.1.2)
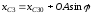 ,
,
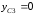 ,
,
находим вариации координат
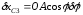 ,
,
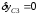 .
.
Подстановка этих соотношений в уравнение принципа виртуальных перемещений дает
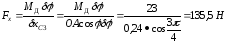 .
.
Любая сила, имеющая
такую проекцию на ось
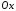 ,
уравновешивает действие вращательного
момента.
,
уравновешивает действие вращательного
момента.

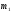 ,
кг
,
кг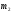 ,
кг
,
кг ,
кг
,
кг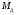 ,
Н·м
,
Н·м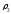 ,
м
,
м ,м
,м ,
рад
,
рад