
- •Классификация трансформаторов и особенности их конструкции.
- •Принцип действия трансформатора. Сущность магнитопровода.
- •Идеализированный трансформатор, его электрические соотношения. Работа на холостом ходу и при нагрузке
- •Электрические соотношения в идеальном трансформаторе Три основных признака идеального трансформатора:
- •Намагничивающий ток и ток холостого хода идеального и реального трансформатора
- •Уравнения и векторные диаграммы реального трансформатора при холостом ходе и нагрузке.
- •В чем состоит необходимость приведения параметров трансформатора? Их физический смысл.
- •Схемы замещения трансформатора
- •Векторные диаграммы «r» и «rc» нагрузки.
- •Векторные диаграммы приведенного трансформатора
- •Упрощение векторной диаграммы
- •Опыт холостого хода трансформатора.
- •Определение параметров намагничивающего контура
- •Опыт короткого замыкания
- •Выражение для определения изменения напряжения трансформатора
- •Определение коэффициента полезного действия
- •Трехфазный трансформатор, маркировка, группы соединения.
- •В чем необходимость параллельной работы трансформатора? Условия включения на параллельную работу. Особенности работы при их нарушении.
- •Переходные процессы в трансформаторах на хх.
-
Схемы замещения трансформатора
Одним из средств изучения работы трансформатора является эквивалентная схема замещения, в которой магнитная связь между обмотками трансформатора замещена электрической связью, а параметры вторичной обмотки приведены к числу витков первичной. Схема (а)
Так как в приведенном трансформаторе k=1, то и –E1=E2. В результате точки a1и a2, b1 и b2 имеют одинаковый потенциал, поэтому на схеме их можно соединить, получив тем самым Т-образную схему замещения трансформатора. (б)
Параметры r1, x1 – активное и индуктивное сопротивления первичной обмотки, соответственно.
r2, x2 – приведенные значения активного и индуктивного сопротивлений вторичной обмотки, соответственно.
Zн – полное сопротивление нагрузки.
Магнитный поток не зависит от нагрузки, поэтому его представляют как индуктивное сопротивление xm, активное сопротивление rm, которое обусловлено магнитными потерями и протекающий через них ток холостого хода I0. Эти параметры определяются в опыте холостого хода трансформатора.
Изменяя Zн на схеме замещения, можно получить любой режим работы трансформатора. Например, при разомкнутой вторичной обмотке Zн= ∞, что соответствует режиму холостого хода трансформатора, а при Zн= 0 – режимукороткого замыкания. При любых других значениях Zн – режим работы под нагрузкой. Режимы работы необходимы для определения параметров схемы замещения.
При практических расчетах, током холостого хода пренебрегают, тогда схема сводится к упрощенной.
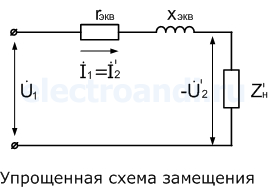
Где rэкв=r1+r2’, xэкв=x1+x2’
-
Векторные диаграммы «r» и «rc» нагрузки.
Воспользовавшись схемой замещения приведенного трансформатора и основными уравнениями напряжений и токов (1.34), построим векторную диаграмму трансформатора, наглядно показывающую соотношения и фазовые сдвиги между токами, ЭДС и напряжениями трансформатора. Векторная диаграмма — графическое выражение основных уравнений приведенного трансформатора (1.34).
Построение
диаграммы (рис. 1.19, а) следует начинать
с вектора максимального
значения основного магнитного потока
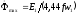 .
.
Вектор тока
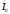 опережает по фазе вектор потока
опережает по фазе вектор потока
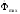 на угол δ, а векторы ЭДС
на угол δ, а векторы ЭДС
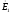 ,
и
,
и
 отстают от этого
вектора на угол 90° [см. (1.6) и (1.7)]. Далее
строим вектор
отстают от этого
вектора на угол 90° [см. (1.6) и (1.7)]. Далее
строим вектор
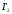 .
Для определения угла
сдвига фаз между
.
Для определения угла
сдвига фаз между
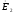 и
и
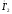 следует знать характер
нагрузки. Предположим, что нагрузка
трансформатора активно-индуктивная.
Тогда вектор
следует знать характер
нагрузки. Предположим, что нагрузка
трансформатора активно-индуктивная.
Тогда вектор
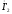 .
отстает по фазе от
.
отстает по фазе от
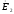 на угол
на угол
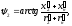 (1.35)
(1.35)
определяемый как характером внешней нагрузки, так и собственными сопротивлениями вторичной обмотки.
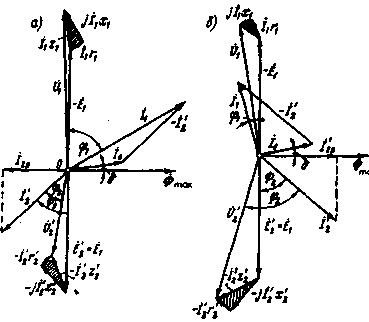
Рис. 1.19. Векторные диаграммы трансформатора при активно-индуктивной (а) и активно-емкостной (б) нагрузках
Для
построения вектора
вторичного напряжения
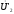 необходимо
из вектора
ЭДС
необходимо
из вектора
ЭДС
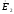 вычесть
векторы падений
напряжения
вычесть
векторы падений
напряжения
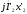 и
и
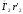 .
С этой
целью из конца вектора
.
С этой
целью из конца вектора
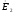 опускаем
перпендикуляр
на направление
вектора тока
опускаем
перпендикуляр
на направление
вектора тока
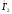 и
откладываем
на нем вектор
и
откладываем
на нем вектор
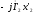 .
Затем проводим
прямую, параллельную
.
Затем проводим
прямую, параллельную
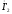 ,
и на ней откладываем
вектор
,
и на ней откладываем
вектор
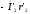 .
Построив
вектор
.
Построив
вектор
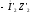 ,
получим
треугольник внутренних
падений напряжения во вторичной цепи.
Затем из точки О
проводим вектор
,
получим
треугольник внутренних
падений напряжения во вторичной цепи.
Затем из точки О
проводим вектор
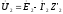 ,
который опережает по
фазе ток
,
который опережает по
фазе ток
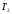 на
угол φ2=arctg(х’н/rн').
на
угол φ2=arctg(х’н/rн').
Вектор
первичного тока строим как векторную
сумму:
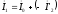 .
Вектор
.
Вектор
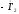 проводим из конца вектора
проводим из конца вектора
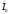 противоположно
вектору
противоположно
вектору
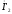 .
Построим вектор
.
Построим вектор
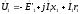 ,
для чего к вектору
,
для чего к вектору
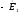 ,
опережающему по фазе
вектор потока
,
опережающему по фазе
вектор потока
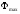 на 90°, прибавляем
векторы внутренних падений напряжения
первичной обмотки:
вектор
на 90°, прибавляем
векторы внутренних падений напряжения
первичной обмотки:
вектор
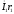 ,
параллельный току
,
параллельный току
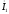 ,
и вектор
,
и вектор
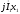 ,
опережающий
вектор тока
,
опережающий
вектор тока
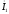 на угол 90°. Соединив точку О
с концом
вектора
на угол 90°. Соединив точку О
с концом
вектора
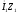 ,
получим
вектор
,
получим
вектор
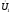 ,
который опережает по фазе вектор тока
,
который опережает по фазе вектор тока
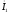 ,
на
угол φ1.
,
на
угол φ1.
Иногда
векторную диаграмму трансформатора
строят с целью определения
ЭДС обмоток. В этом случае заданными
являются параметры вторичной обмотки:
U2,
I2
и соsφ2.
Зная w1/w2,
определяют
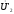 и
и
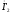 а затем строят векторы этих величин под
фазовым
углом φ2
друг к другу. Вектор ЭДС
а затем строят векторы этих величин под
фазовым
углом φ2
друг к другу. Вектор ЭДС
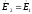 получают
геометрическим
сложением вектора напряжения
получают
геометрическим
сложением вектора напряжения
 с
падениями напряжения
во вторичной обмотке:
с
падениями напряжения
во вторичной обмотке:
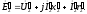
В случае
активно-емкостной нагрузки векторная
диаграмма трансформатора имеет вид,
показанный на рис. 1.19, б. Порядок построения
диаграммы остается прежним, но вид ее
несколько изменяется. Ток
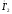 в этом случае опережает
по фазе ЭДС
в этом случае опережает
по фазе ЭДС
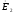 на угол
на угол
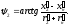 (1.36)
(1.36)
При значительной
емкостной составляющей нагрузки падение
напряжения в емкостной составляющей
сопротивления нагрузки и индуктивное
падение напряжения рассеяния во вторичной
обмотке частично компенсируют друг
друга. В результате напряжение
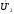 может оказаться
больше, чем ЭДС
может оказаться
больше, чем ЭДС
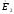 .
Кроме того, реактивная
(опережающая) составляющая вторичного
тока
.
Кроме того, реактивная
(опережающая) составляющая вторичного
тока
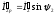 совпадает по фазе с реактивной составляющей
тока х.х.
совпадает по фазе с реактивной составляющей
тока х.х.
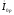 ,
т. е. оказывает на магнитопровод
трансформатора подмагничшающее
действие.
,
т. е. оказывает на магнитопровод
трансформатора подмагничшающее
действие.
Это ведет к
уменьшению первичного тока
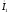 ,
по сравнению с его значением при
активно-индуктивной нагрузке, когда
составляющая
,
по сравнению с его значением при
активно-индуктивной нагрузке, когда
составляющая
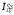 оказывает размагничивающее
влияние (рис. 1.19, а).
оказывает размагничивающее
влияние (рис. 1.19, а).
