Математический анализ

Задание 1

1.

1. Исследовать на непрерывность, построить график функции

2. Исследовать на непрерывность

3. Имеет ли уравнение корень на сегменте [1; 5]?

4. Изобразить график функции, обладающей следующими свойствами:

a);

b) В точкеразрыв 1-го рода и непрерывность слева;

c) В точкеустранимый разрыв;

d).

2.

1. Исследовать на непрерывность, построить график функции

2. Исследовать на непрерывность .

3. Имеет ли уравнение корень на сегменте [1; 6]?

4. Изобразить график функции, обладающей следующими свойствами:

a)

b) В точке разрыв 1-го рода и непрерывность справа;

c) В точкеустранимый разрыв;

d).

Задание 2

1.

1. Вычислить производные:

, ,

, .

2. Вычислить производную параметрически заданной функции

3. Вычислить производную неявной функции

2.

1. Вычислить производные:

, .

2. Вычислить производную параметрически заданной функции

3. Вычислить производную неявной функции

Задание 3

1. Дана функция

1) Исследовать общие свойства функции, найти асимптоты.

2) Исследовать функцию по первой производной.

3) Исследовать функцию по второй производной.

4) Построить эскиз графика.

2. Дана функция

1) Исследовать общие свойства функции, найти асимптоты.

2) Исследовать функцию по первой производной.

3) Исследовать функцию по второй производной.

4) Построить эскиз графика.

Задание 4

1. Вычислите:

1) ;

2) ;

3) ;

4) .

2. Вычислите:

1) ;

2) ;

3) ;

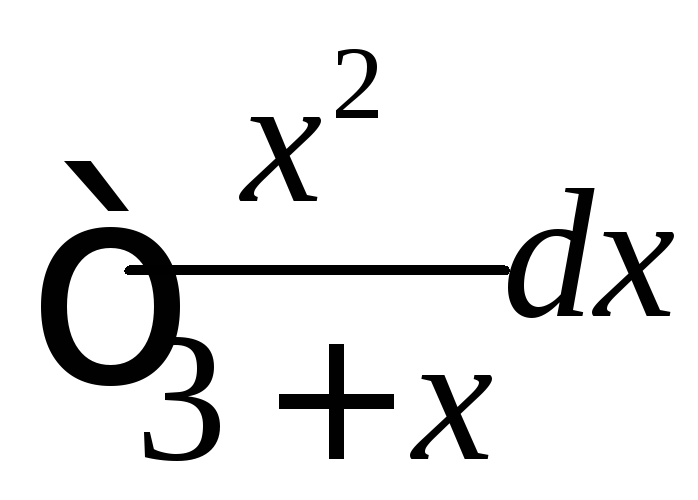4) .

Задание 5

1.

1. Исследовать на сходимость ряд .

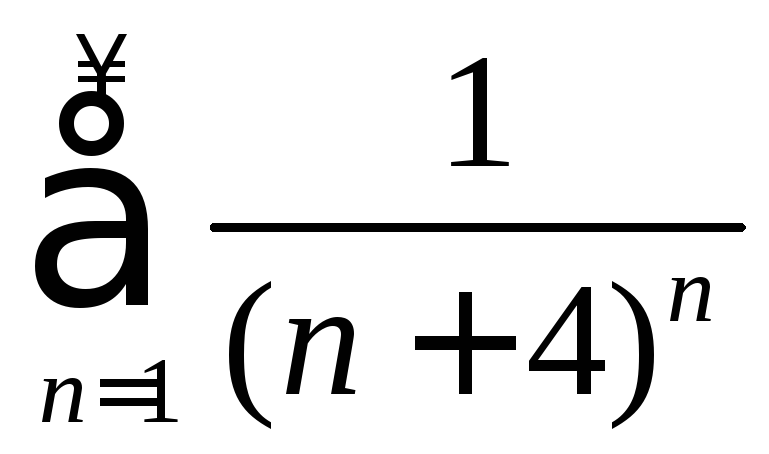2. Исследовать на сходимость ряд .

3. Исследовать на сходимость ряд .

4. Исследовать на абсолютную сходимость ряд .

2.

1. Исследовать на сходимость ряд .

2. Исследовать на сходимость ряд .

3. Исследовать на сходимость ряд .

4. Исследовать на абсолютную сходимость ряд .

Задание 6

1.

1. Найти область сходимости ряда .

2. Найти область сходимости ряда .

3. Найти, используя ряды .

4. Приближенно, с точностью до 0,001 подсчитать .

2.

1. Найти область сходимости ряда .

2. Найти область сходимости ряда .

3. Найти, используя ряды .

4. Приближенно, с точностью до 0,001 подсчитать .

Задание 7

1.

1. Решить уравнение .

2. Доказать, что кривая, в любой точке которой тангенс угла наклона касательной к оси абсцисс пропорционален абсциссе точки касания, есть парабола.

3. Решить уравнение .

4. Решить уравнение .

2.

1. Решить уравнение .

2. Доказать, что кривая, в любой точке которой тангенс угла наклона касательной к оси абсцисс пропорционален абсциссе точки касания, есть парабола.

3. Решить уравнение .

4. Решить уравнение .

Задание 8

1.

1. Решить уравнение .

2. Решить уравнение .

3. Решить уравнение и выделить частное решение по начальным условиям

, .

4. Решить уравнение и выделить частное решение, удовлетворяющее начальным условиям,.

2.

1. Решить уравнение .

2. Решить уравнение .

3. Решить уравнение и выделить частное решение по начальным условиям,.

4. Решить уравнение и выделить частное решение, удовлетворяющее начальным условиям,.

Задание 9

1.

1. Вычислить , , , если , .

2. Найти модуль и аргумент комплексного числа и записать его в тригонометрической форме.

3. Вычислить и изобразить на чертеже .

4. Выяснить, в каких точках плоскости функция является моногенной и вычислить ее производную. Будет ли функция аналитической и где?

2.

1. Вычислить , , , если , .

2. Найти модуль и аргумент комплексного числа и записать его в тригонометрической форме.

3. Вычислить и изобразить на чертеже .

4. Выяснить, в каких точках плоскости функция является моногенной и вычислить ее производную. Будет ли функция аналитической и где?