Примеры вопросов итогового экзамена по математике для бакалавров Алгебра

Тема: Соответствия, отображения и бинарные отношения

1.Даны множества, .

1) Определите типы (всюду определенное, соответствие «на», однозначное, разнозначное) соответствия , если.

2) Найдите композицию отображенийи, еслии

3) Обратимо ли отображение если

4) Докажите, что композиция отображений одного типа является отображением того же типа.

2.Дано множество.

1) Определите свойства (рефлексивность, симметричность, антисимметричность, транзитивность) бинарного отношения

2) Приведите пример наименьшего по включению отношения эквивалентности на множестве

3) Найдите пересечение бинарных отношенийиопределенных на множестве.

4) Докажите свойства классов эквивалентности определенной на множестве.

Тема: Системы линейных уравнений

1.Даны две системы линейных уравнений

(1) 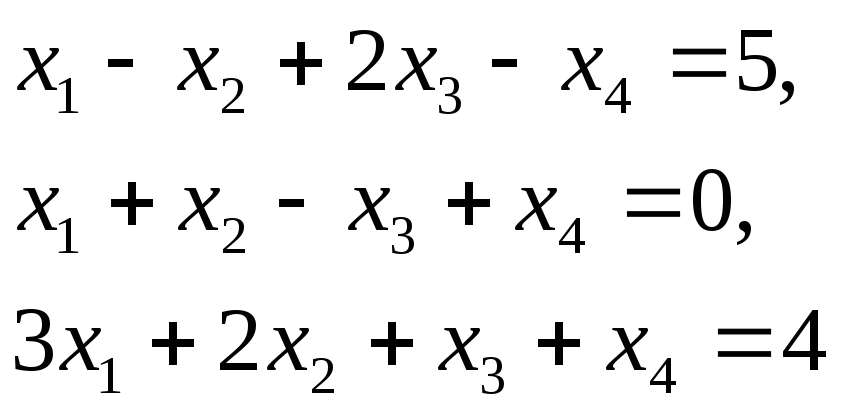и (2)

1) Найдите общее решение системы (1).

2) Равносильны ли системы (1) и (2)?

3) Имеется ли хотя бы одно общее решение у систем (1) и (2)?

4) Докажите, что если система линейных уравнений совместна (разрешима), то ранг матрицы системы равен рангу расширенной матрицы этой системы.

2.Даны две системы линейных уравнений

(1) 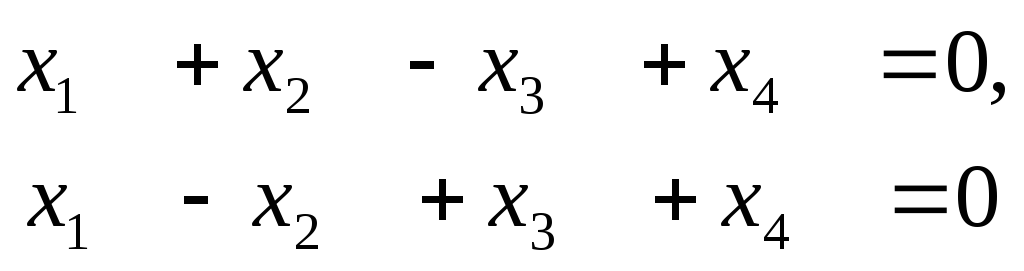и (2)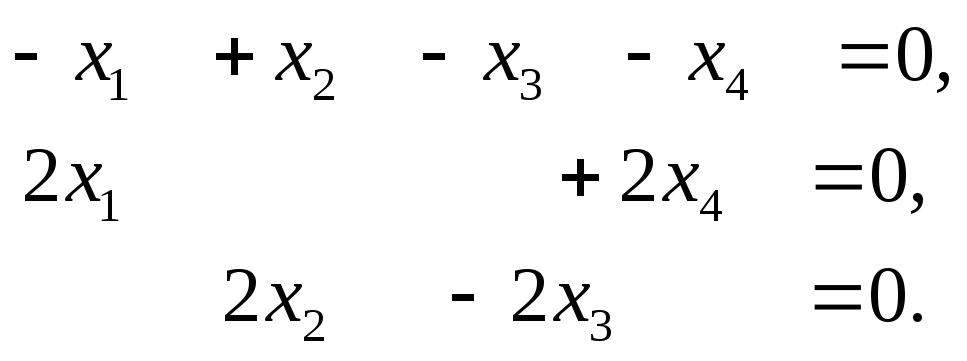

1) Найдите фундаментальную систему решений системы (1).

2) Определите размерность пространства решений системы (2).

3) Равносильны ли системы (1) и (2)?

4) Докажите, что если определитель матрицы квадратной системы линейных уравнений, отличен от нуля, то система имеет единственное решение.

Тема: Матрицы и определители

1. Дано кольцо матриц 4-го порядка с рациональными элементами.

1) Вычислить значение выражения

·+

2) Определите ранг матрицы

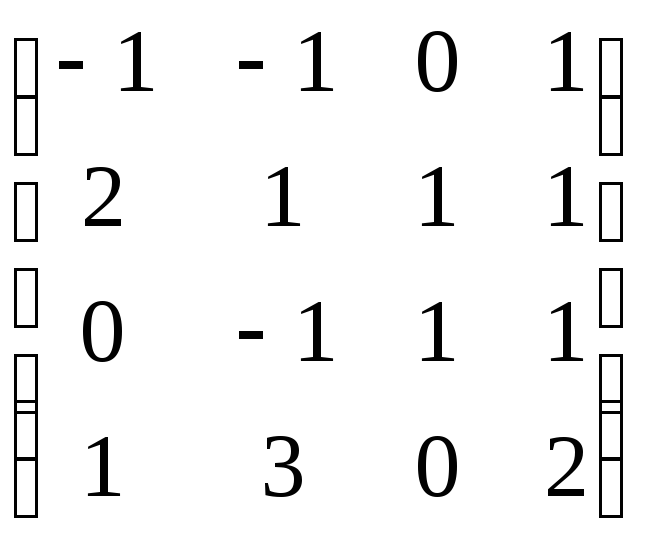
3) Найдите определитель матрицы

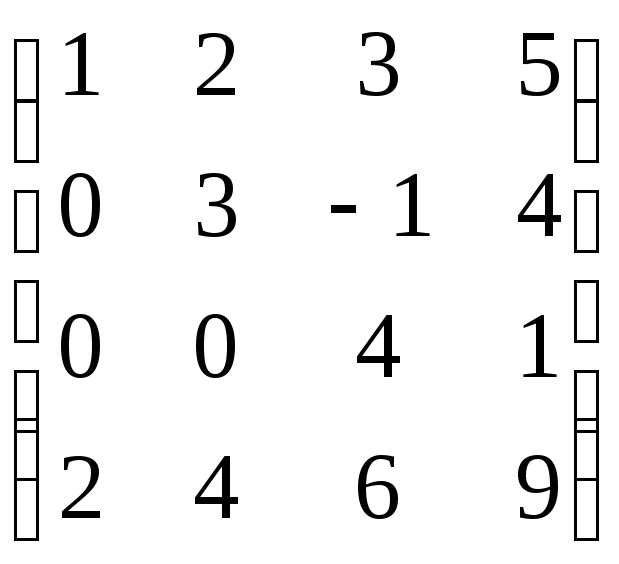
4) Докажите, что если определитель квадратной матрицы отличен от нуля, то она обратима.

2. Дана матрица.

1) Найдите ранг матрицы A =

2) С каким знаком входит произведение элементов в развернутую запись определителя |A| матрицыA?

3) Выпишите максимально возможный набор линейно независимых строк матрицы

4) Докажите, что определитель квадратной матрицы равен сумме произведений элементов некоторой строки этой матрицы на их алгебраические дополнения.

Тема: Комплексные числа

1.Даны два комплексных числаи.

1) Запишите число в алгебраической форме.

2) Запишите число в тригонометрической форме.

3) Изобразите в прямоугольной декартовой системе координат множество всех точек соответствующих комплексным числам , удовлетворяющим условию.

4) Докажите, что для получения тригонометрической формы произведения двух комплексных чисел, заданных в тригонометрической форме, достаточно перемножить их модули а аргументы сложить.

2.Даны два комплексных числаи.

1) Запишите число в алгебраической форме.

2) Найдите все корни уравнения и докажите, что они образуют мультипликативную группу.

3) Изобразите в прямоугольной декартовой системе координат множество всех точек соответствующих комплексным числам , удовлетворяющим условию.

4) Докажите теорему о тригонометрической форме натуральной степени комплексного числа, заданного в тригонометрической форме.

Тема: Группы и кольца

1. Дана группаподстановокn-ой степени.

1) Найдите произведение подстановок

2) Вычислите порядок подстановки f =в группе.

3) Найдите разложение подстановки g= в произведение независимых циклов и определите ее четность.

4) Докажите, что порядок конечной группы делится на порядок подгруппы этой группы.

2.Дано кольцос операциями определенными по правилам:

;.

1) Определите, является ли элемент делителем нуля?

2) Обратим ли элемент (1,2) в этом кольце?

3) Найдите аддитивный порядок элемента (1,1) в этом кольце.

4) Докажите, что если f: – гомоморфизм колец, то подмножествоявляется подкольцом кольцаK.

Тема: Кольцо целых чисел

1.Дано два целых числаa =12342 иb=12495.

1) Найдите каноническое разложение числа a.

2) Найдите остаток от деления числа на 7.

3) Используя алгоритм Евклида, найдите НОД(a,b).

4) Используя аксиоматику Пеано натуральных чисел, докажите теорему о первой форме метода математической индукции.

2.Дано два целых числаa =10164 иb=2904.

1) Решите сравнение .

2) Найдите НОД(a,b), используя алгоритм Евклида.

3) Определите последнюю цифру числа .

4) Докажите, что для любых двух целых чисел a и найдется единственная пара целых чиселqиrтаких, что, где.

Тема: Векторные пространства

1.Даны две системы векторов арифметического векторного пространстванад полемрациональных чисел:

(1) и

(2) .

1) Является ли система (1) линейно независимой?

2) Найдите базис линейной оболочки системы (2).

3) Найдите размерность пространства +.

4) Докажите, что совокупность все векторов пространства у которых последняя координата равна 0, образуют подпространство векторного пространства.

2. Даны система векторов

(1) и векторарифметического векторного пространстванад полемрациональных чисел.

1) Образуют ли векторы системы (1) базис пространства ?

2) Определите координаты вектора в системе (1), если ответ на вопрос 1) положительный.

3) Будет ли система векторов линейно независимой?

4) Докажите, что если ранг матрицы координат некоторой системы векторов, заданных своими координатами в некотором базисе векторного пространства, равен числу этих векторов, то данная система векторов линейно независима.

Тема: Кольцо многочленов одной неизвестной

1.Даны два многочленаис коэффициентами из полярациональных чисел.

1) Найдите все рациональные корни многочлена .

2) Найдите НОД(), используя алгоритм Евклида.

3) Разложите многочлен в произведение неприводимых над полеммногочленов.

4) Докажите, что число всех корней многочлена над полем, считая кратности этих корней, не превосходит степени многочлена.

2.Даны два многочленаис коэффициентами из полярациональных чисел.

1) Разложите многочлен по степеням многочлена.

2) Найдите все рациональные корни многочлена и запишите его разложение в произведение неприводимых над полеммногочленов.

3) Найдите НОД(), используя алгоритм Евклида.

4) Докажите, что для любого многочлена с коэффициентами из целостного кольцаи элементанайдутся единственные многочленс коэффициентами из кольцаитакие, что.

Тема: Кольцо многочленов нескольких неизвестных

1.Дано кольцо многочленов трех неизвестных с коэффициентами из поля.

1) Определите степень многочлена и найдите наивысший член этого многочлена.

2) Найдите представление многочлена в виде многочлена от элементарных симметрических многочленов.

3) Найдите лексикографическое представление многочлена .

4) Докажите, что все симметрические многочлены кольца образуют в нем подкольцо.

2.Дано кольцо многочленовтрех неизвестных с коэффициентами из кольца

1) Найдите наивысший член произведения многочленов .

2) Найдите представление многочлена в виде многочлена от элементарных симметрических многочленов.

3) Найдите лексикографическое представление многочлена .

4) Докажите, что множество всех многочленов из с нулевым свободным коэффициентом образует подкольцо кольца