
11169
.pdfЯкщо результатом масових випробувань є сукупність випадкових подій, які можна охарактеризувати кількісно, то цю кількісну характеристику (лінійний розмір, показник шорсткості, твердість матеріалу тощо) називають випадковою величиною. Наприклад, випадковою величиною може бути діаметр валика як результат механічної обробки партії таких валиків на одному з технологічних переходів.
Випадкові величини позначають великими буквами Х, Y, Z. Їх можливі значення відповідно позначають маленькими буквами x, y, z.
ПРИКЛАД.
Прилад складається з п’яти елементів. Проводили спостереження, які виявили, що за деякий проміжок часу відбулися відмови приладу, які відповідають значенням х1 – х6. Х – випадкова величина число елементів, що відмовили в приладі.
Х: |
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
0 |
1 |
2 |
3 |
4 |
5 |
||
|
х1 = 0 – жоден з елементів приладу не відмовив; х2 = 1 – один з елементів приладу відмовив;
…
Розрізняють дискретні і безперервні (або неперервні) випадкові величини. Дискретна випадкова величина може набувати лише певних, зазвичай
цілочисельних значень. Наприклад, кількість бракованих деталей у партії може бути тільки цілим додатнім числом. Дискретний опис полягає у тому, що вказують всі можливі значення даної величини (наприклад, 7 кольорів звичайного спектра) і для кожного з них вказують ймовірність або частоту спостережень саме цього значення за нескінченно великої кількості всіх спостережень.
Неперервна випадкова величина може набувати будь-яких кількісних значень з безперервного ряду її можливих значень у межах певного інтервалу. Наприклад, розміри деталей, що утворюються як результат механічної обробки, є безперервними випадковими величинами.
Під час випробувань деяка випадкова подія може відбуватися декілька разів. Нехай, наприклад, під час проведених n випробувань подія А відбулася m разів. Число m має назву частоти події. Відношення частоти події m до загальної кількості випробувань n називають імовірністю Р події А.
|
|
P |
m |
. |
|
|
(1.1) |
||
|
|
|
|
|
|||||
|
|
|
|
n |
|
|
|
|
|
Функція розподілу F(x) – це зростаюча функція, значення якої лежать в |
|||||||||
інтервалі [0, 1]. |
|
|
|
|
|
|
|
|
|
Нехай Х – дискретна випадкова величина, тоді маємо ряд розподілу у |
|||||||||
вигляді таблиці: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
випадкова величина Х |
|
х1 |
х2 |
… |
хn |
|
||
|
імовірність появи події Р |
|
Р1 |
Р2 |
… |
Рn |
|
||
|
|
46 |
|
|
|
|
|
|
|
Для побудови графіка функції розподілу маємо:
|
|
P(x x ) 0; |
|
|||
|
|
|
|
1 |
|
|
|
|
|
x x2 ) P1 ; |
|||
|
|
P(x1 |
|
|||
F |
* |
|
|
x x3 ) P1 P2 ; |
||
|
(x) P(x2 |
|||||
|
|
... |
|
|
|
|
|
|
|
5) |
i |
1. |
|
|
|
|
||||
|
|
P(x |
P |
|||
ПРИКЛАД.
Є вибірка 2; 10; 3; 2; 10; 6; 10; 2; 10; 6. Необхідно скласти таблицю і побудувати графік функції розподілу за таблицею.
|
Х |
|
|
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
х2 |
|
|
|
х3 |
|
|
|
х4 |
|
|
випадкова величина |
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
6 |
|
|
10 |
||||||
|
m |
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
m2 |
|
|
m3 |
|
|
m4 |
|||||
|
частота появи події |
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
2 |
|
|
4 |
||||||
|
Р |
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
p2 |
|
|
p3 |
|
|
p4 |
||||
|
імовірність появи події |
|
|
|
3 |
|
=0,3 |
|
1 |
=0,1 |
|
2 |
|
=0,2 |
|
4 |
|
=0,4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
10 |
10 |
10 |
10 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
P1 |
|
m1 |
|
|
|
3 |
0,3. |
pi = 1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
mi |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0, |
x 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0,3(P1 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F * (x) |
0,4 (P P ), |
3 x 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 (P P P ), |
6 x 10; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1(P P |
P |
P ), |
x 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
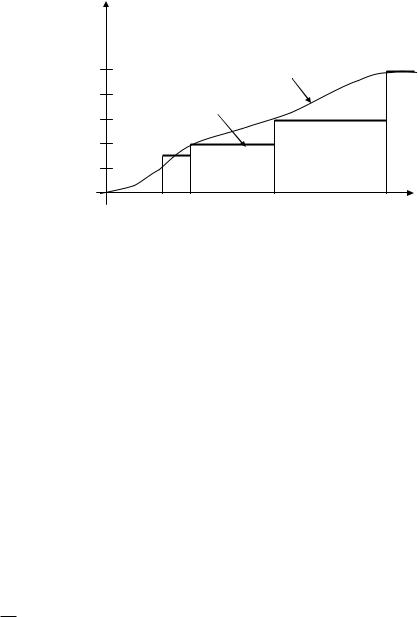
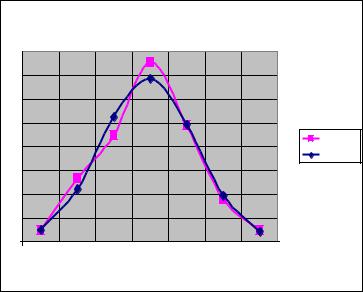
Будуємо графіки емпіричної F*(x) та теоретичної F(x) функцій розподілу – рис.1.11.
Сукупність значень випадкової величини, отриманих під час масових випробувань, розташованих у зростаючому порядку із зазначенням їх імовірності або частоти, називають розподілом випадкової величини.
Статистична сукупність – група предметів, об’єднаних деякою спільною ознакою або властивістю кількісного чи якісного характеру. Наприклад, партію деталей, оброблену зі сталими технологічними умовами на певній операції, можна розглядати як статистичну сукупність. Спільною ознакою може слугувати досліджуваний розмір поверхні або розмір між поверхнями.
Генеральна сукупність – вся множина об’єктів, які підлягають контролю та дослідженню. Для обстеження великих сукупностей використовують вибірки з них.
47
Вибірка – частина об’єктів сукупності, відібраних із неї для отримання інформації про всю сукупність. Кількість об’єктів вибірки називається об’ємом вибірки.
F(x)
F*(x)
1 |
F(x) |
|
|
0,8 |
F*(x) |
0,6 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||
|
|||||||||||||||||
Рисунок 1.16. Графіки емпіричної F*(x) та теоретичної F(x) функцій розподілу
Для того, щоб за даними аналізу вибірки можна було робити висновки про певну ознаку генеральної сукупності, необхідно, щоб об’єкти вибірки правильно її представляли, тобто вибірка має бути репрезентативною.
Під час статистичних досліджень технологічних переходів механічної обробки для забезпечення репрезентативності вибірки оброблених заготовок повинні виконуватись такі умови:
-усі заготовки мають оброблятися безперервно, на одному верстаті, одним інструментом, з однаковими режимами різання;
-верстат має працювати з приблизно однаковими зупинками для встановлення й знімання заготовок, без тривалих перерв;
-усі заготовки мають бути виготовлені з одного й того самого матеріалу;
-під час обробляння заготовок вибірки різальний інструмент не повинен зніматися, переточуватися, правитися й настроюватися.
Усі заготовки вибірки після механічної обробки вимірюються за допомогою універсальних вимірювальних інструментів з ціною поділки, яка не
перевищує 10Т , де T – допуск вимірюваного розміру.
Методика проведення статистичного аналізу вимірювань
За даними проведених вимірювань складають таблицю значень випадкової величини Х.
Якщо вибірка значна, то від точеної оцінки переходять до інтервальної оцінки. Для цього всі значення емпіричного розподілу групують, тобто визначають декілька груп із межами, які повністю перекривають все поле розсіювання δе випадкової величини від мінімального Xmin до максимального Xmax значень всієї сукупності:
e X max X min |
(1.2) |
48
Залежно від вибірки (кількості проведених вимірювань n) визначають, на
скільки інтервалів – груп можна поділити всю емпіричну вибірку. |
|
Кількість груп визначають за формулою Стерджеса: |
|
k = 2 + E (3,322 log n), |
(1.3) |
де n – кількість випробувань;
Е – ціла частина від процедури множення в дужках. Далі треба визначити ширину інтервалу .
Ширина кожного інтервалу залежить від діапазону варіації ознаки Х – е та обґрунтованого числа груп (інтервалів) k (1.3):
= |
X max X min |
. |
(1.4) |
|
|||
|
k |
|
|
Маємо всю сукупність значень випадкової величини та k інтервалів.
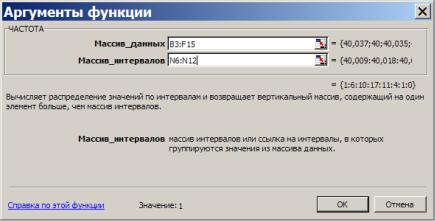
Визначаємося із частотою потрапляння випадкової величини в наперед задані інтервали. Для цього в табличному процесорі треба скористатися із стандартної вбудованої статистичної функції ЧАСТОТА. Процедура визначення наступна. Треба виділити вільний стовпчик поряд із визначеними межами інтервалів (кількість рядків на одиницю більша, ніж кількість інтервалів) та викликати цю функцію. Далі в діалоговому віконці як масив даних визначити весь діапазон випадкової величини, в віконці масив інтервалів – верхні межі інтервалів, що розглядають. У діалоговому вікні натиснути ОК, а далі послідовно натиснути клавіші: F2 , потім натиснути комбінацію клавіш CTRL+Shift+Enter. Стовпчик заповниться значеннями частот, в останньому рядку має бути нуль. Сума всіх значень отриманих частот має дорівнювати кількості значень випадкової величини Х, тобто n.
Рисунок 1.17. Діалогове вікно для визначення статистичної функції Частота
У подальшому, потрібно визначитися із середнім значенням випадкової величини Х, тобто визначити математичне очікування випадкової величини Х. Для цього визначимо спочатку середнє значення (розмір) випадкової величини у кожному інтервалі – Хсері.
49
Знаходять частості. Частість m визначають як відношення частоти події fі до загальної кількості випробувань, тобто кількості виміряних значень n:
|
mi = fi/n. |
Емпірична щільність ye розподілу випадкової величини Х – це відношення |
|
частості до величини інтервалу: |
|
ye=mi/ і |
(1.5) |
Уформулах (1.4) та (1.5) використовують наступні позначення: fi – частота попадання в i-й інтервал,
n – сума всіх частностей fi;
і – ширина і-го інтервалу.
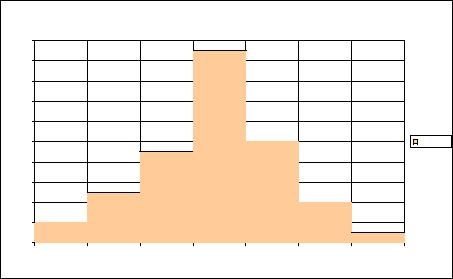
Маючи дані про частоту попадання випадкової величини можна побудувати гістограму значень емпіричних частот – рис. 1.18.
Частота попадання в інтервал
|
|
|
Гістограма частот f |
|
|
|
20 |
|
|
|
|
|
|
18 |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
10 |
|
|
|
|
|
Частота f |
8 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
Номер інтервалу |
|
|
|
Рисунок 1.18. Гістограма емпіричних частот розподілу випадкової величини Х
Визначимо математичне сподівання величини Х за відомою формулою:
|
|
1 |
k |
|
|
X сер |
|
* Xcepi * fi , |
(1.6) |
||
n |
|||||
|
|
i 1 |
|
де n – кількість вимірювань;
Хсері – середній розмір і-го інтервалу; fi – частота і-го інтервалу.
Таким чином, математичне сподівання випадкової величини це таке її значення, до якого прямує середнє значення за достатньо великої кількості спостережень. Це найбільш достовірне значення випадкової величини.
Далі визначаються із мірою розсіювання. Оскільки ми усереднювали допустимі значення випадкової величини Х, то можна усереднити також її відхилення від середнього значення.
50
З огляду на те, що значення різниць (Хсері –Хсер) завжди компенсуватимуть одне одного, потрібно усереднювати не відхилення від середнього, а квадрати цих відхилень.
Величину
k |
|
|
D ( Xcepi |
Xcep)2 fi |
(1.7) |
i 1
прийнято називати дисперсією випадкової величини Х.
Зазначимо, що розмірність дисперсії не збігається із розмірністю випадкової величини і це не дає змогу оцінити величину розброду. Тому частіше замість дисперсії використовують квадратний корінь її значення, тобто середнє квадратичне відхилення або відхилення від середнього значення:
k
( Xcepi Xcep )2 fi
|
i 1 |
. |
(1.8) |
|
|
|
|
|
|
|
|
n |
|
|
Всі проведені математичні операції наведено в таблиці 1.5. Розрахунки проведено в середовищі табличного процесору Excel. Значення середньоквадратичного відхилення СКВ можна визначити, вибравши стандартну функцію «КОРЕНЬ».
Таблиця 1.5 – Розрахунок математичного сподівання та середньоквадратичного відхилення
випадкової величини Х
|
Границі |
Середній |
|
|
Емпірична |
|
|
|
|
|
|
розмір |
|
Частість |
|
|
|
|
|||
|
інтервалу |
Частота f |
щільність |
Додаткові розрахункові вирази |
||||||
|
інтервалу |
m |
||||||||
|
, мм |
|
розподілу ye |
|
|
|
|
|||
№ |
Хсері |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
нижня |
верхня |
Хсері= |
f |
mi=fi/n |
ye=mi/ i |
Xcepi*fi |
Хсері-Хсер |
(Хсері-Хсер)2 |
(Хсері-Хсер)2*fi |
|
|
|
(Хmax+Xmin)/2 |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
40,000 |
40,009 |
40,0045 |
2 |
0,04 |
0,44 |
80,009 |
-0,0263 |
0,00069 |
0,00138 |
2 |
40,009 |
40,018 |
40,0135 |
5 |
0,10 |
1,11 |
200,0675 |
-0,0173 |
0,00030 |
0,00149 |
3 |
40,018 |
40,027 |
40,0225 |
9 |
0,18 |
2,00 |
360,2025 |
-0,0083 |
0,00007 |
0,00062 |
4 |
40,027 |
40,036 |
40,0315 |
19 |
0,38 |
4,22 |
760,5985 |
0,0007 |
0,00000 |
0,00001 |
5 |
40,036 |
40,045 |
40,0405 |
10 |
0,20 |
2,22 |
400,405 |
0,0097 |
0,00009 |
0,00094 |
6 |
40,045 |
40,054 |
40,0495 |
4 |
0,08 |
0,89 |
160,198 |
0,0187 |
0,00035 |
0,00140 |
7 |
40,054 |
40,063 |
40,0585 |
1 |
0,02 |
0,22 |
40,0585 |
0,0277 |
0,00077 |
0,00077 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разом |
50 |
1 |
|
2001,539 |
|
|
0,00661608 |
Xcep (Mатематичне сподівання) = |
|
|
40,03078 |
|
|
1 |
k |
|
|
X сер |
* Xi * fi |
|||
n |
||||
|
i 1 |
|
||
|
|
|||
СКВ 0,01150311
k
( Xcep i Xcep ) 2 f i
i 1
n
Висуваємо гіпотезу стосовно розподілу випадкової величини. Гіпотеза: вхідні параметри Х мають нормальний розподіл. Це найбільш поширений розподіл для рядів варіації. Крива розподілу Гауса використовується як стандарт при порівнянні інших розподілів, а також застосовується при проведенні вибіркового,
51
20
18
16
14
12
10
8

регресійного та факторного статистичних методів дослідження. Диференційна функція розподілу випадкової величини підпорядковується закону нормального розподілу (1.9).
Знайдемо диференційну функцію в кожному з інтервалів:
f ( Xcepi ) |
|
1 |
|
|
( Xcepi Xcep )2 |
(1.9) |
|
|
|
e |
2 2 |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
де Xcepi – середній розмір інтервалу;
Xcep – математичне сподівання випадкової величини Х:
– СКВ – середньоквадратичне відхилення величини Х;
– величина відношення довжини коло до діаметру, = 3,1415;
е– основа натуральних логарифмів, е = 2,7182.
Математична статистика використовує декілька показників, за допомогою яких можна оцінити, наскільки фактичний розподіл узгоджується з нормальним. Такі показники називають критеріями узгодження. Критерії узгодження виступають у вигляді деякої величини, що оцінює явище, що досліджують, з певною ймовірністю.
Для перевірки гіпотези про нормальність розподілу визначимо наступні значення.
Знайдемо диференційну функцію в кожному з інтервалів по формулі (1.9):
|
|
|
1 |
|
|
( Xcepi Xcep )2 |
|
||
f ( Xcepi |
) |
|
|
e |
|
2 2 |
, |
||
|
|
|
|
|
|
||||
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||
або використовуючи стандартну статистичну функцію НОРМРАСП для значень Хсері – середніх значень вибраних інтервалів.
Тут Х – значення Хсер1; Среднее – математичне сподівання;
Стандарное_отклонение – середнє квадратичне відхилення:
ЛОЖЬ – обов’язково писати!!!
Натиснути ОК. Проставити знаки абсолютної адресації біля координат з незмінними параметрами і виконати копіювання цієї формули протягуванням вздовж всього вертикального інтервалу.
52

Отримані значення функції внесемо до розрахункової таблиці (табл.1.5 – продовження).
Для розрахунку значення експоненти рядка 13 доцільно використовувати вбудовану математичну функцію exp – Експонента.
Таблиця 1.5 – Розрахунок математичного сподівання та середньоквадратичного відхилення
випадкової величини Х (продовження)
|
Значення |
|
|
|
|
|
Частоти |
||
безрозмірної |
|
|
|
|
|
||||
|
|
|
|
|
|
||||
змінної, яке |
|
|
|
|
Диференційна |
теоретичної |
|||
|
відповідає |
|
|
|
|
кривої |
|||
|
|
|
|
|
функція |
||||
|
середині |
|
|
|
|
нормального |
|||
|
|
|
|
|
|
||||
|
інтервалу |
|
|
|
|
|
розподілу |
||
|
tj |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
( Xcep i Xcep )2 |
|
|
|
( Xcepi Xcep)2 |
|
f(Xcepi) |
fi ' n * i * f ( Xcepi ) |
|
t j |
e |
2 2 |
|||||||
2 2 |
|
|
|||||||
|
12 |
|
13 |
|
14 |
15 |
|||
|
2,610 |
|
0,074 |
2,551 |
1 |
||||
|
1,128 |
|
0,324 |
11,222 |
5 |
||||
|
0,259 |
|
0,772 |
26,767 |
12 |
||||
|
0,002 |
|
0,998 |
34,614 |
16 |
||||
|
0,357 |
|
0,700 |
24,269 |
11 |
||||
|
1,324 |
|
0,266 |
9,226 |
4 |
||||
|
2,904 |
|
0,055 |
1,902 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
Визначимо частоту теоретичної кривої закону нормального розподілу для кожного з и інтервалів за формулою:
|
fi ' n * i * f ( Xcepi ) |
(1.10) |
де |
n – кількість вимірювань; |
|
I – ширина і-го інтервалу, згідно (1.4); f(Xcepi) – диференційна функція (1.9).
Отримані значення показано в таблиці 1.5 (продовження). Побудуємо графіки емпіричної та теоретичної кривих розподілу випадкової величини Х –
рис.1.17.
Таблиця 1.6 – Додаткові розрахункові вирази для знаходження критерію Пірсона
випадкової величини Х
Додаткові розрахункові вирази
f-f' |
(f-f')2 |
(f-f')2/f' |
|
|
|
16 |
17 |
18 |
|
|
|
1 |
0,7 |
0,632 |
0 |
0,0 |
0,000 |
-3 |
9,3 |
0,770 |
3 |
11,7 |
0,753 |
-1 |
0,8 |
0,078 |
0 |
0,0 |
0,006 |
0 |
0,0 |
0,024 |
53
Згадаємо, що математична статистика використовує показники, за допомогою яких можна оцінити, наскільки фактичний розподіл узгоджується з нормальним. Такі показники називають критеріями узгодження. Критерії узгодження є деякою величиною, що оцінює явище, що досліджують, з певною ймовірністю. Статистика використовує критерії узгодження К. Пірсона ( 2), А.Н. Колмогорова ( ), Б.С. Ястремського (L), В.І. Романовського (R), З. Фішера (Z) та інших. Одними з основних та найбільш поширених є критерії К. Пірсона 2 та Колмагорова .
Англійський вчений Карл Пірсон запропонував критерій – 2( критерій ХІквадрат), статистичну характеристику якого обчислюють за формулою:
2 |
|
( f |
f ')2 |
, |
(1.11) |
|
f ' |
||||
|
|
|
|
|
де f і f’ – відповідно фактичні (емпіричні) та теоретичні частоти.
Критерій узгодження Карла Пірсона дозволяє здійснити перевірку емпіричного та теоретичного (або іншого емпіричного) розподілу однієї ознаки. Цей критерій застосовують у двох випадках:
•для зіставлення емпіричного розподілу ознаки з теоретичним розподілом (нормальним, рівномірним або будь-яким іншим законом);
•для зіставлення двох емпіричних розподілів однієї і тієї ознаки.
Ідея методу - визначення міри розбіжності відповідних частот f і f’. Чим більша ця розбіжність, тим більше значення 2емп (1.11).
Об'єми вибірок мають бути на меншими за 50 значень та необхідна рівність частот:
k
fi
i 1
k
fi '.
i 1
Нульова гіпотеза Н0 ={два розподілу практично не відрізняються між собою}; альтернативна гіпотеза – Н1 ={ розбіжність між розподілами суттєва}.
Наведемо схему застосування критерію Пірсона зіставлення двох емпіричних розподілів на рис.1.19.
|
|
|
|
Перевірити |
|
|
|
|
|
|
|
|
∑fi=∑f’i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Записати частоти fi та |
|
|
|
|
|
|
Розрахувати |
|
f’I двох вибірок по K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(fi-f’i)2/f’i |
|
|
інтервалам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо |
|
|
|
|
|
Знайти значення |
|
|
χ2емп≤Χ2крит |
|
|
|
|
|
∑(fi-f’i)2/f’i=χ2емп |
|
|
приймають гіпотезу Н0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайти по таблиці |
|
|
|
|
|
|
|
|
Χ2крит(α, К-1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.19. Схема застосування критерію Пірсона
54
Залежно від ступенів вільності за спеціальними таблицями або за допомогою вбудованих статистичних функцій табличного процесора визначають імовірність досліджуваного значення 2.
Число ступенів вільності визначають за формулою
к-1, |
(1.12) |
де к – число груп. |
|
Якщо отримане за формулою (1.11) фактичне значення 2емп |
менше |
табличного ( 2емп < 2крит), то це означає, що при прийнятому рівні значущості розходження між фактичними і теоретичними частотами вважаються випадковими, гіпотеза про закон розподілу приймається.
Розраховуємо критерій Пірсона згідно формули (1.11) для перевірки гіпотези про нормальність розподілу отриманих емпіричних значень. Значення фактичних та теоретичних частот наведено в таблиці 1.15. Додаткові розрахункові вирази для розрахунку заносимо в таблицю 1.16. Для даних, розрахованих в таблиці, значення фактичного критерію дорівнюватиме 2емп=2,263. Можна знайти табличне значення цього параметру за умови, що прийнято рівень довіри, що складає 0,95, та число ступенів вільності.
Табличне значення дорівнює 2 крит=9,49.
Тобто виконується умова
( 2емп < 2крит).
Це означає, що рівні значущості розходження між фактичними і теоретичними частотами вважаються випадковими, гіпотеза про закон розподілу приймається.
|
Теоретична та емпірична крива розподілу Х |
|
|||||
40 |
|
|
|
|
|
40 |
|
35 |
|
|
|
|
|
35 |
|
30 |
|
|
|
|
|
30 |
|
25 |
|
|
|
|
|
25 |
|
20 |
|
|
|
|
|
20 |
Емпірична |
|
|
|
|
|
теретична |
||
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
15 |
|
10 |
|
|
|
|
|
10 |
|
5 |
|
|
|
|
|
5 |
|
0 |
|
|
|
|
|
0 |
|
40,005 |
40,014 |
40,023 |
40,032 |
40,041 |
40,050 |
40,059 |
|
|
|
|
Хсері |
|
|
|
|
Рисунок 1.20. Графіки теоретичної та емпіричної функцій розподілу.
Приклад проведених розрахунків з використанням табличного процесора Excel
– розрахункові таблиці, показано на рис.1.21.
55
