laba_1_ilin

ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Красноярский институт железнодорожного транспорта

филиал Федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра : «Системы обеспечения движения поездов»

ЛАБОРАТОРНАЯ РАБОТА

По дисциплине: «Теория передачи сигналов»

Выполнил: студент группы:

СОД.2-12-1

К-12-СОД.2-0273к

Пономарев Владимир Александрович

Проверил:

Ильин Евгений Сергеевич

Красноярск

КрИЖТ ИрГУПС

2015г.

Лабораторная работа №1.

Тема: Спектральный анализ сигналов.

Цель: Исследование формы и спектра гармонических и импульсных сигналов. Формирование знаний и умений анализа сигналов на основе реальных и виртуальных устройств, а также приобретение опыта моделирования различных сигналов и исследования спектральных характеристик при изменении параметров сигналов.

Оборудование: вольтметр, двулучевой осциллограф и ПК в режимах отдельных устройств, а также приборы с программным обеспечением РС Lab2000, работающие совместно с ПК, для успешного использования которых целесообразно обратиться к инструкции и меню Help PC_Lab2000.

а) б)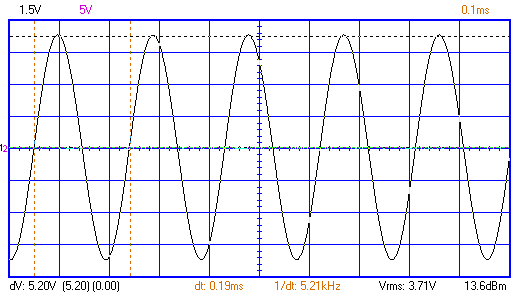

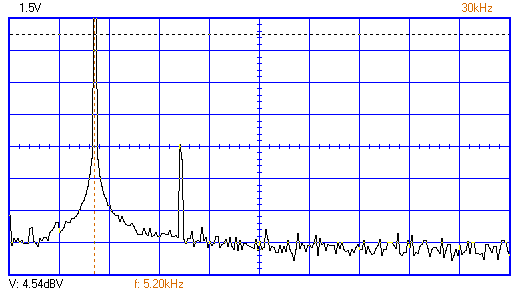
Рисунок 1 – Осциллограмма и спектр гармонического сигнала с частотой 5,2кГц.

S(t)=Acos*(wt+y) A=5.2В

w=2πf=6.28*5.2=32.65.

S(w)=Aπ[δ(w-w₀)=δ(w+w₀)]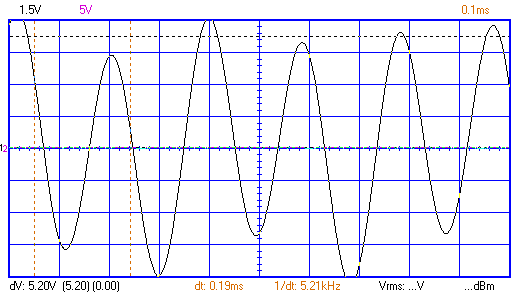

W₀=2πf=6.28*5.2*10³=32656

а)

б)

Рисунок 2 – Осциллограмма и спектр бигармонического сигнала с частотой 5,2кГц.

а)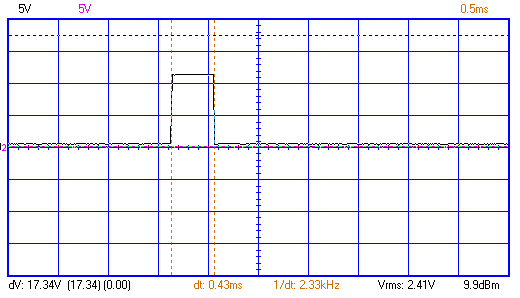

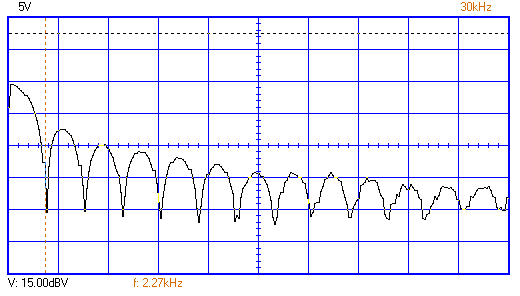
б)

Рисунок 3 – Осциллограмма и спектр импульсного сигнала.

Временное и частотное описание одиночного импульсного сигнала.

Все многообразие сигналов, используемых при передаче информации, можно разделить на две группы: детерминированные и случайные. Первые характеризуются тем, что в любые моменты времени их значения являются известными величинами. Сигналы, значения которых в любые моменты времени заранее неизвестны, называются случайными. Существуют две равноценные формы представления сигналов как функций времени и частоты. Соответственно, любой непрерывный сигнал может быть изображен в виде временной диаграммы и в виде частотной или спектральной диаграммы. Так, временная и спектральная диаграммы гармонического колебания , где 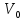- амплитудное, т.е. максимальное значение сигнала, 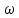0 - угловая частота, , 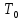- период колебаний, 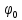- начальная фаза, показаны на рис. 4.

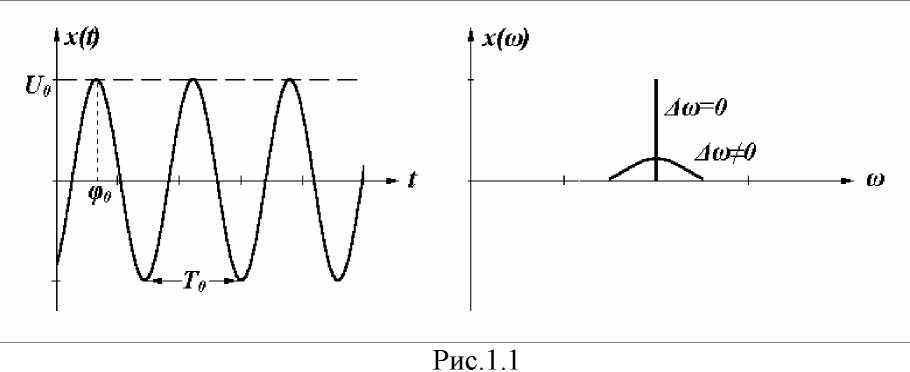
Рисунок 4

И та, и другая формы изображения сигналов равноценны. Каждая из них несет сведения об амплитуде, частоте или периоде колебаний; по ширине спектральной линии или просто по спектру можно судить о продолжительности сигнала Т. Если , т.е. сигнал монохроматичен, в его составе только одна гармоника. Это бывает в том случае, когда продолжительность сигнала равна бесконечности. 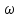Если Т уменьшается, спектр "размывается",, в составе сигнала появляется бесконечно много бесконечно близких к 0 гармонических составляющих, амплитуда каждой из которых бесконечно мала. Реально ни один сигнал не существует бесконечно долго, иначе его энергия была бы равна бесконечности. Поэтому время существования сигнала Т - относительно. Для гармоники частотой 1МГц время существования Т=1мс практически «бесконечно». Заметим, что гармоническое колебание (рис.4) является самым простым колебанием, т.к. оно происходит с минимальной затратой энергии.

Почти всякое колебание в природе происходит по гармоническому закону, по закону синусоидальных или косинусоидальных колебаний. На первой взгляд прямоугольные колебания кажутся даже проще гармонических - постоянное напряжение включается и выключается, однако, при этом происходит, например, перенос заряда из одного потенциального состояния в другое мгновенно, что требует очень больших затрат энергии, поэтому такие колебания являются одними из самых сложных. Спектральное представление сигналов в технике является более удобным, особенно при описании случайных сигналов. Спектральное представление сигналов дает возможность определить, как с допустимыми искажениями по форме пропустить данный сигнал через элементы канала, линии связи, фильтры, усилители и другие устройства, всегда имеющие ограниченную полосу пропускания, которые, как и сигналы, могут быть представлены функциями частоты. Строго говоря, гармонические колебания, как и более сложные периодические колебания, являясь детерминированными, не могут нести информации и, следовательно, не считаются сигналами. Это - модели сигналов, носители информации, на параметры которых может быть нанесена информация.