Типовое (зачётное) задание по теории вероятностей №9, 2012-13 уч. Год

1. Получена партия из восьми изделий одного образца. По данным проверки половины партии три изделия оказались технически исправными, а одно бракованным. Какова вероятность, что при проверке трёх последующих изделий одно из них окажется исправным, а два бракованными, если любое количество бракованных изделий в данной партии равновозможно?

2. Два стрелка поочерёдно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0,4 и 0,5, а вероятность попадания при последующих выстрелах для каждого увеличивается на 0,05. Какова вероятность, что первым произвёл выстрел первый стрелок, если при пятом выстреле произошло попадание в мишень.

3. В каких случаях имеет место равенство ?

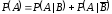4. Какова вероятность того, что при игре в преферанс в прикупе туз треф и валет бубен?

5. На плоскость, разграфлённую параллельными прямыми, отстоящими друг от друга на расстоянии 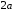наудачу бросают иглу длины 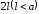. Найти вероятность того, что игла пересечёт какую-нибудь прямую.

Типовое (зачётное) задание по теории вероятностей №10, 2012-13 уч. Год

1. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятности того, что вепрь убит первым, вторым или третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6.

2. Третья часть одной из трёх партий деталей является второсортной, остальные детали первого сорта. Деталь, взятая из одной партии, оказалась первого сорта. Определить вероятность того, что деталь была взята из партии со второсортными деталями. Найти ту же вероятность при условии, что взятая из той же партии вторая деталь оказалась первосортной, если первая деталь после проверки возвращена в партию.

3. В сосуд, содержащий шаров, опущен белый шар. Какова вероятность извлечь из этого сосуда белый шар, если все предположения о первоначальном числе белых шаров равновозможны?

4. Доказать формулу: .

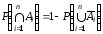5. На отрезке 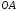длины 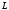числовой прямой наудачу поставлены две точки: и . Найти вероятность того, что из трёх получившихся отрезков можно составить треугольник.

Типовое (зачётное) задание по теории вероятностей №11, 2012-13 уч. Год

1. На отрезок ОА длиной 7см ставят наугад две точки В и С. Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей из точек В и С, а также найти вероятность того, что длина отрезка ВС меньше 4см.

2. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым - 0,8, третьим стрелком - 0,9. Определить вероятность того, что: а) все три стрелка одновременно попадут в цель; б) в цель попадёт хотя бы один стрелок.

3. Партия из 50 изделий подвергается выборочному контролю. Условие негодности всей партии - наличие хотя бы одной бракованной детали среди 5 проверенных. Какова вероятность того, что партия не будет принята, если она содержит 5% бракованных деталей?

4. Три охотника выстрелили по зайцу, который был убит одной пулей. Определить вероятность того, что заяц убит каждым из охотников, если вероятность попадания первым 0,2, вторым - 0,4, а третьим - 0,6.

5. Принимая, что вероятность рождения однополых близнецов в два раза выше, чем разнополых, вероятности рождения близнецов разного пола в любой последовательности одинаковыми, а вероятность рождения мальчика 0,51, а девочки 0,49, определить вероятность рождения второго мальчика, если первым родился мальчик.