§5. Графическое решение задач вида () и ().

Пример 5.1. Найти оптимальное решение игры (), заданной в виде следующей платежной матрицы:

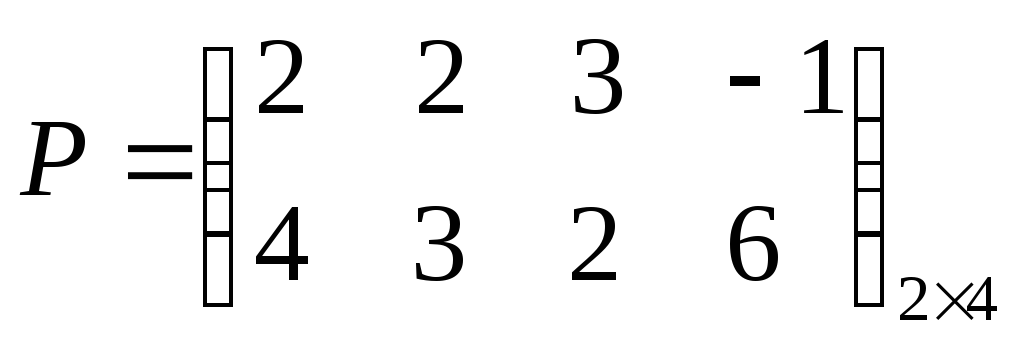
Все расчеты удобно проводить в таблице :

Таблица 5.1

Аi \ Bj	В1	Вг	В3	В4	α i
А1	2	2	3	-1	-1
A2	4	3	2	6	2
β j	4	3	3	6	α =2\ β = 3

На оси абсцисс откладываем отрезок единичной длины (рис.5.1), из концов которых откладываем выигрыши игрока А, соответствующие различным сочетаниям стратегии игроков А и В.

Максимальной оптимальной стратегии игрока А соответствует точка N, лежащая на пересечении прямых В₄В₄, В₂В₂ и В₃В₃, для которых можно записать следующую систему уравнений:

Рис.5.1

Уравнение прямой В₄В₄ ,проходящей через точки (0; -1) и (1;6):

Уравнение прямой В₃В₃ ,проходящей через точки (0; 3) и (1;2):

Уравнение прямой В₂В₂ ,проходящей через точки (0; 2) и (1;3):

Точка пересечения прямых В₂В₂ и В₄В₄ является решением системы:

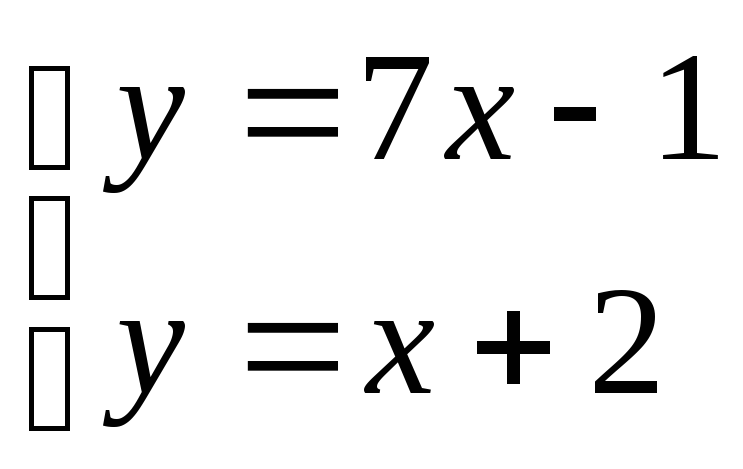
или х = 1/2, у = 5/2 , т.е. N (1/2 ;5/2).

Таким образом, p*₁ =1/2 ,p*₂ =1 - 1/2 = 1/2. Оптимальная стратегия S*_A=(1/2 ;1/2), цена игры ν = 5/2.

Пересечение нескольких прямых говорит о наличии альтернативного плана.

Пример 5.2. Найти оптимальное решение игры (), заданной в виде следующей платежной матрицы:

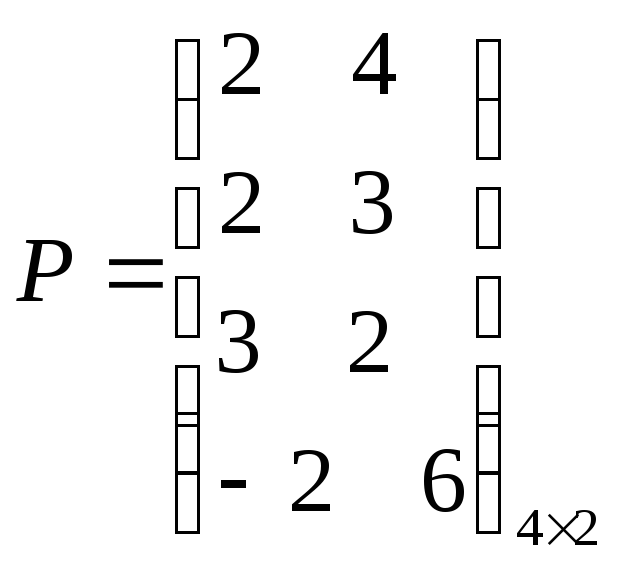
Таблица 5.1

Аi \ Bj	В1	Вг	α i
А1	2	4	2
A2	2	3	2
А3	3	2	2
A4	-2	6	-2
β j	3	6	α =2\ β = 3

Рассмотрим решение с позиции минимаксной стратегии игрока В. На оси абсцисс (рис.5.2) строим отрезок единичной длины, точки которой соответствуют различным стратегиям игрока В. На осях ординат откладываем проигрыши игрока В, соответствующие каждой стратегии игрока А.

Граничная ломаная выделяется сверху, что соответствует минимаксной стратегии игрока В. Точка N на ломаной А₁, А₄ и А₃ соответствует минимаксному проигрышу игрока В при осторожной тактике и определяется на пересечении отрезков А₁А₁, А₃А₃ и А₄А₄.

Уравнение прямой А₁А₁ ,проходящей через точки (0; 2) и (1;4):

Уравнение прямой А₃А₃ ,проходящей через точки (0; 3) и (1;2):

Рис.5.2

Граничная ломаная выделяется сверху, что соответствует минимаксной стратегии игрока В. Точка N на ломаной А₁, А₄ и А₃ соответствует минимаксному проигрышу игрока В при осторожной тактике и определяется на пересечении отрезков А₁А₁, А₃А₃ и А₄А₄.

Уравнение прямой А₄А₄ ,проходящей через точки (0; -2) и (1;6):

Найдем точку пересечения прямой А₁А₁ и А₃А₃:

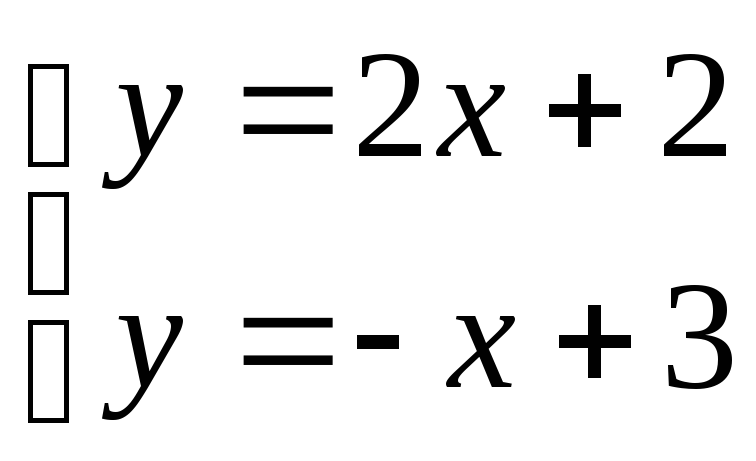
или х = 1/3, у = 8/3 , т.е. N (1/3 ;8/3).

Найдем точку пересечения прямой А₁А₁ и А₃А₃:

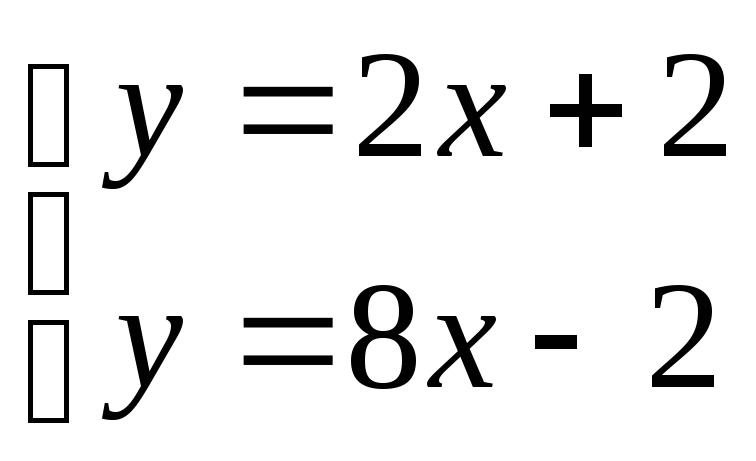
или х = 2/3, у = 10/3 , т.е. N (2/3 ;10/3).

Таким образом, оптимальное решение

,,

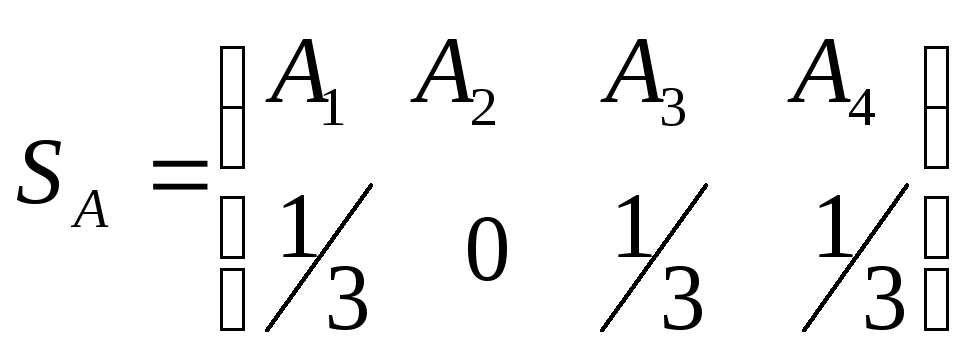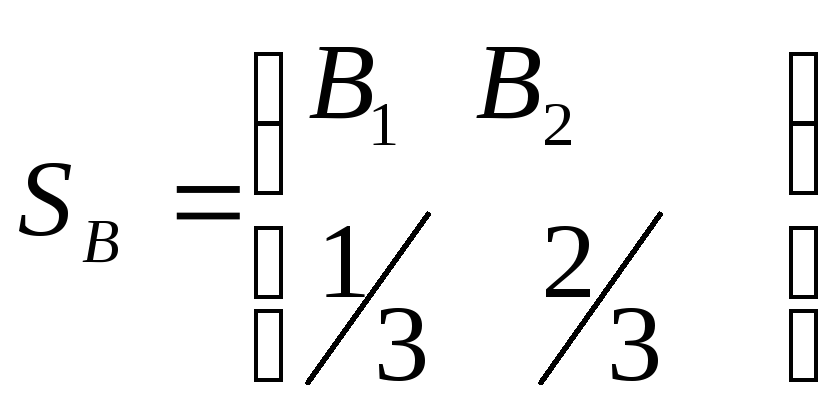цена игры ν = 8/3 (наименьшее из 8/3 и 10/3 ).