§4. Графический способ решения игры .
Решение игры 2x2
допускает наглядную геометрическую
интерпретацию. Пусть игра задана
платежной матрицей P=(аij)
,i,j=1,2
. По оси абсцисс (рис.4.1) отложим единичный
отрезок A1A2
; точка
А1(х=0)
изображает стратегию А1
, а все
промежуточные точки этого отрезка
— смешанные стратегии SA
первого игрока, причем расстояние
от SA
до правого конца отрезка — это вероятность
р1
стратегии А1,
расстояние до левого конца — вероятность
р2
стратегии А2.
На перпендикулярных осях I—I
и II—II
откладываем выигрыши при стратегиях
А1
и A2
соответственно. Если 2-й игрок примет
стратегию В1,
то она дает выигрыши а11
и а21 на
осях 1—1 и II—II,
соответствующие стратегиям А1
и А2.
Обозначим эти точки на осях 1—1 и II—II
буквой B1.
Средний выигрыш ν1
соответствующий смешанной стратегии
SA,
определяется по формуле математического
ожидания
и равен ординате точки М1
которая лежит на отрезке В1В1
и имеет абсциссу SA
(рис. 4.1).
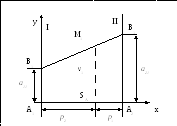
Рис.4.1
Рис.4.2
Аналогично строим
отрезок В2В2,
соответствующий
применению вторым игроком стратегии
В2(рис.4.2).
При этом средний выигрыш
- ордината точки М2.
В соответствии с принципом минимакса оптимальная стратегия S*A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис.4.3), показывает минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке В1N – против стратегии В1, на участке NВ2 – против стратегии В2). Оптимальную стратегию S*A=(p*1 ,p*2) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры ν. На рис.4.3 обозначены так же верхняя и нижняя цены игры α и β.
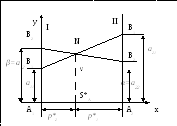
Рис.4.3
Применим геометрический метод для задачи, рассмотренной в примере 2.2.
Пример 4.1. Решить графически игру, заданную платежной матрицей
,
Рис.4.4
Откладываем по оси абсцисс (рис.4.4) единичный отрезок A1A2. На вертикальной оси I—I откладываем отрезки: а11 = 4, соответствующий стратегии В1, и а12 = 2, соответствующий стратегии B2. На вертикальной оси II—II отрезок а21 = 3 соответствует стратегии В1, отрезок а22 = 5 соответствует стратегии B2 (см. рис.4.4). Нижняя цена игры α = а21 = 3 .Верхняя цена игры β = =а11 = 4, седловая точка отсутствует. Из рис.4.4 видно, что абсцисса точки N определяет оптимальную стратегию S*A , а ордината — цену игры ν. Точка N является точкой пересечения прямой В2В2 и В1В1.
Уравнение прямой В1В1 ,проходящей через точки (0; 4) и (1;3):
.
Уравнение прямой В2В2 ,проходящей через точки (0; 2) и (1;5):
Точка пересечения прямых является решением системы:
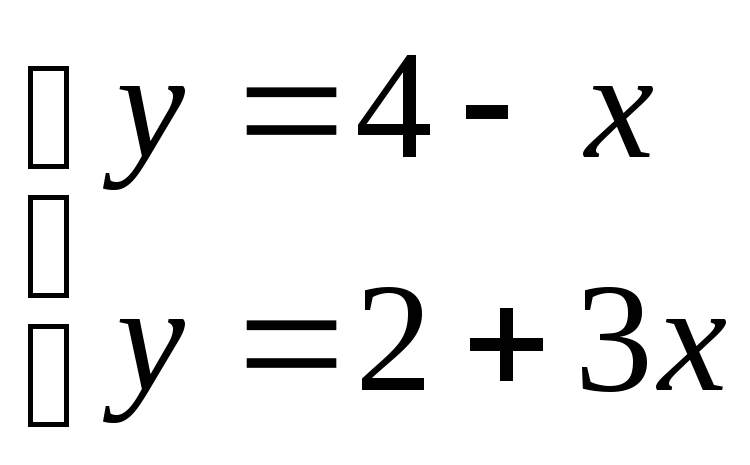
или
х = 1/2, у = 7/2 , т.е. N
(1/2 ;7/2).
Таким образом, p*1 =1/2 ,p*2 =1 - 1/2 = 1/2. Оптимальная стратегия S*A=(1/2 ;1/2), цена игры ν = 7/2.
Геометрически можно также определить оптимальную стратегию игрока В, если поменять местами игроков А и В и вместо максимума нижней границы А2 М А1 в соответствии с принципом минимакса (рис. 4.5) рассмотреть минимум верхней границы.
Рис.4.5
Если платежная матрица содержит отрицательные числа, то для графического решения задачи лучше перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение при этом не изменится, а величина цены увеличится на это число.
При наличии седловой точки графическое решение дают варианты, изображенные на рис.4.6 и 4.7.
На рис.6 наибольшей ординатой на ломаной В1NB2 обладает точка В2, поэтому оптимальной является чистая стратегия А2 для игрока А (В2 – для игрока В), т.е. оптимальное решение S*A=(0 ;1), S*В=(0 ;1). Игра имеет седловую точку а22 =ν.
Чистая стратегия В2 (рис.4.7) не выгодна для игрока В, поскольку при любой стратегии игрока А она дает последнему большой выигрыш, чем чистая стратегия В1. На основании принципа минимакса выделим прямую В1В1 и на ней точку В1 с наибольшей ординатой на оси І-І. Чистая стратегия А2 является оптимальной для игрока А, а чистая стратегия В1 – для игрока В. Оптимальное решение S*A=(0 ;1), S*В=(0 ;1). Игра имеет седловую точку а21=α=β=ν.
Рис.4.6
Рис.4.7