лекция 1 модели

Пример 1. Предположим, что через три года нам понадо­бится 1500 у.е. Спрашивается, сколько средств необходимо вло­жить сейчас, чтобы добиться этого. Так, если известна фиксированная норма прибыли из расчета 8% годовых, т.е. i = 0,08, то отсюда у.е Итак, сейчас необходимо вложить 1190,74 у.е., чтобы через три года получить 1500 у.е. Пример 2. Рассмотрим вложение в 1000 у.е., которое станет 1500 у.е. через пять лет при условии годовой ставки дисконта в 8%. Имеем по формуле: Таким образом, при условии, что ставка дисконта в 8% доста­точно реальна, вложение все же выгодно, хотя, конечно, желатель­но было бы рассмотреть и другие варианты вложений с целью установления, является ли полученное значение чистой дисконти­рованной стоимости оптимальным. Рассмотрим пример выбора наилучшего варианта инвестиро­вания. Пример 3. Пусть ставка сложного процента 6% в год. Рассмот­рим три варианта единовременного вложения определенной суммы. По первому варианту через три года мы будем иметь 1500 у.е., по второму варианту — 1700 у.е. через пять лет и по третьему вариан­ту — 2000 у.е. через семь лет. Эти три варианта нужно сравнить, рас­считав для каждого случая чистую дисконтированную стоимость. Для первого варианта текущая стоимость определяется как : у.е Для второго варианта текущая стоимость равна: у.е Для третьего варианта текущая стоимость составляет: у.е. Следовательно, как это видно из полученных результатов, те­кущая стоимость при третьем варианте выше. Поэтому, исходя из приведенных вычислений, третий вариант вложения кажется более выгодным. Следует отметить, что на практике для опреде­ления наилучшего варианта инвестирования приходится учиты­вать и другие факторы. Пример 4. Первоначальное размещение исходной суммы составило 5000 у.е., после чего в течение пяти лет ежегодно произ­водились регулярные платежи в сумме 500 у.е. При условии годо­вой процентной ставки в 8% стоимость вложения в конце этого периода по формуле равна: у.е. Видно, что исходное вложение в 5000 у.е. за пять лет прирас­тает до 7346,64 у.е., а ежегодные платежи в сумме 500 у.е. прирас­тают до итогового значения в 2933,30 у.е. и общая стоимость вло­жения равна 10279,94 у.е. Изменим условие примера. При размещении начальной сум­мы в 5000 у.е. на вклад под 8% годовых и снятии 500 у.е. в конце каждого года, какая сумма останется на счете через пять лет? Так как периодический платеж есть величина отрицательная, т.е. S = -500 у.е., то окончательная сумма по формуле равна: у.е. Первое слагаемое это сумма, которая могла бы быть на счете через пять лет при исходном вложении в 5000 у.е., а второе слагае­мое включает изъятие со счета за данный период (5 раз по 500 у.е.), а также потери процентного дохода, вызванные изъятием денег. Пример 5. Инвестиционная компания предлагает аннуитет, при котором первоначальный разовый взнос в сумме 15000 у.е. будет приносить по 2000 у.е. в конце каждого года в течение сле­дующих десяти лет. Установите выгодность этого вложения при условии номинальной ставки процента в 8%. Прежде всего определим какова должна быть первоначальная сумма вложения для последующего получения частичных плате­жей по 2000 у.е. По формуле при S_H = 0, так как через десять лет вложения закончатся, имеем: , Отсюда Р = 13419,69 у.е. Таким образом, аннуитет стоит разового взноса в сумме 13419,69 у.е., и при условии сохранения ставки процента на за­данном уровне представляется неудачным вложением. Если же учесть и другие факторы, например, инфляцию, то ясно, что это рисковое вложение капитала, заранее ведущее к потерям. Пример 6. Финансовый рынок по стоимости состоит из 20% безрисковых и 80% рисковых бумаг. Рисковых бумаг четыре типа: первые составляют 1/6 часть и для них = 0,9, вторые — 1/4 часть и = 0,7, третьи —1/3 часть и = 1,1. Найти долю и четвертых бумаг. Найти эффективности всех рисковых бумаг и среднюю доходность по всему рынку, если эффективность рынка (сред­няя доходность по рисковым бумагам) 8%, а безрисковая ставка равна 4%. Доля четвертых бумаг равна β четвертых бумаг находится из условия, что для рыночного пор­тфеля β = 1. Следовательно, отсюда = 37/30. Эффективность каждой ценной бумаги равна: = Тогда Средняя доходность по всему рынку равна: 0,2 • 4 + 0,8 • 8 = 7,2%. При положительной коррелированности актива с рынком, чем больше вносимый рынком риск, тем больше ставка доходности, тем меньше современная оценка будущих доходов от акции и, наоборот, при отрицательной коррелированности актива с рын­ком, чем больше рыночной риск, тем больше современная оценка будущих доходов от актива. Пример 7. Обработка статистических данных показала, что запросы кредитов в банке следующие: 15% — государственные органы, 25% — другие банки и остальные юридические лица. Ве­роятность невозврата взятого кредита соответственно такова: 0,03; 0,06 и 0,15. Найдем вероятность невозврата очередного запроса на кре­дит по формуле полной вероятности. Если — запрос поступил от госорганов, — от банка, — от юридического лица и А — невозврат очередного кредита, то: После сообщения о невозврате кредита, было установлено, что данные клиента в факсе нечеткие. Какова вероятность, что дан­ный кредит не возвращает какой-то госорган? По формуле Байеса имеем: Пример 8. Кредит в сумме 100000 у.е. выдан на пять лет по ставке 12% годовых. Проценты на кредит должны выплачиваться в конце каждого полугодия. Найти необходимую величину выплат в фонд погашения долга, если проценты на выплаты начисляются по ставке 8% годовых. Каким будет размер фонда к концу третьего года? Решение. Проценты на выплаты фонда начисляются по ставке 8% годовых или 4% полугодовых, поэтому, чтобы к концу пятого года фонд содержал 100000 у.е., величина выплат должна быть равна: здесь P_t = 100000 у.е., i = 0,04; п = 10 — число выплат, тогда у.е. Проценты на долг в конце каждого полугодия составляют 6% от 100000 у.е., то есть 6000 у.е. Полный годовой расход по долгу составляет: 8329,1 + 6000 = 14329,1 у.е. В конце третьего года фонд содержит из формулы: = у.е. Ясно, что рассматриваемый способ погашения долга — созда­ние фонда — выгоден должнику только тогда, когда проценты по ставке больше, чем процент выплат за долг. Пример 9. Кредит для покупки товара на 300000 у.е. открыт на три года, процентная ставка — 10%, выплата в конце каждого месяца. Определить ежемесячные платежи. Сумма долга с процентами: = у.е Ежемесячные платежи: ==10833,33 у.е. Пример 10. Кредит в размере 10000 у.е. получен под 12% го­довых. Долг должен быть погашен ежемесячными выплатами в течение года. Найти размер погасительных платежей при равно­мерной выплате процентов. Решение. Если проценты за год обозначим через П, то у.е. у.е. у.е Причем, 833,3 у.е. из каждой выплаты идет на погашение основ­ного долга (10000 у.е.) и 100 у.е. на погашение процентов (1200 у.е.) Подчеркнем еще раз следующий важный момент. Если действи­тельно предполагать, что процентная ставка, по которой выпла­чиваются проценты за пользование кредитом, составляет 12% го­довых, то это глубоко ошибочное предположение, так как эта став­ка намного больше. Нетрудно показать, что при равномерной выплате процентов действительная годовая процентная ставка APR (annual percentage rate) определяется по формуле: = Данная формула включает проценты на невыплаченный оста­ток основного долга. Это значение процента значительно выше предполагае­мых 12%. Пример 11. Потребительский кредит в сумме 10000 у.е. вы­дан на 3 года при разовом начислении процентов по ставке 12% годовых. Погашение задолженности помесячное. Решение. Общая сумма задолженности = у.е. Сумма расходов по обслуживанию долга у.е. Сумма номеров месяцев . Для первого месяца находим: у.е. Если проценты и суммы погашения определять по формуле , то у.е.; Аналогично определяются проценты и суммы погашения дол­га для каждого месяца. Анализ этих результатов показывает, что при равномерном списании долга остаток долга меньше при спи­сании по правилу 78, т.е. равномерное списание приводит к более быстрому списанию задолженности.

Дисциплина: Управленческие решения Билет № 1

1. Значение, сущность и функции решений

2. Психология поведения руководителей в ситуациях риска

3. Задача

От эксплуатации автомобиля предприятие может получать в течение восьми лет прибыль в размере 140 тыс. руб. в год. Определите, какую минимальную сумму должно предприятие получить от продажи данного автомобиля, чтобы в случаи вложения вырученных средств в банк под 15 % годовых на восемь лет иметь прибыль не ниже, чем результат от эксплуатации машины. Остаточная стоимость автомобиля через 8 лет будет равна 100 тыс. руб. Дисциплина: Управленческие решения Билет № 2

1. Интеллектуальная деятельность при разработке решений

2. Меры по снижению возможного риска

3. Задача

Стоимость строительства объекта – 6 млн. руб. Срок строительства – 3 года. Распределение капитальных вложений по годам: I вариант – 1, 2, 3 млн. руб., II вариант – 1,5; 2; 2,5; млн. руб. Найти более экономичный вариант использования капитальных затрат с учетом фактора времени на момент полного окончания строительства. Дисциплина: Управленческие решения Билет № 3

1. Информационное обеспечение решений и информационная безопасность

2. Анализ и оценка последствий риска

3. Задача

Фирме требуется выбрать оптимальную стратегию по обеспечению нового производства оборудованием. Данные для выбора оптимальной стратегии в условиях полной определенности представлены в таблице:

Варианты оборудования (стратегии, решения)	Частные критерии эффективности оборудования*
	производи­тельность, д. е.	стоимость оборудова­ния, д. е.	энергоем­кость, у. е.	надежность, у. е.
Оборудование завода 1,	a11=5	a12=7	a13=5	a14=6
Оборудование завода 2,	a21=3	a22=4	a23=7	a24=3
Оборудование завода 3,	a31=4	a32=6	a33=2	a34=4
* Значения частных критериев даны в условных единицах.

На основе экспертных оценок были также определены веса ча­стных критериев ,: ; ; ; . Определить оптимальную стратегию. Дисциплина: Управленческие решения Билет № 4

1. Сочетание формального и неформального аспектов в разработке решений

2. Риск и его разновидности

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер прибыли в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 5

1. Классификация решений

2. Источники и виды неопределенности

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию

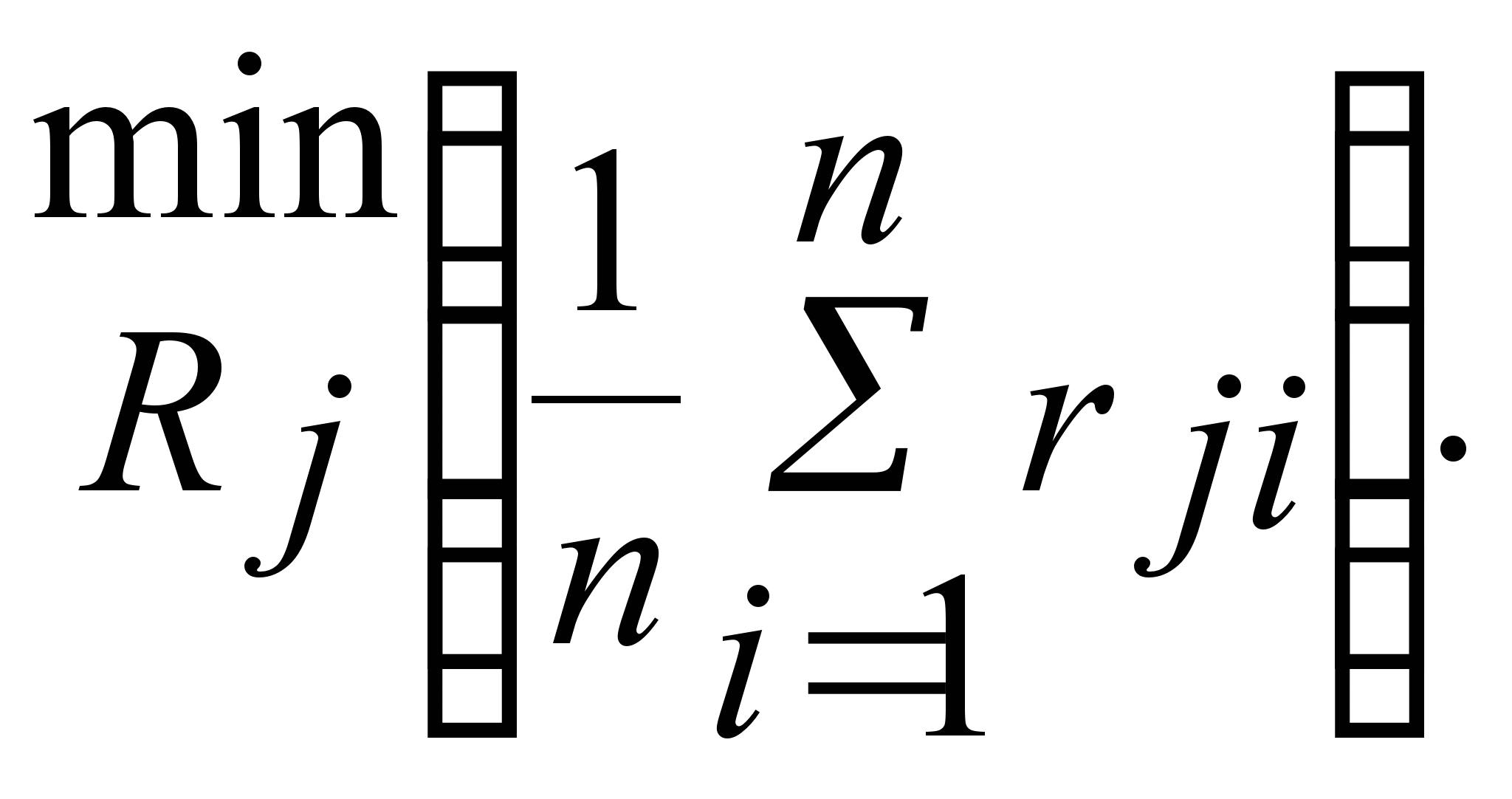
Варианты управленческих решений	Варианты состояния "Природы"
	1	2	3	4
1	5	11	21	25
2	8	6	10	28
3	22	17	16	18
4	26	23	22	16

Дисциплина: Управленческие решения Билет № 6

1. Типология решений

2. Прогнозирование состояния внешней среды

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию

Варианты управленческих решений	Варианты состояния "Природы"
	1	2	3	4
1	5	11	21	25
2	8	6	10	28
3	22	17	16	18
4	26	23	22	16

Дисциплина: Управленческие решения Билет № 7

1. Проблемы и их решение

2. Классификация ситуаций и проблем

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер прибыли в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 8

1. Графическое изображение проблемной ситуации

2. Элементы внутренней среды предприятия

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер затрат в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 9

1. Свойства качественных решений

2. Воздействие факторов внешней среды на функционирование предприятия

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер затрат в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 10

1. Условия и факторы качества решений

2. Расчет параметров сетевого графика

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер прибыли в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 11

1. Организационно-психологические предпосылки качества решений

2. Технология построения сетевых моделей

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер затрат в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 12

1. Технология разработки решений

2. Характеристика сетевых моделей

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер прибыли в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 13

1. Моделирование процесса разработки решения

2. Анализ альтернатив при разработке групповых решений

3. Задача

Определим оптимальную стратегию производства по данным таблицы и предложенному критерию .

Объем производства	Размер затрат в зависимости от колебания спроса
	П1	П2	П3	П4
Р1= 980000	57400	186100	185200	18510
Р2= 1500000	5711	132700	284650	28750
Р3= 1980000	1218	75450	186900	3458

Дисциплина: Управленческие решения Билет № 14

1. Разновидности математических моделей и их использование

2. Сравнение альтернатив и выбор решения

3. Задача

Фирме требуется выбрать оптимальную стратегию по обеспечению нового производства оборудованием. Данные для выбора оптимальной стратегии в условиях полной определенности представлены в таблице:

Варианты оборудования (стратегии, решения)	Частные критерии эффективности оборудования*
	производи­тельность, д. е.	стоимость оборудова­ния, д. е.	энергоем­кость, у. е.	надежность, у. е.
Оборудование завода 1,	a11=5	a12=9	a13=5	a14=8
Оборудование завода 2,	a21=3	a22=6	a23=7	a24=5
Оборудование завода 3,	a31=4	a32=8	a33=2	a34=6
* Значения частных критериев даны в условных единицах.